过焦点的阿基米德三角形的性质及其在高考中的应用

安徽省合肥市第一中学(230601) 谷留明

文[1]介绍了抛物线中阿基米德三角形—-圆锥曲线的弦与过弦端点的两条切线所围成的三角形的一些性质,在此基础上,本问探究圆锥曲线中过一个焦点的阿基米德三角形的统一性质及其逆定理,由此得出圆锥曲线在任意一点处或过准线上任意一点的切线的作图方法,并举例说明了这些性质在解决近几年相关高考题中的妙用.

1 性质定理

性质已知圆锥曲线C的焦点F对应的准线为l,过l上一点P引曲线C的两条切线PA,PB,切点分别为A,B,则直线PF垂直AB于F.

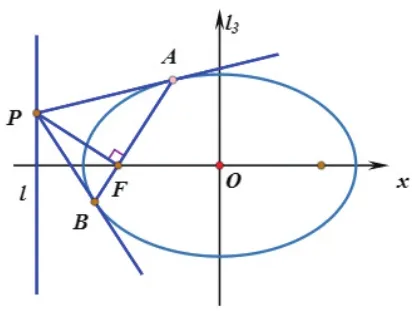
图1

当圆锥曲线C为双曲线时,如图2,证明类似,略.需注意的是,如图3,对于l上的点P,当且仅当P在渐近线上时,过P只能引双曲线C的一条切线.设切点为A,此时易证PF⊥AF于F.

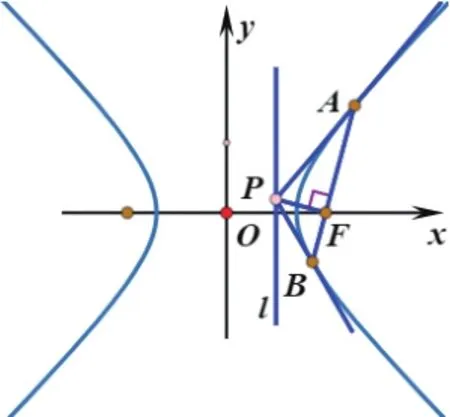
图2

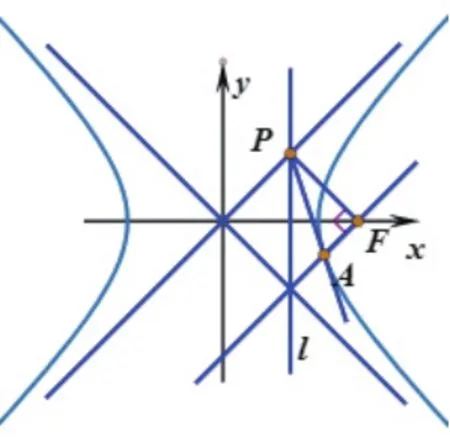
图3

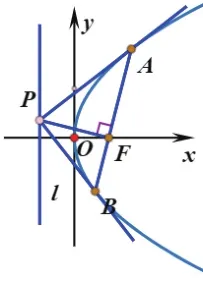
图4

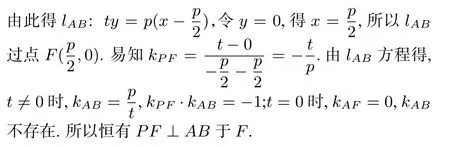
若此性质的条件和结论适当逆过来,命题也成立.

逆定理1已知过圆锥曲线C的一个焦点F的直线交曲线C于点A和B,过F作直线AB的垂线,若垂线与F对应的准线相交于点P,则直线PA,PB均为曲线C的切线.

当圆锥曲线C为双曲线或抛物线时,证明类似,略.

逆定理2已知线段AB为圆锥曲线C的过焦点F的弦,若曲线C在A,B处的切线相交于点P,则点P必在焦点F所对应的准线上,且PF⊥AB.

当m=0时，lAB⊥x轴,kPF=0,PF⊥AB;当0 时,

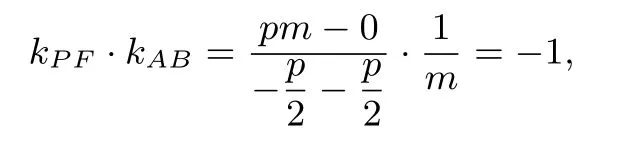
PF⊥AB.

当圆锥曲线C为椭圆或双曲线时,证明类似,略.

进一步研究发现,还有以下结论成立.

结论1已知抛物线C的弦AB过焦点F,抛物线C在A,B处的切线相交于点P,则∠APB=90◦.

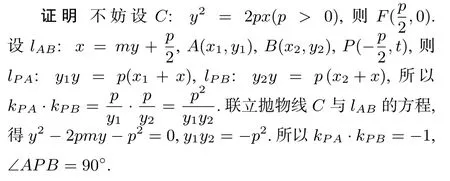
结论2已知抛物线C的弦AB过焦点F,点P在抛物线C的准线上,且∠APB=90◦,则PF⊥AB,且直线PA,PB均为抛物线C的切线.

再根据逆定理1,可得直线PA,PB均为抛物线C的切线.

2 切线作图

由性质2,可以得到圆锥曲线在任意一点A处,或者过准线l上任意一点P的切线的作图方法.

2.1 作圆锥曲线C在任意一点A处的切线(设C的一个焦点为F,其对应的准线为l):

(1)连接AF;

(2)过F作AF的垂线,交l于点P;

(3)连接P和A,直线PA即为圆锥曲线C在点A处的切线.

2.2 作圆锥曲线C的过准线l上任意一点P的切线(设准线l对应的焦点为F):

(1)连接PF;

(2)过F作PF的垂线,作出垂线与曲线C的交点(一个或者两个);

(3)连接P和交点,所得直线(一条或者两条)即为圆锥曲线C过点P的切线.

3 考题妙解

例1(2018年高考全国卷Ⅲ理科第16题)已知点M(−1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90◦,则k=____.

分析本题主要考查直线与圆锥曲线的相交关系,考查数学结合和转化化归思想,考查直观想象和数学运算等核心素养.其基本思路是:设过A(x1,y1),B(x2,y2)两点的直线方程为y=k(x−1),将它与抛物线方程联立、消y,可得k2x2−2(k2+2)x+k2=0,由此表示出x1+x2,x1x2,再结合直线方程表示出y1+y2,y1y2,代入整理可求出k.此法的计算量大而易出错.

而根据结论2,设C的焦点为F,则MF⊥AB.所以轻松得解k=2.

例2(2019年高考全国卷Ⅲ理科第21题第(1)问)已知曲线D为直线上的动点,过D作C的两条切线,切点分别为A,B.(1)证明：直线AB过定点.

分析由性质定理直接可知,定点为C的焦点.证明方法既可以用上文中性质定理的证明方法,也可以直接验证C的焦点坐标恒符合直线AB的方程.

若对性质定理中的条件进行推广,比如过与圆锥曲线C相离的直线l上任一点,甚至过圆锥曲线C外任一点,引曲线C的两条切线,又会有何规律与结论呢?可进行更深的研究.