“四翼”中的综合性—-以2019年高考数学全国卷 III (理)为例

四川省成都市玉林中学(610041) 周先华 吴智敏

《中国高考评价体系》(2019年11月出版)(下面简称为《体系》)中,明确构建了“一核”“四层”“四翼”用于指导高考改革与高考命题工作的测评体系.其中,“四翼”是“素质教育的评价维度在高考中的体现”,是回答“怎么考”的问题,是考查的要求,它分成四个层次,即“基础性、综合性、应用性、创新性”.《体系》的出台,既是对历年高考的总结,也是对2017年颁布实施的《普通高中学科课程标准》中提出的立德树人、培育学科核心素养这一目标的测试与评价.而2019年的高考,恰好处在前后过渡的这样一个特殊时期.下面以2019年高考数学全国3卷(理)为例,来分析《体系》中“四翼”中的综合性在高考数学试题的命制过程中所体现出来的本质特征、显现方式及具体内容.

2019年,习近平总书记在全国教育大会指出,要努力构建德智体美劳全面培养的教育体系,其基本要求就是对学生综合素质的培养.综合素质是一个人的知识水平、道德修养以及各种能力等方面的综合素养.显然,具备良好综合素质的人,才可能在高考考场上综合运用数学知识和数学思想与方法,融会贯通,高质量地解决高考试卷中的那些来自于生活实践或学习探索中的复杂的情境问题.

当然,在一套试题中,基础性试题和综合性试题不是绝对的,甚至在个别试题中,可能有两者的交叉与融合.从近3年高考全国数学卷来看,综合性试题基本上维持在50%.以2019年全国高考卷Ⅲ理科为例,10-12题、15-16题、18题第(2)问、19-21题、22题第(2)问以及23题第(2)问.共计67分,占整套试卷分值的44.7%.如果说基础性试题是高考考生必得分的试题的话,那么综合性试题就是拉开考生之间差距的试题.因为综合性是体现高考在“核心价值引领下对知识的交叉、能力的复合、素养的整合的全方面考查”.

一、综合性的本质特点

1 数学内容的结构化

结构,就是各个组成部分的搭配和排列.对数学内容的结构化的认识,首先应该是能够理解和构建相关数学知识之间的联系.事物的联系是普遍存在的、多种多样的.因为任何事物的内部不同的部分和要素是相互联系的,同时,任何事物都不可能孤立存在,都同其他事物处于一定的相互联系之中,甚至整个世界是相互联系的统一的整体.因此,需要把大量的数学知识进行有序化的组合,以整合成数学内容的结构与体系.打个比方,你一定见过这样的人:对某个领域非常精通,无论问他什么问题,他都能从你的话题切入,旁征博引,将大量的原理、机制、知识点······娓娓道来,清晰而严谨.这就是结构—-在他脑海中,所有的知识点都链接在一起.他知道某一个知识点“应该放在哪里”,也知道“它会通向何方”.如果说碎片化的知识是一张张街景的速写,那知识结构与体系就是一副完整的地图.高考强调试题的综合性,就是强调学生能融会贯通,就是要求学生能把各基础知识之间、各模块之间甚至各学科内容之间进行融合;同时,综合性还要求能够把这些知识与关键能力、学科素养和核心价值之间紧密联系.

例 1(2019年高考全国卷Ⅲ理科第 12题)设函数已知f(x)在 [0,2π]有且仅有5个零点,下述四个结论:

①f(x)在(0,2π)有且仅有3个极大值点

②f(x)在(0,2π)有且仅有2个极小值点

③f(x)在单调递增

④ω的取值范围是

其中所有正确结论的编号是

A.①④ B.②③ C.①②③ D.①③④

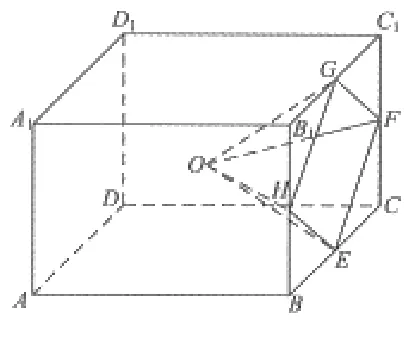
图1

例2(2019年高考全国卷Ⅲ理科第16题)学生到工厂劳动实践,利用3D打印技术制作模型.如图1,该模型为长方体ABCD−A1B1C1D1挖去四棱锥O−EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm,3D打印所用原料密度为0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为___g.

例1考查正弦型函数的周期性、单调性、零点、极值和函数图像,需要学生对正弦型函数的相关知识结构非常熟练.同时,考查数学抽象、逻辑推理、数学运算、直观想象和数学建模等数学学科核心素养,是一道综合能力要求较高的试题.

例2考查求长方体、四棱锥的体积,并根据其体积与密度求出质量.不仅考查多种凸多面体的体积的计算,还考查跨数学与物理学科进行知识整合的能力.

2 问题情境的复杂化

根据问题情境的复杂程度,《体系》中把情境分为两个层次:第一层是简单的情境,第二层是复杂的情境.其中,简单的情境,可以是在解决数学问题时只需运用某一个数学知识点或某一种数学基本能力.

而复杂的情境,可以是在解决问题时需要同时运用一个知识板块内部的几个知识点,或者某几个知识板块中各需要一个甚至多个知识点,或者既需要运用几个知识点,同时还需要运用某一种或几种数学基本能力.

例3(2019年高考全国卷Ⅲ理科第21题)已知曲线为直线上的动点,过D作C的两条切线,切点分别为A,B.

(1)证明:直线AB过定点;

本试题考查抛物线的几何性质、直线与曲线相切、直线过定点等问题.考查数学抽象、逻辑推理、数学建模、数学运算和直观想象等数学学科核心素养.在解决问题过程中,不仅要综合运用抛物线与直线相切(导数或判别式方法)、直线方程的基本形式、直线与曲线相交弦的弦长、点到直线距离、三角形的面积计算等数学知识,还需要运用把直线与曲线位置关系转化为方程组的数形结合思想等.在这样的复杂情境下解决问题,对考生的综合性能力提出了极大的挑战.

二、综合性的呈现形式

1 数学知识的结构与体系

《普通高中数学课程标准(2017年版)》中提出了高中数学课程的三大目标:“四基”和“四能”、发展学生的数学学科核心素养以及提高学生学习数学的兴趣.而实现这些目标的基础是什么?是学生对数学知识的结构与体系的认识和建构.

对高中数学知识的结构与体系的认识,是基于课程标准所规定的课程目标和内容,以及高中学生的学情,要根据高中学生的认知特点,和他们进一步学习数学的需要,并有利于促进学生的未来发展.这样,在教师的引导下,把一些零散的、相对独立的数学概念与规则、数学命题与模型和数学思想与方法等加以整合,使得它们形成具有联系的、动态而相对完善的数学系统,就构成了高中数学的结构与体系.综合性试题就是强调学科内容进行融合,以突显对复合能力的要求.

例4(2019年高考全国卷Ⅲ理科第19题)图2是由矩形ADEB,Rt∆ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=600,将其沿AB,BC折起使得BE与BF重合,连结DG,如图3.

(1)证明:图3中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;

(2)求图3中的二面角B−CG−A的大小.

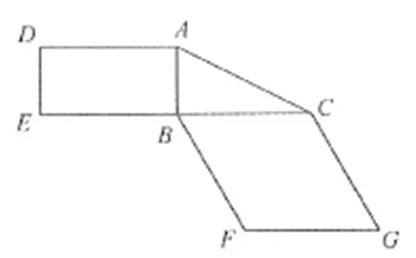
图2

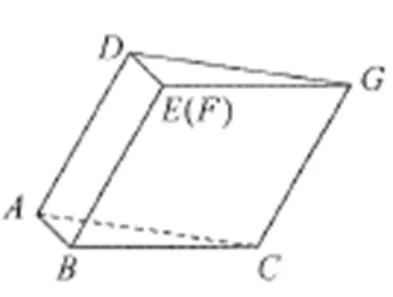
图3

这是一道情境新颖的立体几何考题.首先要对平面图形折叠后再把多个平面粘在一起以构成立体图形.新构成的多面体不是直棱柱,给构建空间直角坐标系带来麻烦;当然,也可以使用传统几何方法,直接通过作辅助线构建二面角的平面角,从而把求二面角转化为解直角三角形,从数学运算角度反而比空间向量方法简洁得多.所以,对平面几何、立体几何和空间向量等相关知识的结构与体系的认知是解决本题的关键.

2 解决问题的思想与方法

数学思想是指由数学学科专家基于数学知识和数学内在规律与特点,经过高度概括和提炼而成的重要思想、观念和见解,而这些思想对数学学习以及以后的发展都具有重要的影响力.数学思想对数学方法起调控作用,而数学方法则是数学思想的外在体现,很多数学方法体现着一定的数学思想.因此很多情况下“思想”与“方法”是等同的,并无十分明确的界限,我们常常笼统地使用“数学思想方法”一词.如何在高中数学课堂上最大化地发展学生数学学科核心素养,启发学生思考,引导学生把握数学内容的本质,从而更加深度地改进教学,还应该着眼于数学思想方法的培育.而综合性试题的一个很重要的目标,就是要对考生在解决数学问题的过程中所蕴含的数学思想与方法的理解与运用水平进行测量与评价.

例5(2019年高考全国卷Ⅲ理科第20题)已知函数f(x)=2x3−ax2+b.

(1)讨论f(x)的单调性;

(2)是否存在a,b,使得f(x)在区间[0,1]上的最小值为−1且最大值为1?若存在,求出a,b的所有值;若不存在,说明理由.

例6(2019年高考全国卷Ⅲ理科第11题)设f(x)是定义域为R的偶函数,且在(0,+∞)单调递减,则( )

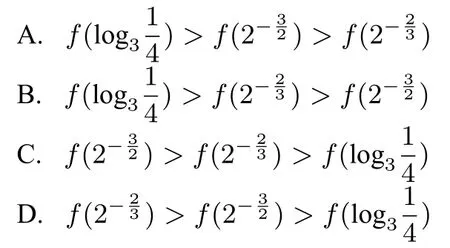
例5涉及的知识主要是导数的应用.第(1)问考查能否准确按导函数的零点大小进行分类讨论;而第(2)问,不仅讨论导函数的两个零点的大小,还要讨论它们和定义域的端点的大小比较.从数学思想方法上看,解决本题的核心就是正确运用分类讨论思想.而考生的易错点也恰好是分类讨论不完全、讨论的依据不明显等.

而例6考查函数基本性质,考生需要运用转化与化归的数学思想,把大小比较问题这个代数问题转化为分析函数图像这个几何问题,即数形结合思想.

三、综合性的主要内容

从数学学科内容的选择角度来看,综合性要求“以多项相互关联的活动组成的复杂情境作为载体,能够反映学科知识、能力内部的整合及其综合运用,体现对即将进入高等学校的学习者的知识、能力、素养之间的纵向整合能力以及综合运用水平的测量与评价”.

从高考评价体系中规定的考查内容上看,必备知识、关键能力、学科素养和核心价值这“四层”是紧密联系的,它们构成一个有机的整体,从而得以“让素质教育的目标在高考中得到系统的体现”.知识、能力与素养虽然各自构成一个完美的系统,但是,不可能有脱离了知识的能力,也不可能有脱离了知识和能力的素养.显然,高素质的人才,必然不仅在知识上有极广的积累,而且在能力与素养上也有着较高的水平.综合性试题必然会考查知识、能力与素养之间的纵向融合能力.

例7(2019年高考全国卷Ⅲ理科第15题)设F1,F2为椭圆的两个焦点,M为C上一点且在第一象限.若∆MF1F2为等腰三角形,则M的坐标为____.

从知识层面上看,本题考查椭圆中的相关概念、椭圆的标准方程及解斜三角形等;从能力层面上看,考查语言解码能力、符号理解能力,信息整理能力、信息转化能力、形象思维和抽象思维能力以及辩证思维能力;从素养层面上看,考查数学抽象、直观想象、逻辑推理、数学运算等数学学科核心素养.

总之,如何体现在核心价值引领下对知识的交叉、能力的复合、素养的整合的全方位的考查,是“四翼”的综合性对高考试题提出的要求.