“等比数列通项公式的应用”的教学新设计

广东省广州市华南师范大学 王嘉乐 何小亚

一、教材分析

基于“不同的学生学习不同的数学”这一理念,对于重点中学的学生,可以把人教版《普通高中课程标准实验教科书 数学(A版)》必修五第二章第四节两节课的内容压缩为第一节课,第二节课的内容改为“等比数列通项公式的应用”这一深化拓展的内容,通过汉诺塔游戏问题来引入等比数列的通项公式的应用.

作为继等差数列后又一特殊的数列,等比数列是研究复杂数列的重要数学模型,与实际生活有密切的联系,如细胞分裂、银行贷款等问题都要用等比数列的知识来解决.本节课的安排可使学生充分参与探索过程,体会等比数列在实际生活中的广泛应用;作为高中阶段培养学生数学推理的重要载体之一,等比数列的应用对培养学生思维的灵活性和创造性以及数学思想的渗透起着重要的作用.

二、学情分析

1.授课对象重点中学的学生.

2.认知基础学生已经掌握了等比数列的定义及通项公式的相关知识,并通过课前预习具备了理解等比数列通项公式的应用的基础,以及接受理解一般化和化归思想的能力.

3.认知障碍(1)将问题a64=?一般化为问题an=?;

(2)递推关系an=2an−1+1的发现;

(3)由递推关系得出等比数列bn.

三、教学目标

1.知识与技能

掌握利用待定系数法求一阶齐次线性递归数列的通项公式的方法.

2.过程与方法

(1)让学生经历“实际问题——数学问题——数学模型——递推关系——解决问题”的过程,积累水平数学化和垂直数学化的经验,培养学生动手实践、提出问题、分析问题和解决问题的能力;

(2)通过把特殊问题a64=?一般化为问题an=?及其探究过程,学习一般化和特殊化的思想;

(3)通过递推关系an=2an−1+1的发现及等比数列的转化过程,学习化归的数学思想.

3.情感态度价值观

(1)通过实验操作探索数学模型,激发学生的好奇心和求知欲,培养学生勇于探索的精神,感受数学探究的乐趣;

(2)通过汉诺塔问题解决的学习,体会到追求简单化是数学的灵魂,并领悟到“数学源于实际,应用于实际,并高于实际”这一真谛!

四、教学重点、难点和关键

1.教学重点(1)“汉诺塔问题”的解决;(2)等比数列通项公式的应用.

2.教学难点(1)递推关系an=2an−1+1的发现;(2)由递推关系an=2an−1+1求解通项公式.

3.突破难点的关键(1)暂时将第n个盘子忽略,从而将问题化为个盘子的问题;(2)根据等比数列核心结构——乘法结构,考虑将递推关系an=2an−1+1的等式右边转化为乘积的形式.

五、教学方法与手段

1.教学方法本节课并不是按照一般的“先讲知识,再讲知识的高考应用”这种方式进行教学,而是采用问题解决教学法,即:“实际问题——数学问题——数学模型——递推关系——解决问题”,充分发挥教师的主导作用和学生的主体作用,学生不再是被动的知识接受者,而是问题解决的主人.

2.教学手段问题驱动,动手实验,分析思考,板书、多媒体手段相结合.

六、教学流程设计

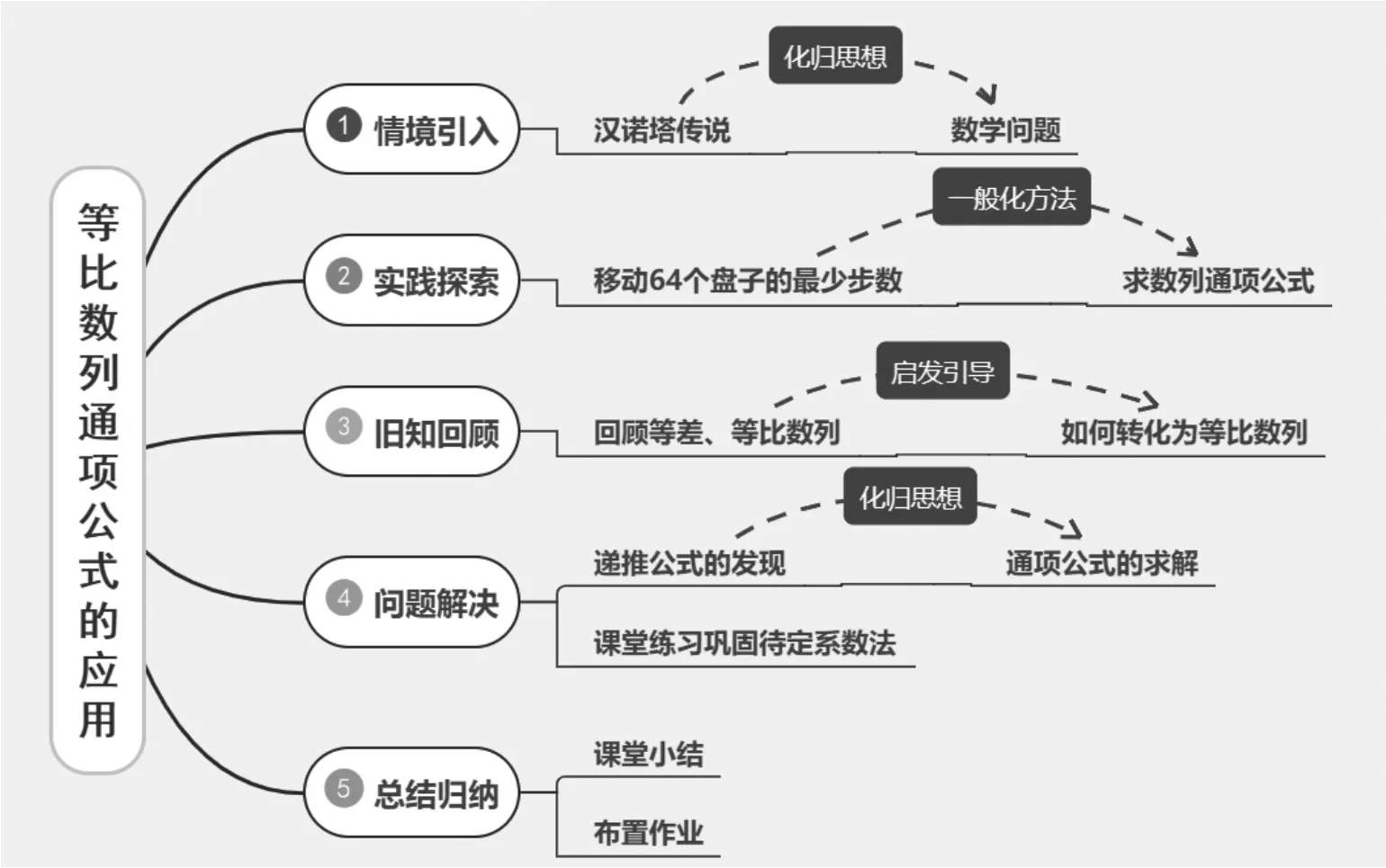
七、教学过程

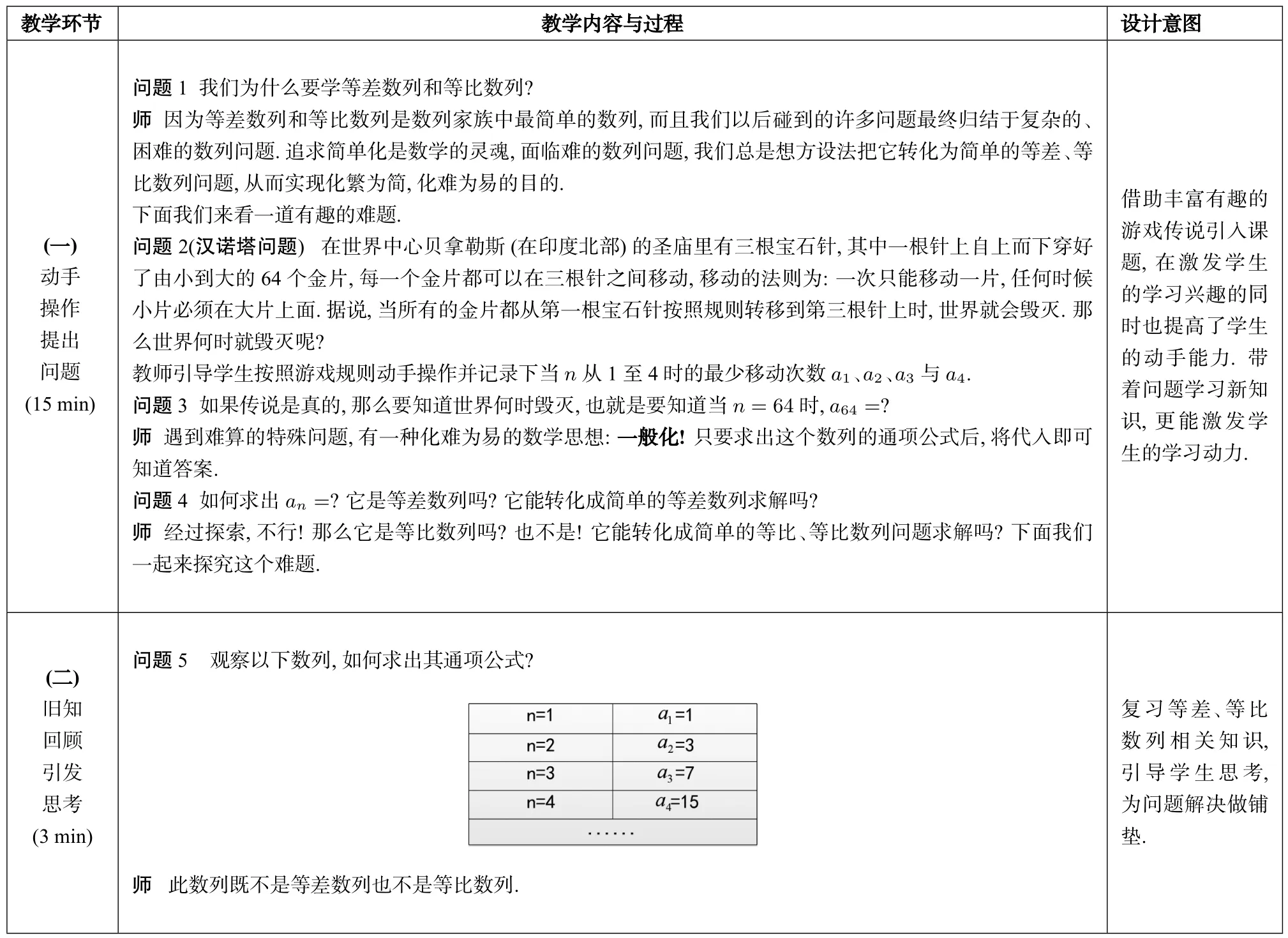
_教学环____________________________________________节教学内容与过程__________________________________________设计意图_______(一)动手操作提出问题(15 min)问题1我们为什么要学等差数列和等比数列?师 因为等差数列和等比数列是数列家族中最简单的数列,而且我们以后碰到的许多问题最终归结于复杂的、困难的数列问题.追求简单化是数学的灵魂,面临难的数列问题,我们总是想方设法把它转化为简单的等差、等比数列问题,从而实现化繁为简,化难为易的目的.下面我们来看一道有趣的难题.问题2(汉诺塔问题)在世界中心贝拿勒斯(在印度北部)的圣庙里有三根宝石针,其中一根针上自上而下穿好了由小到大的64个金片,每一个金片都可以在三根针之间移动,移动的法则为:一次只能移动一片,任何时候小片必须在大片上面.据说,当所有的金片都从第一根宝石针按照规则转移到第三根针上时,世界就会毁灭.那么世界何时就毁灭呢?教师引导学生按照游戏规则动手操作并记录下当n从1至4时的最少移动次数a1、a2、a3与a4.问题3如果传说是真的,那么要知道世界何时毁灭,也就是要知道当n=64时,a64=?师 遇到难算的特殊问题,有一种化难为易的数学思想:一般化!只要求出这个数列的通项公式后,将代入即可知道答案.问题4如何求出an=?它是等差数列吗?它能转化成简单的等差数列求解吗?师 经过探索,不行!那么它是等比数列吗?也不是!它能转化成简单的等比、等比数列问题求解吗?下面我们一起来探究这个难题.借助丰富有趣的游戏传说引入课题,在激发学生的学习兴趣的同时也提高了学生的动手能力.带着问题学习新知识,更能激发学生的学习动力.(二)旧知回顾引发思考(3 min)问题5 观察以下数列,如何求出其通项公式?images/BZ_36_960_2747_1412_2972.png复习等差、等比数列相关知识,引导学生思考,为问题解决做铺垫.师 此数列既不是等差数列也不是等比数列.

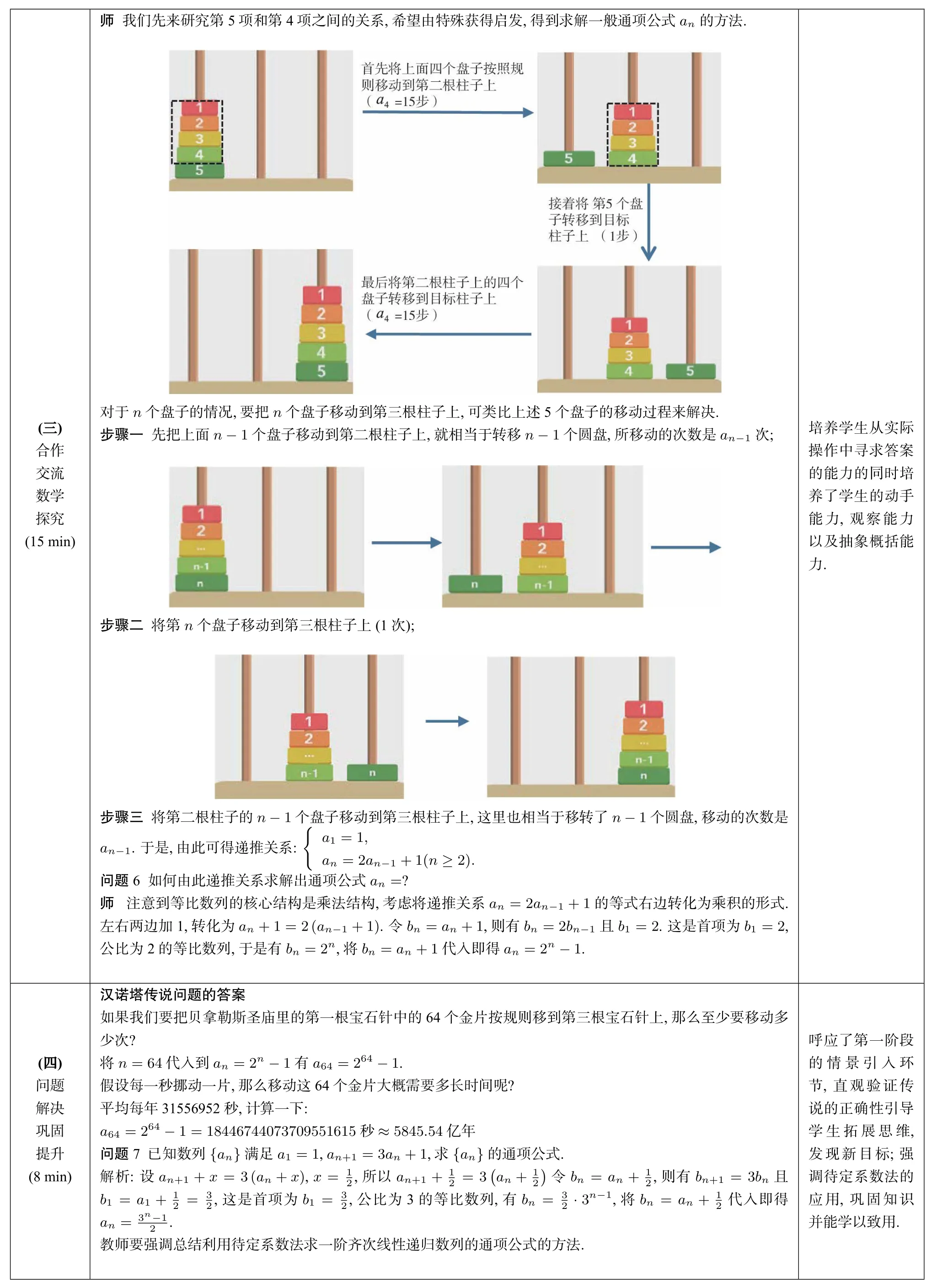
师 我们先来研究第5项和第4项之间的关系,希望由特殊获得启发,得到求解一般通项公式an的方法.(三)合作交流数学探究(15 min)对于n个盘子的情况,要把n个盘子移动到第三根柱子上,可类比上述5个盘子的移动过程来解决.步骤一 先把上面n−1个盘子移动到第二根柱子上,就相当于转移n−1个圆盘,所移动的次数是an−1次;培养学生从实际操作中寻求答案的能力的同时培养了学生的动手能力,观察能力以及抽象概括能力.步骤二 将第n个盘子移动到第三根柱子上(1次);步骤三 将第二根柱子的n−1个盘子移动到第三根柱子上,这里也相当于移转了n−1个圆盘,移动的次数是an−1.于是,由此可得递推关系:{a1=1,an=2an−1+1(n≥2).问题6如何由此递推关系求解出通项公式an=?师 注意到等比数列的核心结构是乘法结构,考虑将递推关系an=2an−1+1的等式右边转化为乘积的形式.左右两边加1,转化为an+1=2(an−1+1).令bn=an+1,则有bn=2bn−1且b1=2.这是首项为b1=2,公比为2的等比数列,于是有bn=2n,将bn=an+1代入即得an=2n−1.(四)问题解决巩固提升(8 min)汉诺塔传说问题的答案如果我们要把贝拿勒斯圣庙里的第一根宝石针中的64个金片按规则移到第三根宝石针上,那么至少要移动多少次?将n=64代入到an=2n−1有a64=264−1.假设每一秒挪动一片,那么移动这64个金片大概需要多长时间呢?平均每年31556952秒,计算一下:a64=264−1=18446744073709551615秒≈5845.54亿年问题7已知数列{an}满足a1=1,an+1=3an+1,求{an}的通项公式.解析:设an+1+x=3(an+x),x=1 2,则有bn+1=3bn且b1=a1+1 2,所以an+1+12=3(an+12)令bn=an+1 an=3n−1 2=32,这是首项为b1=32,公比为3的等比数列,有bn=32·3n−1,将bn=an+12代入即得2.教师要强调总结利用待定系数法求一阶齐次线性递归数列的通项公式的方法.呼应了第一阶段的情景引入环节,直观验证传说的正确性引导学生拓展思维,发现新目标;强调待定系数法的应用,巩固知识并能学以致用.

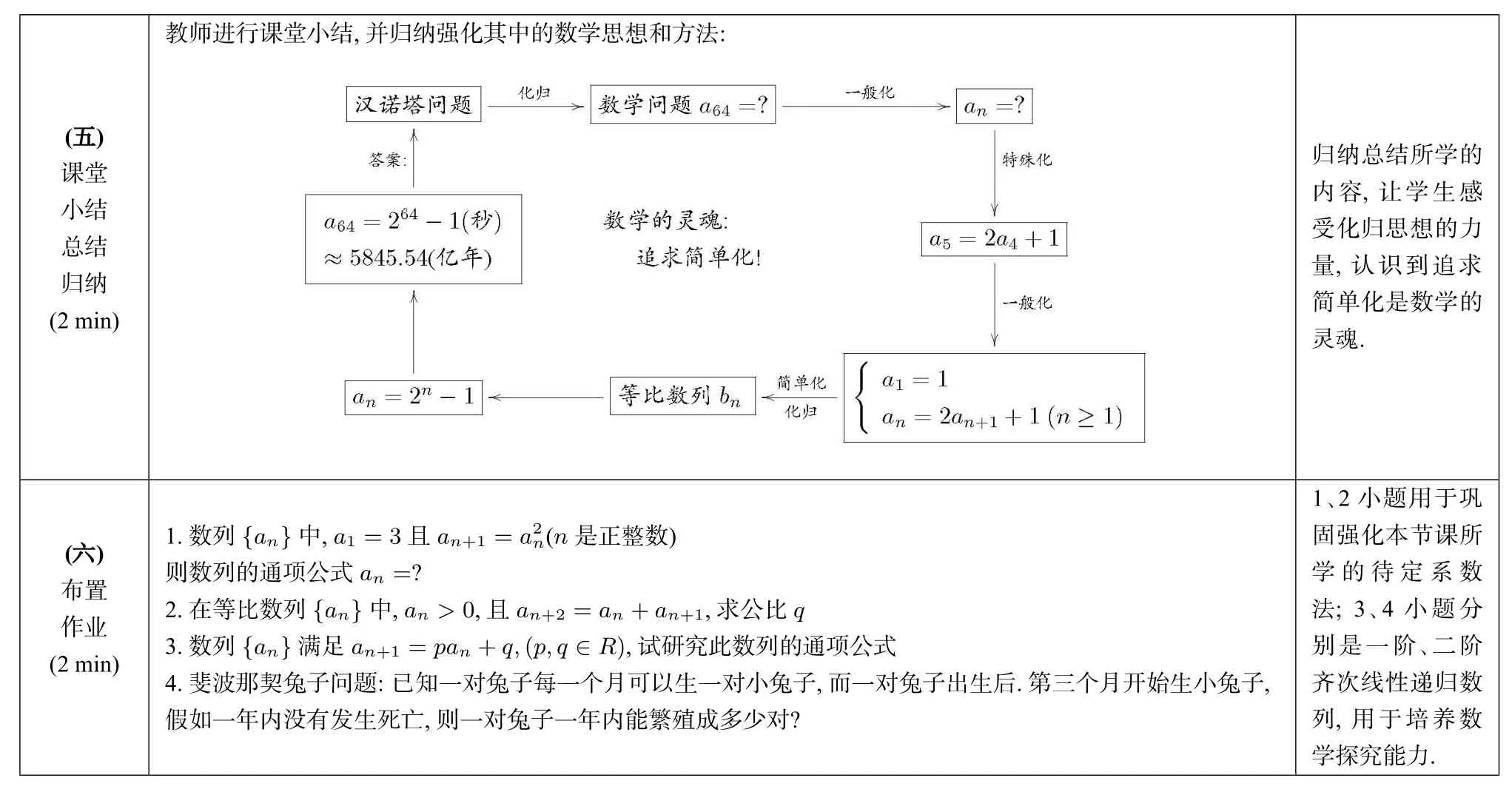
教师进行课堂小结,并归纳强化其中的数学思想和方法:(五)课堂小结总结归纳(2 min)归纳总结所学的内容,让学生感受化归思想的力量,认识到追求简单化是数学的灵魂.(六)布置作业(2 min)1.数列{an}中,a1=3且an+1=a2n(n是正整数)则数列的通项公式an=?2.在等比数列{an}中,an＞0,且an+2=an+an+1,求公比q3.数列{an}满足an+1=pan+q,(p,q∈R),试研究此数列的通项公式4.斐波那契兔子问题:已知一对兔子每一个月可以生一对小兔子,而一对兔子出生后.第三个月开始生小兔子,假如一年内没有发生死亡,则一对兔子一年内能繁殖成多少对?1、2小题用于巩固强化本节课所学的待定系数法;3、4小题分别是一阶、二阶齐次线性递归数列,用于培养数____________________________________________________________________________________________________________________________________________________________________________________________________________________________________学探究能力.

八、本教学设计的特色

1.因材施教上的特色

教材中并没有设置本节课的内容,本教案突破了教材的限制,为重点中学的学生而设计,体现了不同学生学不同的数学和接受不同的数学教育的新课程理念.

2.教法上的特色

本节课并不是按照一般的“先讲知识,再讲知识的高考应用”这种方式进行教学,而是基于问题解决的需要而引入数学新模型,即递推关系,体现了追求问题解决的国际数学教育价值取向.

3.落实数学思想和数学建模素养的特色

通过汉诺塔问题解决过程,使学生积累了数学化(mathematiczation)的经验,提高其数学建模素养;通过把特殊问题a64=?一般化为问题an=?,通过递推关系an=2an−1+1的发现及等比数列的转化等过程,渗透特殊化、一般化和化归的数学思想,并将“追求简单化”这一数学灵魂贯穿始终,体现了数学核心素养教育的要求.

致谢感谢华南师范大学数学科学学院冯伟贞教授对本文的指导.