三角形“四心”平面向量统一表征

广东省广州市第十六中学(510080) 温伙其

平面向量是高中数学重要基本工具之一,它是实现代数与几何相互转化的桥梁.而三角形的内心、外心、重心、垂心具有很多特殊性质.当平面向量和三角形“四心”结合时,则有以下两个优美结论,也称“奔驰定理”.

命题1若点P为∆ABC内一点,总有

证明文[1]已经给出了一种证明方法,除此方法外也可借助法向量给予证明.下面再通过向量形式定比分点公式给予证明.如图1,延长AP交BC于点D,由向量形式定比分点公式有

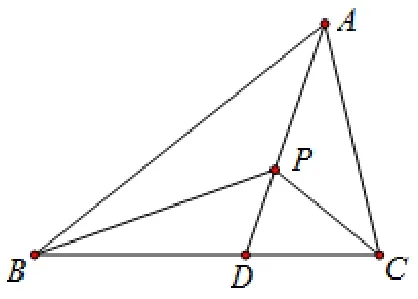
图1

借助上述两个重要结论以及三角形“四心”的定义,我们可以证明三角形“四心”下面四组优美的统一表示:

一、三角形“四心”的平面向量运算表征

当点M、N、P、H分别为∆ABC(非直角三角形)的内心、外心、重心、垂心时,分别有以下关系式成立:

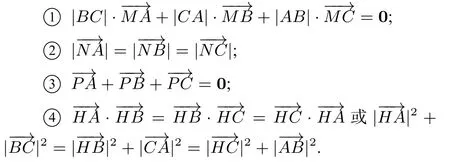
三角形三个内角平分线的交点为内心;三条边中垂线的交点为外心;三条中线的交点为重心;三条高线的交点为垂心.根据这些定义容易证明上述表征.

二、三角形“四心”的三角函数表征

当点M、N、H分别为∆ABC(非直角三角形)的内心、外心、垂心时,分别有以下关系式成立:

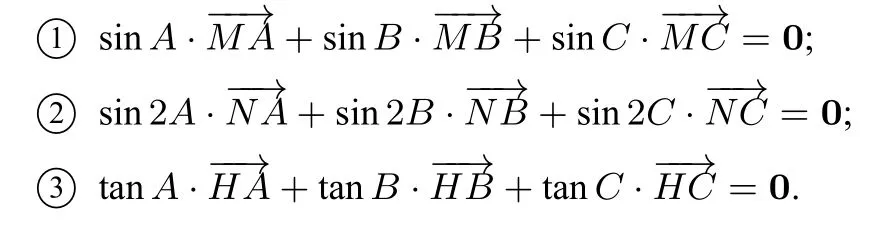
证明对于①,如图2,当点M是∆ABC的内心时,设内切圆半径为r,则有

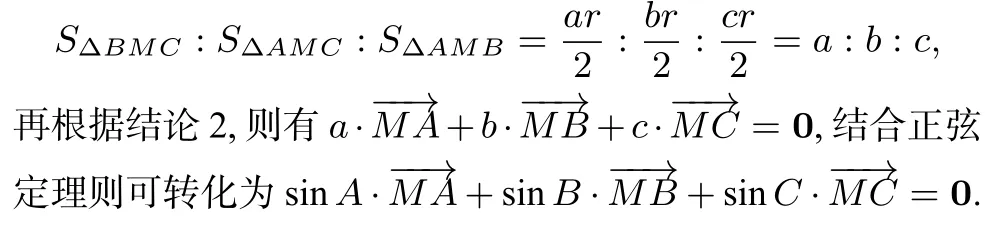
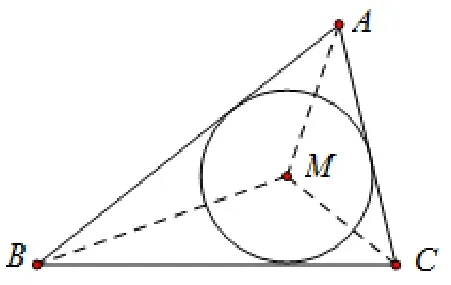
图2

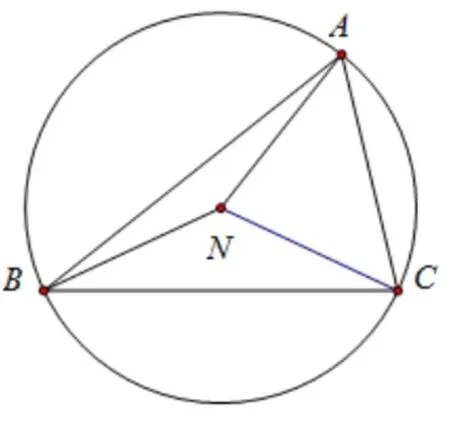
图3

对于③,如图4,当点H是∆ABC(非直角三角形)的垂心时,有S∆BHC:S∆AHC:S∆ANB=tanA:tanB:tanC,再根据结论2,则有

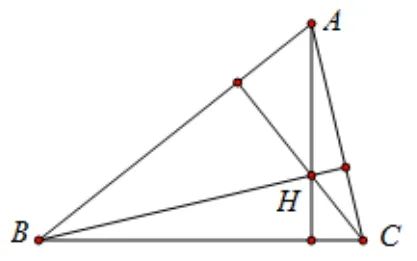
图4

三、三角形“四心”的单位向量表征

已知O为平面上的一个定点,A、B、C是该平面上不共线的三个动点,

四、三角形“四心”的正余弦定理表征

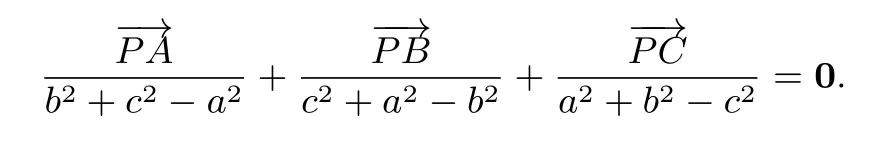
三角形“四心”虽然产生来源不同,反映的几何特征也各自不同,在平面向量工具的背景下,我们总结归纳得到上述优美的表示.四组平面向量表示可依次称为“向量运算表征”、“三角函数表征”、“单位向量表征”和“正余弦定理表征”.从而,三角形“四心”的表示,得到丰富的呈现,也得到优美的和谐统一.