巧作辅助线妙解圆问题

2020-05-22 05:14

在中学阶段,同学们学习了圆的定义、圆的性质、圆的数学规律,在进行圆知识的习题训练中,常遇到一些看上去无法下手的问题,此时如果能够熟练应用圆的半径、直径、切线等,灵活根据需要适当添加一些辅助线,往往就会有“豁然开朗”的感觉。下面举例说明。

一、作半径构造等腰三角形

求解圆的边角关系问题时,通过作圆的半径,可以利用“同圆的半径相等”构造等腰三角形,从而把看上去毫无关联的线段、角的问题转化到等腰三角形中,利用三角形的边角关系进行解答。

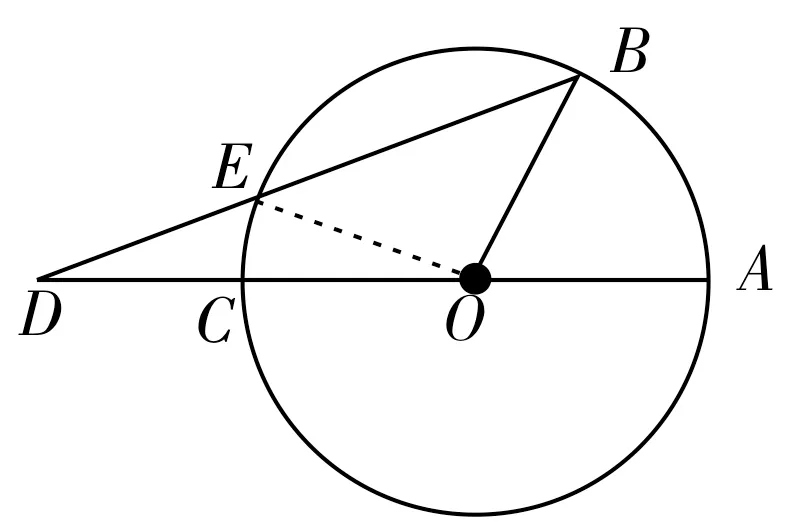
图1

例1如图1 所示,已知AC是⊙O的直径,点B在圆周上(不与点A、C重合),点D在AC的延长线上,连接BD交⊙O于点E。若∠AOB=3∠D。求证：DE=OB。

证明：连接EO,因为∠AOB=∠D+∠B,∠AOB=3∠D,所以∠B=2∠D。因为OB=OE,所以∠OEB=∠B。因为∠OEB= ∠DOE+ ∠D,所以∠DOE=∠D,所以DE=OE。因为OE=OB,所以DE=OB。

评析：本题通过先作辅助线半径OE,构造出等腰三角形OBE,然后利用等腰三角形的两底角相等和三角形的外角等于不相邻的两个内角的和的性质,顺利转化了初看毫无关系的线段DE与OB的长度关系。

当所求圆的问题中已有半径或直径时,通过作圆的弦,可以利用“同一条弦所对的圆周角等于圆心角的一半”“直径所对的圆周角是直角”等圆心角与圆周角的特殊性质,顺利求得圆中其他角度的大小等。

例2如图2所示,AB为⊙O的直径,弦CD与AB相交于点E。已知∠ACD=55°,∠ADC= 50°,求∠CEB的度数。

图2

解：连接BD,因为AB为⊙O的直径,所以∠ADB=90°。又因为∠ADC=50°,所以∠CDB=∠ADB- ∠ADC=40°。因为∠CDB与∠CAB是同弧所对的圆周角,所以∠CDB=∠CAB=40°。所以∠CEB= ∠CAB+∠ACD=40°+55°=95°。

评析：本题中有一条直径,要求的是角度,作弦BD,可以利用直径所对的圆周角是直角、同圆中同弧所对的圆心角相等这两个圆心角定理的推论,轻松求得∠CEB的度数。

当所求圆的问题中已有半径和弦时,通过作弦的垂线,可以利用垂径定理及其推论,结合构造出的直角三角形的边角关系,求解线段和角度的大小。

例3已知⊙O的半径为2cm,弦AB为,求弦AB所对应的圆周角。

图3

解：根据题意作⊙O和弦AB,如图3所示,过圆心O作OD⊥AB交AB于点D。在 Rt △AOD中,有sin∠AOD=sin ∠AOD=所以∠AOD=60°,∠AOB=120°。当弦AB所对的圆周角在优弧上时,有∠AP1B=;当弦AB所对的圆周角在劣弧上时,有∠AP2B=180°-60°=120°。

评析：本题不仅要求同学们能够作出过圆心的弦的垂线这一辅助线,而且要求同学们能够注意到多解问题,难度稍大,要求稍高。