另辟蹊径 柳暗花明——2019年高考数学江苏卷第12题中难点突破的物理思想

■王恩普 高兆梅

历年来的江苏卷很注重对考生综合能力的考查,2019 年高考数学第12 题更是体现了这一特点,下面具体分析。

1.试题呈现

图1

如图1所示,在△ABC中,D是BC的中点,点E在边AB上,BE=2EA,AD与CE交于点O。若的值是_____。

2.思路分析

本题中所求为AB与AC的比值,所以容易想到以AB,AC为基底,条件中的AO,EC只要能够用AB,AC来表示即可,而EC表示很容易,所以主要的问题在于AO的表示。求解此题的思路大概有如下两大类(鉴于本文讨论的方向,只给出AO的表示)。

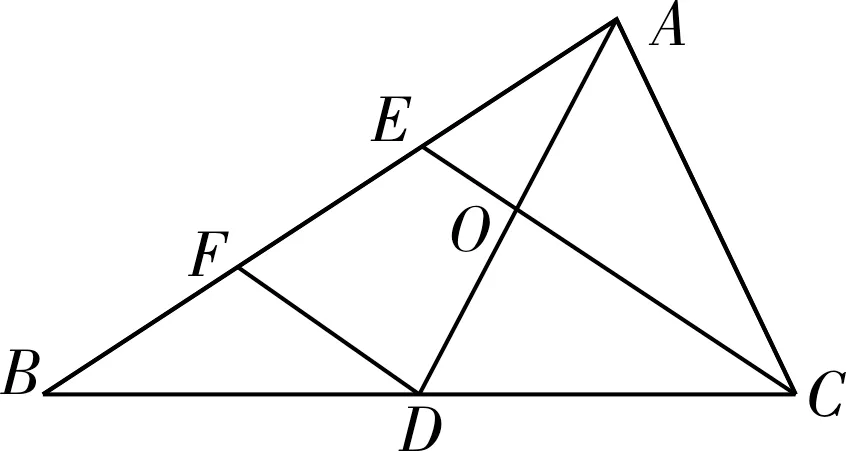
图2

思路1：平面几何。如图2所示,过点D作EC的平 行线交AB于点F,因为D是中点,DF∥EC,则F为BE的中点,而BE=2EA,则有AF=2AE。又EO∥DF,则O是AD的中点,到此AO的表示即可解决。

思路2：共线定理。设则而E,O,C三点共线,则有,到此AO的表示亦可解决。

其实,无论是用平面几何,还是运用共线定理,都是为了解决AO与AD之间的关系,进而把表示出来。但是上面我们也分析了,真正解决这一比例关系是这个问题的难点,下面我们用物理方法来突破这个难点。

3.解法探索

我们先来了解一下物理中的杠杆原理,杠杆平衡原理的数学表达形式为“动力×动力臂=阻力×阻力臂”。应用杠杆平衡原理解决几何线段比值问题,关键在于将图形中的各个交点视为受力点,从而利用两个同向平行力的法则“合力的大小等于两个分力的和,两分力对于以合力作用点为支点的合力矩等于零”,即如图3 所 示,利用F=F1+F2,∑MO=0,或F1·OA=F2·OB来解题。

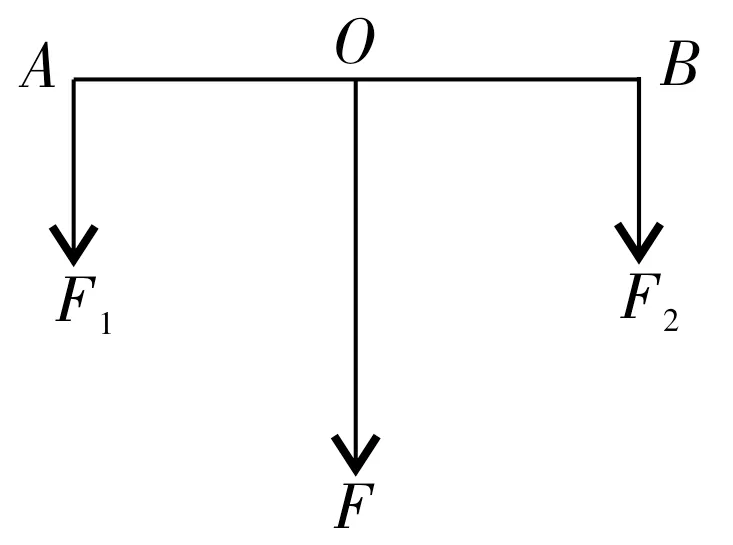
图3

再回到上述提到的2019年高考数学试题中,因为BE=2AE,所以我们把E看成支点,如果在B处挂一个重为1N 的物体,根据杠杆平衡原理,则在A点挂一个重为2N 的物体,杠杆AEB就可以平衡了,此时E点所受合力为1N+2N=3N。同理,由于BD=DC,要保持杠杆BDC平衡,C处要挂一个重为1N 的物体,此时D点所受合力为1N+1N=2N。再看杠杆AOD,因为A,D两点都挂有重为2N 的物体,所以要保持平衡,O点应该是AD的中点,即,到此困扰我们的难点也就随之解决了。

在解答数学问题时,若运用常规思路遇到困难时,同学们可以换个思维,站在数学学科外往往会有不一样的发现,如果可以运用好这一点,同学们的学习能力和解答问题的能力将会得到很大的提升。