例谈由全等到相似

■

中学的平面几何是一个比较复杂的内容,在各种考试中占的比例都很大,是同学们比较头疼的问题。同学们在学习的过程中,要多对题目进行总结归纳、类比迁移,真正理解几何模型及它们的特征,从而达到事半功倍的效果。下面我们来看这样一组例题。

例1已知：△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N。

(1)如图1所示,求证：AE=BD。

(2)如图2所示,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2 中四对全等的三角形。

图1

图2

解：(1)因为△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,所以AC=BC,DC=EC。 所 以 ∠ACB+∠ACD= ∠DCE+ ∠ACD,即∠BCD=∠ACE。 在 △ACE与 △BCD中,所 以△ACE≌△BCD(SAS),所以AE=BD。

(2)由题意得∠ACB=∠DCE,AC=BC,DC=EC。因为AC=DC,所以AC=CD=EC=CB,所 以△ACB≌△DCE(SAS)。由(1)可 知,∠AEC= ∠BDC,∠EAC=∠DBC,所以∠DOM=90°。又因为∠AEC= ∠CAE= ∠CBD,∠ACB=∠DCE,所以∠MCE=∠NCB。又CE=CB,所 以△EMC≌△BNC(ASA),所 以CM=CN,所以DM=AN,所以△AON≌△DOM(AAS)。因为DE=AB,AO=DO,所以Rt△AOB≌Rt△DOE(HL)。

由这个模型还可以得到以下常见结论：∠BOE=90°,OC平分∠BOE,OE=OB。

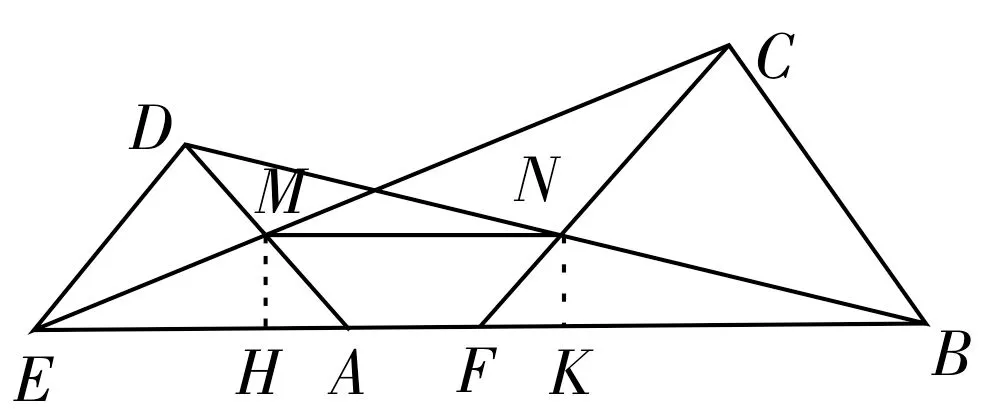
图3

例2如图3所示,△ADE,△FBC为等腰直角三角形,斜边EA,FB在同一直线上,连接BD交FC于点N,连接CE交AD于点M,连接MN。

(1)证明：AM=FN。

(2)证明：MN与BE平行。

证明：(1)因为△ADE,△FBC为等腰直角三角形,所以∠DAE=∠CBE=45°,所以AD∥BC。同理,DE∥CF。所以△AME∽△BCE,△BNF∽△BDE,所以FN=又因为AE= 2DE,BF=2BC,所以AM=FN。

(2)过M作MH⊥AE,NK⊥BE,垂足为H,K。由题意知,∠DAE= ∠CFB=45°, 在△AMH与△FNK中,所以△AMH≌△FNK(AAS),所以MH=NK。因为∠MHA=∠NKB=90°,所以MH∥NK。

两个例题的基本模型都是等腰直角三角形,一个是手拉手共顶点问题,一个是不共顶点问题,一个是全等,一个是相似。共同点是都要用到边和角的等量关系,不同点是等量关系所用的结论不同。

小结：三角形的全等与相似是平面几何的基础,在学习的过程中,有不少同学因为这一部分内容太难而丧失了对数学学习的兴趣。因此,在学习的过程中,同学们要多总结基本题型,多前后对比,提升学习兴趣,提高解决问题的能力。