n维Goodwin模型的全局Hopf分支*

曾小彩，熊佐亮

(1.江西师范高等专科学校 数信学院，江西 鹰潭 335000;2.南昌大学 理学院，南昌 330000)

1 引言

在文献[1]中，研究了以下n维Goodwin模型

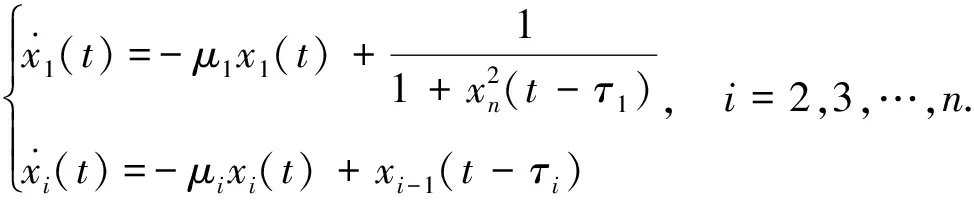
(1)

其中x1(t),xi(t)(i=2,3,…,n)分别表示t时刻mRNA，蛋白质的浓度，τi>0(i=2,3,…,n)表示转录和转译时滞，μi>0(i=2,3,…,n)为动力学常数，对系统(1)详细的解释见文献[1-4].

对于系统(1)，在文献[1]中已经获得了其正平衡点的稳定性和局部Hopf分支的存在性，而关于系统(1)全局Hopf分支的结果尚未讨论和研究.我们知道从局部分支出来的的周期解只是在分支值的小领域内存在，对于局部周期解的延拓即全局周期解是否存在有着重要的实际意义.本文中，我们利用吴建宏等人建立的全局Hopf分支定理研究了系统(1)的全局Hopf分支，并给出了数值模拟以进一步验证我们所得到的结论.有关更多时滞微分方程全局Hopf分支的讨论可见文献[5-7].

证明系统(1)在平衡点E线性部分的特征方程为

λn+P1λn-1+P2λn-2+…+Pn-1λ+Pn+Qe-λτ=0.

(2)

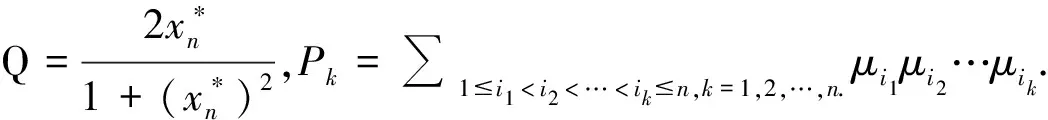
假设λ=iω(ω>0)是方程(2)的根，代入分离实部和虚部，可得

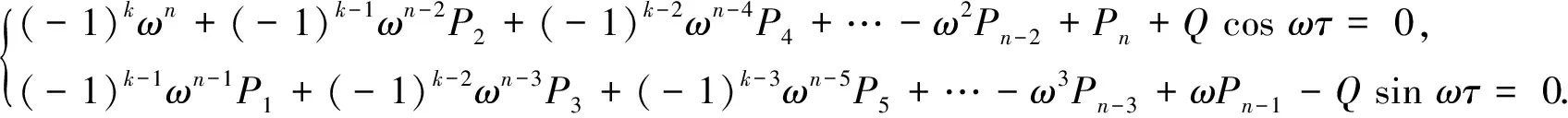
(3)

当n=2k时，有

(4)

当n=2k+1时,(3)式两边平方相加得

ω2n+D2ω2(n-1)+D4ω2(n-2)+…+D2(n-2)ω4+D2(n-1)ω2+D2n=0.

(5)

其中

⋮

H(z)=zn+D2zn-1+D4zn-2+…+D2(n-2)z2+D2(n-1)z+D2n.

(6)

如果D2k>0,k=1,2…,n.可知H(0)=D2n>0.且

H′(z)=nzn-1+(n-1)D2zn-2+(n-2)D4zn-3+…+2D2(n-2)z+D2(n-1).

由于z>0,知方程(5)没有实根，从而方程(2)没有纯虚根.

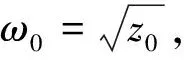
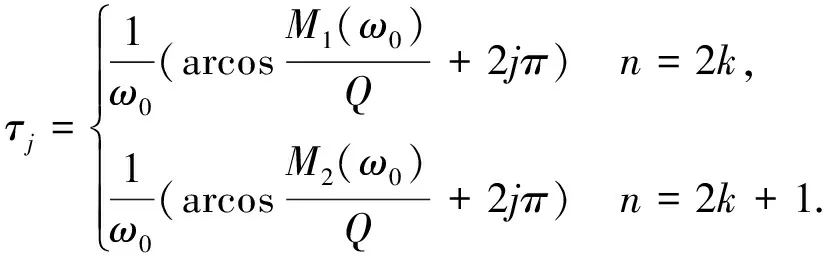
(7)

其中M1(ω)=-[(-1)kωn+(-1)k-1ωn-2P2+…-ω2Pn-2+Pn],

M2(ω)=-[(-1)kωn-1P1+(-1)k-1ωn-3P3+…-ω2Pn-2+Pn].

引理2若D2k>0,k=1,2…,n.且则对所有的τ>0，(2)式没有实根.

引理4对于系统(1)，有如下结论成立：

2 全局Hopf分支分析

由引理4可知，当τ=τj,j=0,1,2,…n时，系统(1)在正平衡点处经历了局部Hopf分支.接下来，我们将利用全局Hopf分支定理研究系统(1)在正平衡点处的由局部Hopf分支延拓的全局周期解的存在性,相关文献[8-9].

目前，正阳县已有300多名农村青年民兵参与“正阳牛”植保服务队，全县共拥有136家“正阳牛”打药分队和287台自走式高地隙打药机械、植保无人机6架，产值达1500万元。2018年累计喷药100多万亩，并承接了2018年正阳县部分小麦条绣病的统防统治工作。从此，牛超打响了“正阳牛”植保服务的品牌。

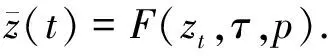
(8)

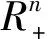
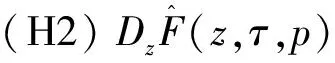
(H3)F(Φ,τ,p)关于Φ是可导的.

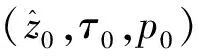
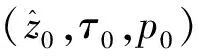
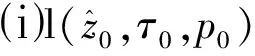
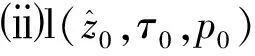
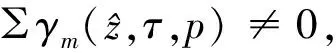
引理6当τ有界时，系统(8)的所有非常数周期解是一致有界的.

证明令x1(t),x2(t),…,xn(t)是(8)的解且定义

其意味着系统(8)的解不能横截穿过x轴和y轴，因此系统(8)的周期轨道必定位于每个象限中.由系统(8)的初值可知，对所有的t≥0,有xi(t)>0(i=1,2,…,n).且有

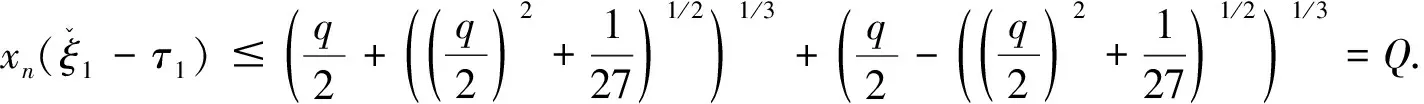
(9)

由(9)式可得q/(1+Q2)≤xn(ξn)≤q,即系统(1)的非常数周期解是一致有界的.

引理7系统(1)没有周期为τ的非常数周期解.

证明假设系统(1)有周期为τ的非常数周期解，则如下系统有非常数周期解：

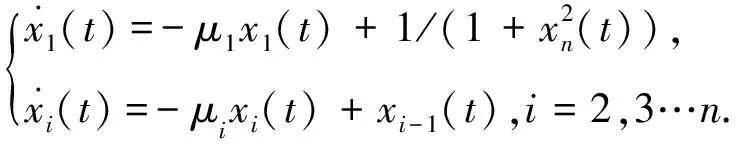
(10)

显然，系统(10)和系统(1)有着相同的平衡点，注意到系统(10)的周期轨道不会穿过x1轴，x2轴，…，xn轴，因此，没有解会穿过坐标轴.另一方面，假设系统(1)有周期解，非常数周期解一定位于第一象限.在第一象限中，我们知道唯一的正周期解E是全局渐近稳定的.因此，系统(1)没有非常数周期解.

定理1如果条件(H1),(H2)和(H3)都满足，则对于每个τ>τj,j≥1,系统(8)至少有j-1个周期解.

证明由第一部分的讨论可知(E,τj,2π/ω)是一个孤立的中心，则存在>0,δ>0和光滑曲线λ∶(τj-δ,τj+δ)→C，使得对任意τ∈[τj-δ,τj+δ],有

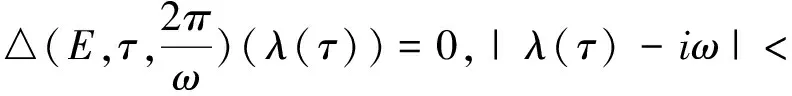
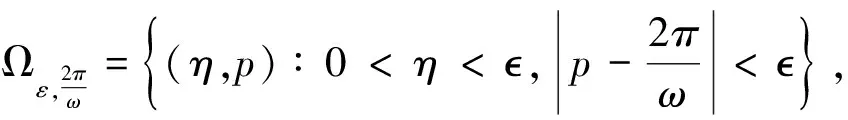
则有横截数

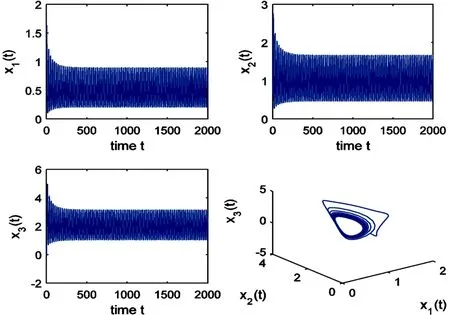
图1 数值模拟图

从(7)式知，当j>0,有2π/ω<τj.由引理7，当τ=0时，系统(8)没有非常数周期解，因此连通分支(E,τj,2π/ω)在τ空间的投影是有下界.如果连通分支(E,τj,2π/ω)在τ空间的投影是有界的，且包含于(0,τ*),τ*>τj.由引理4可知，当时，有p<τ*.意味着连通分支(E,τj,2π/ω)在τ空间的投影是有界的.因此，要使连通分支(E,τj,2π/ω)无界，必须满足连通分支(E,τj,2π/ω)在τ空间的投影无界，即连通分支(E,τj,2π/ω)在τ空间的投影区间包含[τj,∞),因此，当τ>τj,j≥1系统(8)至少有j-1个周期解. 证毕

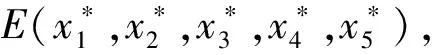
3 小结

本文研究了一类具有多时滞的n维Goodwin模型在正平衡点的稳定性和Hopf分支.当参数τ通过一个临界值时，系统在正平衡点处产生局部Hopf分支,进一步，利用吴建宏等人建立的一般泛函微分方程的全局Hopf分支定理，研究了该模型以时滞τ为参数的全局Hopf分支的存在性，最后给出一个例子结合数值模拟验证了得到的结果.