数学课堂:让思维有迹可循
杨黎琴

摘要:“数学教学要充分暴露思维过程。”只有充分暴露思维过程,才能有效促进思维发展。在小学数学教学中,要让内隐的思维外显(有迹可循),从而提升学生的思维品质,可以从提供实物材料、运用示意图形、借助思维导图三个方面入手。
关键词:小学数学 实物材料 示意图形 思维导图
“数学是思维的科学。”数学思维水平直接影响数学知识的学习和数学问题的解决。离开思维的知识是“死知识”,既无法理解,也不能运用;离开了思维,问题更是无法得到解决。但是,思维是不可见的。因此,“数学教学要充分暴露思维过程”。只有充分暴露思维过程,才能有效促进思维发展。那么,在小学数学教学中,如何才能让内隐的思维外显(有迹可循),从而提升学生的思维品质呢?基于小学生更擅长的形象思维,笔者认为可以从以下几个方面入手。
一、提供实物材料
布鲁纳的认知表征理论指出,“智慧发展的一般进程是,从动作表征经图像表征而达到符号表征的世界”。因此,在小学数学教学中,教师可以提供学生熟悉的、直观化的、可操作的实物材料(学具),通过展示(观察)、演示(操作),让思维有迹可循,为抽象的概念、原理的学习提供形象的支撑。
例如,教学《认识厘米》一课时,教师让学生通过找一找、比一比、画一画、量一量等活动发现身边1厘米的实物材料,然后进行展示,从而充分感知1厘米的表象。学生发现食指的宽、订书钉的宽、卷笔刀的宽、红丝带的宽、小正方体的边长、小方格的边长等是1厘米。在此基础上,让学生通过看一看、说一说、想一想、估一估等活动建构1厘米的概念,进而学会规范地用直尺来画几厘米的线段。这些鲜活的实物材料以及真实的感知活动,使得学生的思维清晰可见,而且提高了思维的发散性。
再如,教学《分数与除法的关系》一课时,在学生理解了“1张饼的几分之几就是几分之几张饼”的基础上,教师提出问题:“3张饼平均分给4个人,每个人分得多少张饼?”同时,提供实物学具,让学生操作演示,从而直观地得出两种分法(见图1),获得“3张饼的14就是34张”的理解。然后,教师追问:“4张饼平均分给5个人,每个人分得多少张饼?”继续让学生操作演示,从而引导学生一步步地建构分数与除法的关系。随着实物学具的操作演示,学生的思维得以外显,思维的灵活性得到提升。
二、运用示意图形
在数学教学中,不是所有的内容都适合或需要实物展示、演示的。很多时候,教师可以引导学生利用比较简洁的实物图或更加抽象的几何图示意,即把实物画下来或把数量转化成图形,进行图像表征。这样,不仅有利于让学生内隐的思维外显,而且有利于学生进一步形成符号表征——尤其在解题教学中,非常有助于学生理解题意,提炼有用的数量关系。
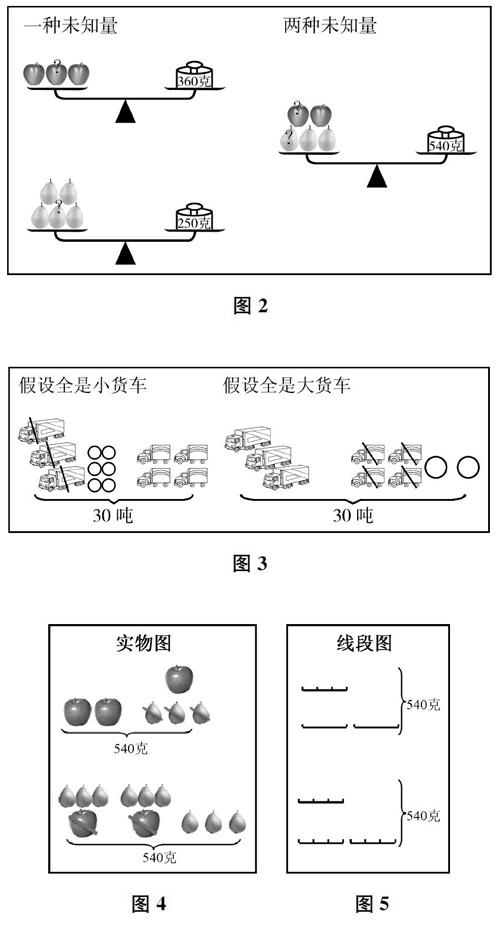
例如,教学《解决问题的策略——假设》一课,教师利用天平称重示意图(见图2),帮助学生直观理解:已知多个一种未知量的和时,可以利用除法求出该未知量;已知多个两种未知量的和时,求不出这两种未知量。从而激发学生探究:怎样才能求出这两种未知量?进而启发学生想到:需要知道这两种未知量之间的关系。接着,教师出示苏教版教材练习十一第2题:“3辆大货车和4辆小货车共运货30吨,大货车的载重量是小货车的2倍,两种货车的载重量各是多少吨?”学生顺理成章地画出货车运货示意图(见图3),得到了解决问题的策略:根据1辆大货车的载重量等于2辆小货车的载重量,假设都是大货车或都是小货车来运30吨货。之后,教师给出图3中后一种情形下两种未知量之间的关系:“1苹果=3梨”。学生解决问题时,不仅画出了实物图(见图4),而且进一步抽象画出了线段图(见图5)。由此,学生暴露出思维过程,得到了可以求解的数量关系(符号表征)。
三、借助思维导图
相对而言,认知表征方式的三种方式,更多地局限于呈现静态、孤立的思维结果。要更好地呈现动态、联系的思维过程和知识体系,从而真正激活思维应用,打通认知结构,就需要借助思维导图。思维导图是思维可视化的重要工具,它与大脑处理事物的自然方式相一致。它最重要的特征不是“图”——实际上它是图文并茂的,而是“导”——呈现出动态的过程和相互的联系,故可以分为“流程导图”和“关系导图”两类。它不仅可以促进学生的思维发展,而且可以提升学生的知识记忆。
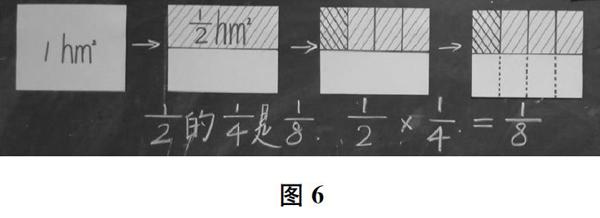
例如,教学《分数乘法》新授课时,教师出示问题:“李大伯家有一块1/2公顷的菜地,其中1/4用来種土豆,3/4用来种玉米,用来种土豆的菜地有多少公顷?用来种玉米的菜地有多少公顷?”学生尝试解答后,教师引导学生利用如图6所示的“流程导图”把快速滑过的思维过程像“慢镜头”一样呈现出来,从而帮助学生理解分数乘法的意义,挖掘分数乘法的算理,并且提高思维的严密性。
再如,教学《分数乘法》单元的复习课时,教师从算法、算理、应用等方面入手,利用如图7所示的“关系导图”帮助学生掌握知识点之间的联系与区别,回顾学习时的思维过程,总结本单元的知识体系。然后,又引导学生针对其中的一些知识点进一步绘制更翔实的“关系导图”,让学生的思维有迹可循,思维的灵活性得到提升,所学的知识更加系统化。图8便是学生绘制的一个“关系导图”。
参考文献:
[1] 单尊.数学是思维的科学[J].数学通报,2001(6).
[2] 张乃达.充分暴露数学思维过程是数学教学的指导原则[J].数学通报,1987(3).
[3] M.P.德里斯科尔.学习心理学——面向教学的取向(第三版)[M].王小明,等译.上海:华东师范大学出版社,2008.
[4] 约翰·哈蒂.可见的学习(教师版)[M].金莺莲,洪超,裴新宁,译.北京:教育科学出版社,2015.
[5] 陈花.“感受数形结合思想的内在力量”的实践与思考[J].教育界,2015(34).

