深度学习，从学生的提问开始

赵劲松

摘要：《圆的周长》一课教学的框架是让学生经历一个由猜测到验证的“再发现”过程。但是，要注意过于顺畅的环节推进是否遮掩了学生可能萌生的问题，让其涌动的思维成为静默的暗流。深度学习，理应从学生的提问开始。本节课的教学可以分为五个环节：对课题提问，确定方向，初步解决;对数据提问，直面困惑，大胆推测;对方法提问，基于困惑，走进历史;对结论提问，质疑批判，追根寻底;对全课提问，回顾总结，存疑拓展。

关键词：深度学习 学生提问 圆周率 《圆的周长》

听过几节《圆的周长》的课，教学框架基本相同：先出示两（几）个圆，请学生比较哪个圆的周长长一些，思考周长与什么有关，猜测周长是直径的几倍;进而引导学生通过实验验证，发现周长总是直径的三倍多一点;在此基础上给出定论，介绍圆周率及其历史;最后，引导学生推导圆的周长公式并运用。

这个框架总体上没有问题，让学生经历了一个由猜测到验证的“再发现”过程。然而，过于顺畅的环节推进是否遮掩了学生可能萌生的问题，让其涌动的思维成为静默的暗流呢？比如：猜测周长是直径的几倍时，学生考虑的是特殊的、具体的圆，还是普遍的、抽象的圆？用“误差”就可以消除学生对“倍数不相等”的疑惑了吗？对于作为文化点缀的“割圆术”，学生的理解又是怎样的“自以为然”？学生对“圆周率是一个无限不循环小数”有怀疑吗？……

有人说，改变世界的不是答案，而是问题。我深以为然。深度学习，理应从学生的提问开始。

一、教學实践

（一）对课题提问，确定方向，初步解决

师（板书课题：圆的周长）看到这个课题，你想到了哪些问题？

生圆的周长怎么算？

生圆的周长怎么量？

生圆的周长与直径、半径有什么关系？

师（逐一板书学生的问题）下面我们就来研究这些问题。把你已经有的想法在小组里说一说，同时听一听同伴的思考。

（学生小组交流。）

师请各小组汇报能够解决的问题。

生用一根绳子围着圆绕一周，再拉直，就可以量出圆的周长。

生还可以把圆放在尺子上滚一周，看滚了多远，就是圆的周长。

师（分别用课件演示两种方法）其实刚才两种方法都做了一件事情，把围成圆的曲线——

生拉直了。

师好，我们解决了怎么量的问题。还能解决什么问题？

生我们认为，圆的半径或直径越长，它的周长就越长。

师你们发现了周长和直径、半径有关系，具体是什么关系呢？

生我觉得，圆的周长比两条直径要长。上半部分是一条曲线，比直径长;下半部分也是一条曲线，也比直径长。

师真好，有理有据！比两条直径长，换句话说就是——

生圆的周长比直径的两倍要多。

师（出示一个直径5厘米的圆）你认为这个圆的周长是直径的几倍？

生2倍多，大约2.5倍。

师（出示一个直径40厘米的圆）这个圆呢？

生也是2.5倍。

师有不同想法吗？

生我认为，两个圆的周长都是直径的3倍。

生我认为，两个圆的周长都是直径的5倍。

生我认为，应该都是3倍多一点。

师尽管刚才几位同学猜测的倍数不同，但是他们的猜测有一个共同的地方——

生两个的倍数关系是一样的。

师有不同想法吗？

生我想说，你们的眼力怎么可能这么好，一眼就看出来是几倍。我认为，倍数关系不可能完全一样。

生一个圆的周长变大，直径也会变大，所以我认为，倍数是一样的。

师听明白了，你们认为倍数相同，靠的不仅仅是眼睛的观察，还有大脑的分析。两位同学都很棒，请坚持自己的观点。假如这个倍数是固定的，黑板上有一个问题就可以解决了——

生用直径乘倍数就可以算出周长。

师如果是不一样的，还能这样计算吗？

生不能。

师看来，这个倍数是不是固定的，很值得研究。怎么研究呢？

生量出几个圆的周长和直径，计算倍数，比一比，看看到底一样不一样。

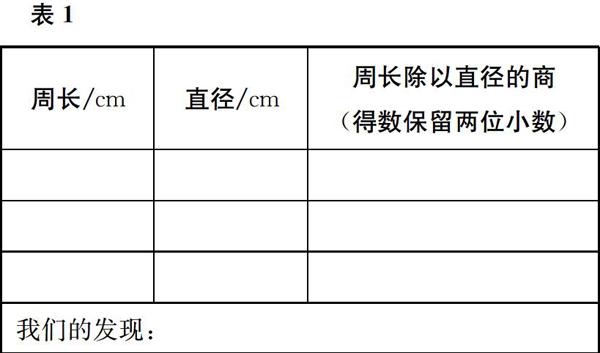
（学生分组实验，填写表1。其中，两个小组的圆相同，由教师提供;其他小组的圆自备。）

（二）对数据提问，直面困惑，大胆推测

生（一个小组汇报）……我们发现，倍数是不固定的。

师各小组的实验结果都是这样的吗？有什么问题吗？

生按理说应该是一样的啊，为什么结果却是不一样的？

生我知道这个倍数是3.14，但为什么我们通过做实验得不到？

师是我们前面的“感觉”出问题了吗？

生不是。尽管我们测量得到的倍数不一样，但这是因为我们没有专业的测量工具，所以测量是有误差的。

生你怎么知道我们的测量有误差呢？

生只要测量就会有误差。

（两位学生争执不下。）

师（出示持相同学具的两个小组填写的表格）两个小组测量同样的圆，结果却不一样，意味着什么？

生意味着有误差。

师（出示持不同学具的两个小组填写的表格）尽管有误差，但我们发现，这两个大小差距这么大的圆，倍数却也差不多。这又意味着什么呢？

生说明这个倍数可能是固定的。

生我不同意。有误差，所以倍数不一样，但也不能说明，没有误差，就一定一样。你们只是在推测，我还是感觉倍数不完全一样，除非你们用“真理”来推翻我。

生我国古代的数学家早就算出来这个倍数在3.1415926到3.1415927之间。

师“真理”来了，你服气吗？

生不服气，这个数是怎么得来的啊？

（三）对方法提问，基于困惑，走进历史

师我们的祖先在很早的时候就发现，圆的周长与直径有关。就和同学们一样，通过测量得出了一个大约的结论：周三径一。1700多年前，我国数学家刘徽发明了一种新的研究圆的周长的方法——割圆术。你有什么想问的吗？

生割圆术是把圆分割成很多个扇形吗？

生割完了要不要量？

师（课件演示将圆周平均分割成六份，连接六个点形成正六边形）这个正六边形很特殊，你看出它特殊在哪里了吗？

生正六边形的边长和圆的半径相等。

生正六边形的周长是圆的直径的3倍。

师正六边形的周长和圆的周长比較呢？

生圆的周长比正六边形的长，所以应该是直径的3倍多。

师（课件演示将圆周继续分割，得到正十二边形、正二十四边形……）正多边形的周长越来越怎么样？

生接近圆的周长。

师刘徽正是用这种方法一直分割到正192边形，求得了3.14这个数值。

生刘徽怎么能把图形画得那么标准呢？

生到了正192边形的时候，圆周上能点下那么多点吗？

师同学们问得很好！确实很难画出。假设真的画出了正192边形，你认为接下来会怎么做？会用尺子来测量一条边的长度再乘192吗？

生不会，太麻烦了。

师仅仅是麻烦吗？

生还因为只要测量，就会有误差。

师所以，这样看来，你们认为刘徽真的把正192边形画出来了吗？

生可能没有吧。但又是怎么得到3.14的呢？

师割圆术之所以能得到更精确的结果，是因为方法的改变。它是一种根据半径来计算多边形边长的方法。具体如何算，你们要到中学才能理解。割圆术让我们确定了圆的周长相对于直径的倍数是一个固定的数，我们把这个数叫作——

生圆周率。

（四）对结论提问，质疑批判，追根寻底

师又过了大约200年，数学家祖冲之进一步发展了割圆术，分割到了正24576边形，把圆周率算到了小数点后七位，领先世界1000多年。当然，国外的数学家在这方面的研究成果同样非常伟大，他们又发明了新的研究方法。到了近代，圆周率已经算到了小数点后面很多很多位。（出示下页图1）你看到了什么？

生看到没有规律的无限小数。

生就是无限不循环小数。

师他们看到了无限不循环小数。有向他们提问的吗？

生如果继续往后算，可能会到头吧？会算到有限的吧？

生到后面可能会循环吧？因为省略号后面是未知的。

师我喜欢你们提出的问题！你们现在还坚信它是一个无限不循环小数吗？

生不确定了。

师但是，现代的计算机已经算到了小数点后数十万亿位，都没发现循环。

生不管算到多少，后面只要还有，就有可能循环。

师我欣赏你的坚持！就像这样算下去，能让我们安心地认为它就是一个无限不循环小数吗？

生永远都不能。

师是的，除非用另一种方法来证明。200多年前，德国数学家兰伯特就用数学的方法证明了它是一个无限不循环小数。对此，大家到高中会再接触。

（教师引导学生归纳公式，解决问题。）

（五）对全课提问，回顾总结，存疑拓展

师今天我们研究的主角是——

生圆周率。

师关于它，你了解了什么？

生是周长相对于直径的倍数。

生是一个固定的数。

生是一个无限不循环小数。

生用π表示。

生一般取近似值3.14。

师从“3”到“3.14”，再到“3.1415926”，最后到无穷无尽，在逐步走向精确、走向完美的过程中，又蕴含了多少古今数学家毕生的心血啊！在这节课中，老师特别欣赏你们的敢于提问、敢于质疑，特别佩服那位让大家用“真理”来说服她的同学！学到这儿，对于圆的周长，你还有什么问题呢？

生一个圆的周长到底能不能准确地得到？

生圆周率为什么一般取值3.14？能不能往后多保留几位小数？

生为什么用“π”来表示圆周率？

师带着问题，我们可以课后继续研究。

二、教学反思

提出一个问题比解决一个问题更重要。因为我们知道，提出问题是对新知的渴求与探索，是对已知的质疑与批判，往往意味着创造的开始。然而，事实上，我们却很少让学生自己提出问题，更多的是让他们解决我们提出的问题。这背后，是立场的问题：教学应该站在知识的立场，还是站在学生的立场？

圆周率是本课的中心内容。作为一个内涵无比丰富的概念，如何切入？如何研究？如何确认？这是一个由模糊到清晰的过程。在这个过程中，学生的思维会有怎样的“暗流涌动”？得让学生提出自己的问题。

实验一直被看作认识圆周率的关键一环。可是，学生能通过实验得到圆周率吗？显然不能。学生在实验前通过观察、推理，猜测周长与直径的商是一个固定值，而实验最终得到的比值必将不是一个固定值，教材的目标定位也只是让学生发现“三倍多一点”。若就此给出定论，学生会服气吗？课堂上，我印象最深的是一个女生。在圆的周长除以直径的商是不是一个固定值的判断上，她几乎是孤身一人对抗整个班级。随后的实验数据支持了她的观点，却被“误差”的说法推翻，但她坚持自己的怀疑态度：“有误差，所以倍数不一样，但也不能说明，没有误差，就一定一样……除非你们用‘真理来推翻我。”我感动于她的坚持。这是对实验方法的质疑、对所得结论的质疑，也是对“真理”的渴盼。教学中，我以两组相同的学具得出的不同数据让学生看到误差的存在，再以两个大小悬殊的圆所得的倍数相差不多让学生感到倍数可能是一个固定的数。可喜的是，她依然不买账，因为这还不是“真理”。学生思维的暗流正是通过提问得以搅动、汹涌，更精确的研究方法的出场也才成为迫切的需求。

圆周率的研究历史不能只是文化点缀般的介绍。仅仅抛给学生一个“割圆术”的名称、一个“无限接近圆”的遐想、一个“领先世界1000多年”的骄傲，都不能击中学生的“痛点”，都不是学生想要的“真理”。割圆术的意义在于方法的革新。课堂上，学生不仅仅是听众，更是思维的参与者、问题的发现者、“历史”的推动者。“是把圆分割成很多个扇形吗？”“割完了要不要量？”“怎么能把图形画得那么标准呢？”“圆周上能点下那么多点吗？”“又是怎么得到3.14的呢？”这些问题的提出彰显着学生的好奇，也暴露出他们的错误理解。学生当然看不懂割圆术的算法，但是，最起码得让他们知道是怎样割圆的，特别是割圆之后不是通过测量而是通过计算得出结果的，正是因为方法的本质改变，所以才能得出固定的、精确的数值。

圆周率是一个无限不循环小数。想象一下，无穷无尽，永不重复，永远不会被定论，永远值得探索。对于学生来说，一定是十分神奇的。然而，教学中仅仅是让学生发出一声惊叹吗？惊叹的背后难道就是轻信、盲从，而没有一丝疑惑吗？这是学生认识的第一个“纯天然”的无理数。既然是无限不循环的，那我们是怎么知道它是无限的，又是怎么确定它是不循环的呢？很高兴，课堂上学生发出了这样的声音。

五次让学生提问，从课始的“是什么”“怎么做”这类最基础的未知问题，明确方向，展开研究，到学习过程中对方法、结论的科学性大胆质疑，敢于怀疑“是真的吗”，敢于追问“为什么”，再到课尾提出新的问题，萌发新的思考，逐渐让思维向深处漫溯，让深度学习发生。

提出问题当然意味着可以更好地解决问题，但其本身就是主动学习的开始，是高阶思维的体现，是值得我们去研究的更重要的事情。

*本文系安徽省教育科学研究项目“核心素养视域下小学数学基于‘真问题教学的实践研究”（编号：JK19103）的阶段性研究成果。

参考文献：

[1] 孙四周.还原祖冲之——我是如何在中学讲割圆术的[J].教育研究与评论，2016（6）.

[2] 张景中.从2谈起（典藏版）[M].北京：中国少年儿童出版社，2011.