行列式在立体几何中的应用

范峻培

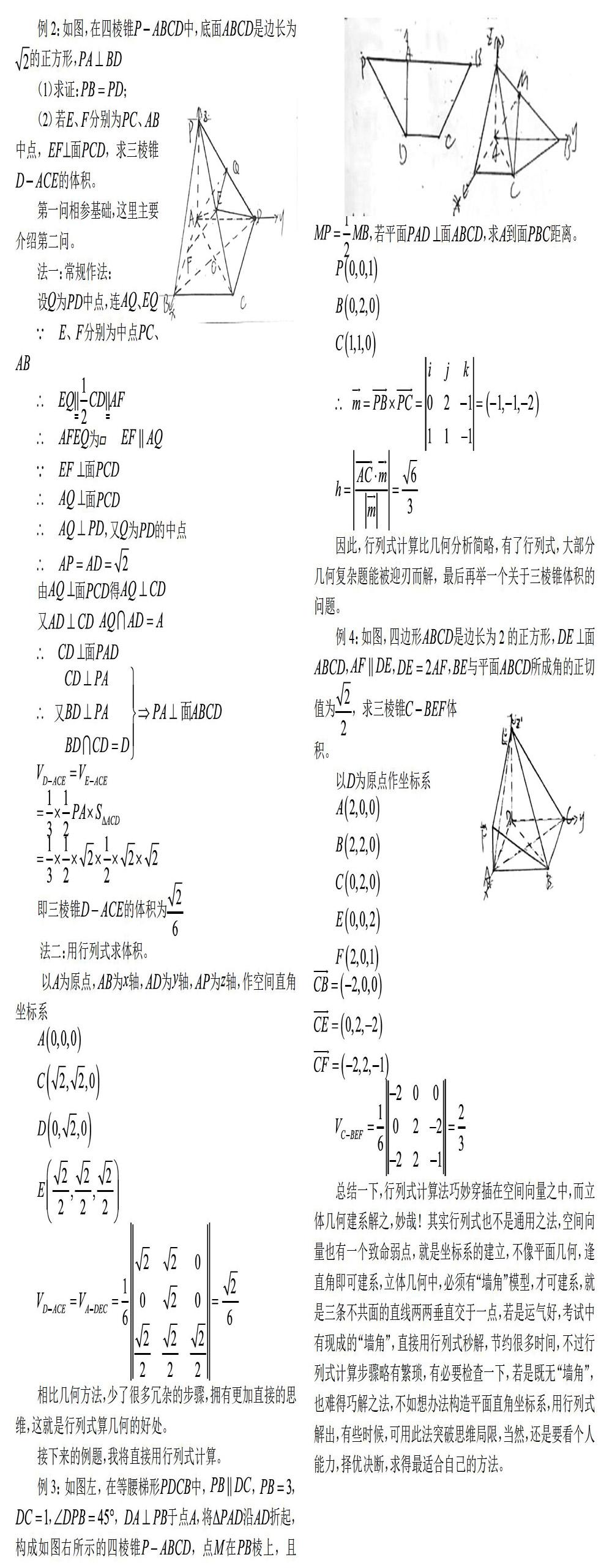
摘 要 行列式可以看做是有向面积或体积的概念在一般的欧几里得空间中的推广，在高考的几何问题中能得到很好的应用。本论文简要介绍了二阶、三阶行列式形式，并从平面法向量、空间三角锥体积两方面介绍了三阶行列式的具体用法。

关键词 行列式 法向量 空间三棱锥体积

中图分类号：G632文献标识码：A

同样，运用行列式，更加简单粗暴地算出点面距离，其优势在于非常的直观，一目之了然。

可能有人会认为，直接用几何方法做，也不会难到哪去，事实上，是由于将点面距离转换求解可能相对简单，因此，下面我将引入另一个令人头疼的问题，体积问题，求三棱锥的体积相比点面距离就复杂一些，本质是一样的，但有时需利用体积转换，不然难以求得点面距离。

总结一下，行列式计算法巧妙穿插在空间向量之中，而立体几何建系解之，妙哉！其实行列式也不是通用之法，空间向量也有一個致命弱点，就是坐标系的建立，不像平面几何，逢直角即可建系，立体几何中，必须有“墙角”模型，才可建系，就是三条不共面的直线两两垂直交于一点，若是运气好，考试中有现成的“墙角”，直接用行列式秒解，节约很多时间，不过行列式计算步骤略有繁琐，有必要检查一下，若是既无“墙角”，也难得巧解之法，不如想办法构造平面直角坐标系，用行列式解出，有些时候，可用此法突破思维局限，当然，还是要看个人能力，择优决断，求得最适合自己的方法。