在“猜想、证明与拓广”中积累数学基本活动经验

刘莹

【摘要】数学的知识、思想、方法、技能只有经过一定的数学基本活动经验的积累才能内化为学生的数学素养.综合与实践活动为数学基本活动经验的积累提供了平台，本文对“猜想、证明与拓广”教学中学生数学基本活动经验的积累进行了分析.

【关键词】综合与实践;数学基本活动经验;猜想;证明;拓广

数学基本活动经验作为课程目标之一在《义务教育数学课程标准（2011年版）》中被明确提出，可以理解为学生从经历的数学活动过程中获得的感受、体验、领悟以及数学知识、技能、情感与观念等内容组成的有机组合性经验[1].综合实践活动的形式多种多样，包括观察、猜想、验证、推理与交流等数学活动，学生要综合自己的知识，运用数学的思维模式进行课题的研究，因此，综合实践活动是积累数学基本活动经验的重要载体.“猜想、证明与拓广”（第一课时）选自北师大版课标教材九年级上册综合与实践，主要探究矩形的“倍增”与“减半”问题.本文分析了这节综合与实践课对学生积累数学基本活动经验的独特价值.

一、课堂教学实录

（一）探究活动1：正方形的“倍增”问题

1.猜想环节

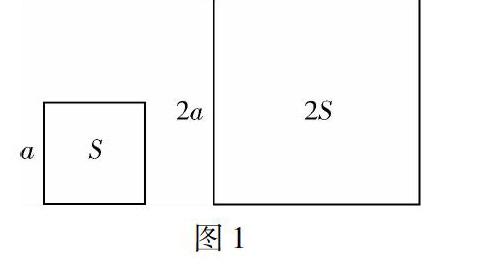
师：任意给定一个正方形，是否存在另一个正方形，它的周长与面积分别是已知正方形周长和面积的2倍？大家大胆猜想一下.

（教师板书并画图（如图1所示），学生交流讨论）

生：不存在.

师：是怎么考虑的？

生：特殊值验算，设原正方形边长为2，所要求的正方形的周长应该为16，那么它的边长为4，面积为16，不是原来的2倍.

（教师板书猜想）

2.证明环节

师：仅凭这样一个例子可以直接判定不存在吗，还是不一定存在呢？

生：不能判定，这只是一个特殊情况，只能作为一种猜想的依据.

师：怎么给出一般性的证明呢？

生：用字母表示边长.

师：好，那我们任意给定一个正方形，设它的边长为a，则周长为4a，面積为a2.那么该如何证明呢？

（小组内交流讨论，小组代表发言）

生：如果存在满足条件的正方形，假如周长是原来的2倍，那么它的边长应该为2a，但是此时面积为4a2，不是原来的2倍，因此，不存在满足条件的正方形.

生：假如所求正方形的面积满足是原来的2倍，它的边长应该为2a，那么此时正方形的周长是42a，变成了原来的2倍，因此，不存在满足条件的正方形.

师：很好，你们都是从代数角度考虑的，从正方形的几何特性考虑一下，还有别的方法吗？

生：利用相似来做，如果存在，这两个正方形一定相似，所以可设相似比为k，则周长比为k，面积比为k2，由题意可得k=k2=2，这样的k不存在，故这样的正方形不存在.

师：非常好，同学们用三种方法证明了猜想.我们来总结一下：方法一，固定周长，看面积是否满足条件;方法二，固定面积，看周长是否符合条件;方法三，利用相似图形的性质证明.谁来表述一下结论？

生：任意给定一个正方形，不存在另一个正方形，它的周长与面积分别是已知正方形周长和面积的2倍.

3.拓广环节

师：刚才我们研究的是正方形的“倍增”问题，其他的图形有这样的性质吗？你们能拓广一下吗？

生：将正方形改为矩形.

师：用语言表述一下.

生：（猜想一）任意给定一个矩形，是否存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的2倍？

生：（猜想二）任意给定一个三角形，是否存在另一个三角形，它的周长和面积分别是已知三角形周长和面积的2倍？

师：好，同学们不拘泥于四边形，将边数扩展到三条边了.

生：（猜想三）任意给定一个圆，是否存在另一个圆，它的周长和面积分别是已知圆周长和面积的2倍？

师：好，现在又拓广到圆了.

师：那么对于这些猜想，同学们最想探究哪一个呢？

生：矩形，正方形是特殊的矩形，我们证明了正方形的结论，它的进一步拓广就是矩形，就探究一下矩形吧.

师：大家同意吗？

生：同意！

（二）探究活动2：矩形的“倍增”问题

1.猜想环节

师：那我们接下来一起猜想一下有关矩形的这个结论，存在这样的矩形吗？大家想怎么探究呢？小组交流一下.

生：可以确定的是，不存在满足要求并且与已知矩形相似的矩形.

生：探究正方形的方法也是适用的.可以先找个特殊的矩形验证一下，再进行猜想.

生：直接用字母表示之后得出一般性结论.

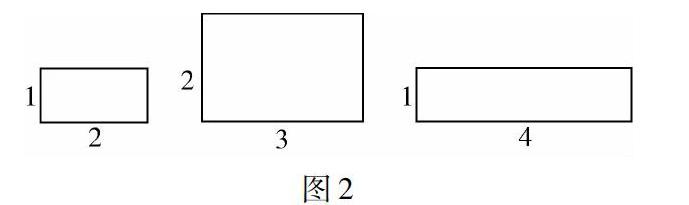
师：同学们的想法都很好，直接用字母表示来验证是可行的，我们验证几个特例可以理清计算的思路，减少后续计算的困难.大家计算一下以下几个矩形（如图2所示）并验证结论.

（以学习小组为单位进行探究活动，每个小组选择一种情况进行验证，整理并写出完整的解答过程，尝试多种方法解决）

师：同学们说一下第一个长为2、宽为1的矩形，大家找到满足条件的矩形了吗？怎么做的呢？

生：先固定所求矩形的周长，周长为12，设所求矩形的长为x，那么它的宽为6-x，而它的面积为x（6-x），满足的关系式为x（6-x）=4.转化为一元二次方程x2-6x+4=0，计算可得所求的矩形长为3+5，宽为3-5.

生：先固定所求矩形的面积，面积为4，设所求矩形的长为x，那么它的宽为4x，而它的周长为2x+4x，满足的关系式为2x+4x=12.转化为分式方程x+4x=6，计算可得所求的矩形长为3+5，宽为3-5.

生：设所求矩形的长为x，宽为y，那么满足方程组x+y=6，xy=4， 对这个方程我们在解的程中遇到了一些困难.

师：好，同学们如何解这个方程组呢？大家一块讨论一下.

（小组交流讨论，小组代表发言）

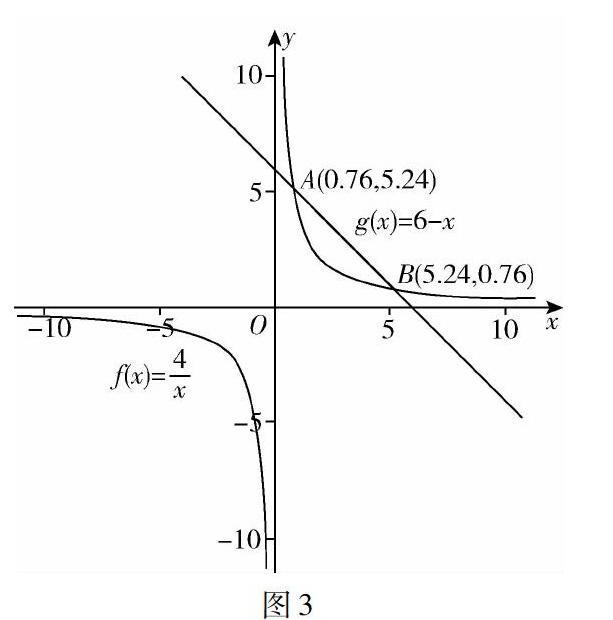
生：xy=4将x除过去可以转化为反比例函数y=4x，这是我们所熟悉的.将x+y=6变形可得y=6-x，方程组的解可以看作这两个函数图像的交点.

师：好，同学们用GeoGebra软件操作一下，将它的求解出来.

生：由函数图像（图3）可得方程组有解，因此，存在这样的矩形.

师：同学们将图形的问题转化为方程问题，方程的解又可以借助函数图像来解决，真正地做到了数形结合.经过刚才的交流，大家解决问题的方法是不是又丰富了呢？再给大家一些时间，解决剩下的两个问题，小组交流讨论.

师：现在给出你们的猜想吧.

生：任意给定一个矩形，存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的2倍.

2.证明环节

师：大家通过几个特例给出了猜想，下面我们来探究一下一般的情况.

生：假设已知矩形的长和宽分别为a和b，那么已知矩形的周长和面积分别为2（a+b）和ab，先固定所求矩形的周长，周长为4（a+b），设所求矩形的长为x，那么它的宽为2（a+b）-x，而它的面积为x[2（a+b）-x]，满足的关系式为x[2（a+b）-x]=2ab.将关系式变形得到一元二次方程x2-2（a+b）x+2ab=0，判别式Δ=4（a2+b2）显然是大于0的，说明方程有解，因此，所要求的矩形是存在的.

师：其他小组还有不一样的做法吗？

生：还可以先固定面积，所求矩形的面积为2ab，设所求矩形的长为x，那么它的宽为2abx，而它的周长为2x+2abx，满足的关系式为2x+2abx=4（a+b）.这是一个分式方程，经过变形整理，可以得到方程x2-2（a+b）x+2ab=0，同样Δ=4（a2+b2）>0，可以得到方程有解.

师：大家都是转化为一元二次方程来求解的，但是只用Δ=4（a2+b2）>0来判断可以吗？是不是忽略了什么条件？

（众生沉默）

师：大家想一下对一个一元二次方程来说Δ>0能说明什么呢？

生：说明方程两个不相等的实数根.

生：矩形的边长显然是大于零的，因此，只说明方程有两个不相等的实数根是不行的，还得说明有大于0的实根.

生：对，这里的x是大于0的，我们都忽略了.

师：同学们，这个经验告诉我们数学是严谨的，我們在给出任何一个变量时都要明确它的范围，容不得半点马虎，不然就会出现严重的错误，接下来请大家思考如何来说明方程有大于0的实根.

（小组交流讨论）

师：大家有思路了吗？

师：看来带有字母的方程对大家来说还是有些困难的.我提示一下，给定的x是大于0的，给定的a，b也是大于0的.大家再讨论一下.

（学生获得提示后，积极思考，讨论气氛热烈）

生：韦达定理可以说明.根据Δ>0我们可以知道方程有两个实数根，那么假设方程的两个实数根为x1和x2，则x1+x2=2（a+b），x1x2=2ab， a+b>0，ab>0，两根之积要大于0，则两个根同号，两根之和又要大于0，则只能x1，x2都是大于0的.因此，也能说明方程是有大于0的实数根的.

师：非常正确.善于思考就能面对大的挑战.

师：根据我们求解特例的经验应该还有其他的做法，大家能够想出来吗？

生：我们小组是这样解的.设所求矩形的长和宽分别为x和y，这里x和y就是大于0的.列出方程组x+y=2（a+b），xy=ab， 这个方程组的解可以看作函数y=-x+2（a+b）和函数y=abx的交点，并且交点要满足x>0，y>0，x≥y， 只是不会用软件画图.

师：分析得非常正确，并且考虑了未知数的范围.我们接下来共同学习用GeoGebra动态演示带有变量的函数的画法.

（教师用软件演示（如图4所示），并请学生进行动态演示）

生：可以看出有满足条件的交点，所以这样的矩形是存在的.

师：这样就验证了我们的猜想.请同学们来表述结论.

生：任意给定一个矩形，一定存在另一个矩形，它的周长和面积分别是已知矩形周长和面积的两倍.

3.拓广环节

师：同学们，本节课研究了正方形与矩形的“倍增”问题，同学们已经在图形上进行了拓广，想一想还能从哪些方面进行拓广呢？

生：将2倍改成3倍、4倍或者改为一半.

师：类比本节课的探究方法，我们将矩形的“减半”问题留为作业，小组探究解决，并且将结论写成小论文的形式，下节课我们进行汇报展示.

二、综合与实践活动——数学基本活动经验的积累的平台

（一）综合、体验与创新

本课题虽然是“纯数学”的探究活动，但却充分体现了综合与实践活动的“综合性”“体验性”与“创新性”[1].首先既考查了图形相似，又考查了方程的求解以及几何与代数领域知识的综合.既可以先固定周长看面积是否满足2倍关系，也可以先固定面积看周长是否满足2倍关系，用到了物理、生物学科实验经常使用的控制变量法，体现了数学与其他学科知识的综合.在解决问题的过程中GeoGebra软件是师生得出结论的重要工具，体现了数学与信息技术的综合.其次，学生在解决问题的过程中，体验了特例入手、归纳猜想、证明猜想、拓广结论的数学思维的全过程.再次，课题本身就具有开放性与挑战性，所以需要学生对所学知识进行判断、选择和创新性运用，比如，学生运用韦达定理证明方程有大于零的实数根就十分具有创新性.

（二）学生经验的积累

学生在研究正方形的面积时，由特殊值验证过渡到用字母表示数量关系得出一般性的结论，由常量到变量，运用符号进行数学问题的表达，经历运算、推理和数学思考的一系列过程，积累了运用数学符号的经验.通过画图，标注数量关系来描述问题、理解问题，在形象思维的基础上进行推导、验证得到结论，积累了几何直观的经验.在处理方程时，学生通过适当的变形识别出一次函数、反比例函数，使计算更加简便.在一元二次方程是否有实根的判断上，不同的学生采用了不同的方法，如用一元二次方程根的判别式或配方法，积累了简洁运算的经验.学生在学习过程中经历了“理解问题→初步猜想→验证→发现规律→证明→拓广”的数学化的过程，形成了科学探究的一般思维模式，积累了模型经验.学生由正方形的“倍增”问题过渡到矩形的“倍增”问题，由特殊的情形到一般性问题，用合情推理进行猜想，用演绎推理验证猜想，积累了数学推理的经验.小组合作探究，学生之间集思广益，相互启发，辩证思考，客观表达，敢于质疑，善于归纳，积累了数学交流的经验.

综合与实践活动是积累数学基本活动经验的良好载体[2]，教师在教学过程中应该重视综合与实践活动课题的教学，鼓励学生动手实践、自主探索、合作学习，将数学的知识、思想、方法、技能内化为数学素养.

【参考文献】

[1]仲秀英.学生数学活动经验的内涵探究[J].课程·教材·教法，2010（10）：52-56.

[2]傅海伦.数学新课程教学论[M].山东：山东教育出版社，2014.