基于复形法的钢框架结构多目标多层次优化设计

陶清林，徐立洲，孔 炯

(1.安徽工业大学建筑工程学院，安徽马鞍山243032；2.中国十七冶集团有限公司冶金工程技术公司，安徽马鞍山243000)

优化设计是指从所有可行性方案中寻找使目标函数达到预期、效果最满意的方案，工程各环节无不存在优化的问题。结构优化设计思想最早可追溯到1854年Maxwell J C提出的基本原理和1904年Michell A G发展和应用的布局理论(Michell桁架)。1960年，Schmit L A通过用数学规划来解决结构优化设计并取得巨大成功，成为优化方法的理论基础[1]。在过去的几十年中，结构优化理论有了长足的发展，越来越多的设计问题都可以用一系列的运算法则进行优化。Zacharenaki等[2]借助Pushover-IDA工具提出了基于性能的结构设计优化算法，并显著降低了一栋9层钢结构的成本费用；李刚等[3]以构件用量和层间位移角为优化目标，采用多目标遗传算法对分灾结构进行多目标优化设计；徐龙河等[4]以损伤和滞回耗能作为评价指标识别最不利地震动下的失效模式，并用基于性能的多目标优化方法提高结构的抗震性能；李志强等[5]以工程造价最小和斜截面抗剪承载力最大为优化目标，应用最优性准则K-T条件对钢骨混凝土构件的混凝土截面尺寸进行优化设计。但是目前多层次的优化设计在工程结构设计中鲜有报道。

工程结构数学优化有一维探索优化方法、无约束优化方法和约束问题优化方法，其中，约束问题优化方法是工程设计中常见的优化方法，约束问题优化又可分为随机方向法、复合形法、可行方向法、惩罚函数法，前三者属于直接法，惩罚函数法属于间接法[6]。复形法(complex method)作为解决非线性有约束最优规划的可靠方法之一，以其在高灵活性、广搜索域、强不等式约束等方面的绝对优势，受到了工程界的青睐[7]。鉴于此，本文基于钢结构设计理论及复形法优化思想，借助Matlab软件平台运用复形法优化思想分别对钢框架进行结构层次多目标优化分析和构件层次的优化，旨在为结构的优化方法提供思路。

1 复合形法的优化模型

复形法是一种常见的直接搜索法，可用于解决有约束条件的非线性规划问题。复形法基本思想来源于单纯形法，这个方法是在n维受非线性约束的设计空间内，由K ＞(n+1)个顶点构成多面体，成为复形。然后对复形的各顶点函数值逐一进行比较，不断丢掉函数值最劣的顶点，代入满足约束条件，且函数值有所改善的新顶点，如此重复，逐步逼近最优点为止，复形法思维导图如图1。

图1 复形法思维导图Fig.1 The minding map of complex method

复形法由于不必保持规则图形，较之单纯形法更为灵活可变。除此之外，其在探索最优解的过程中，检验整个可行区域，因此所求结果可靠，收敛较快，且能有效地处理不等式约束的问题。和目标函数及约束函数求导数的方法相比，如果函数复杂，或则隐式的话，计算导数较为困难，用复形法有较多的优点[8]。设y=minF(X)，复形法数学模型表达如下：

设计变量

约束条件

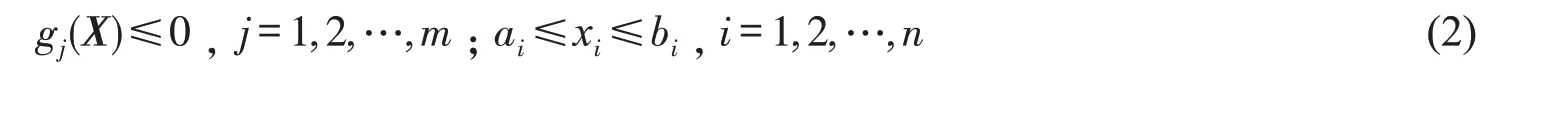
收敛准则

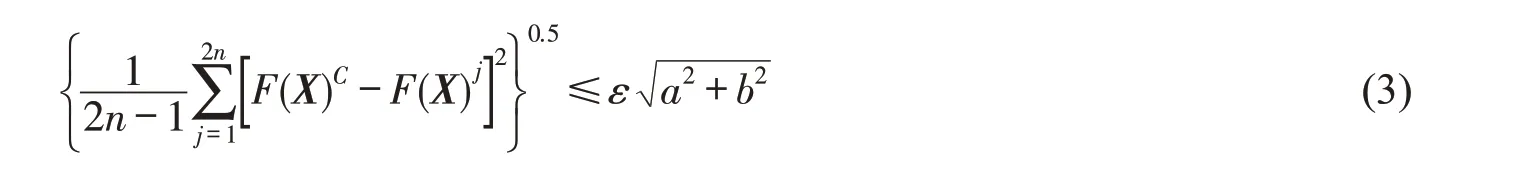
式中：ai和bi为边界条件，表达为设计变量的上限、下限；F(X)C，F(X)j分别为形心处和各顶点处函数值；ε建议取目标函数值的1/1 000 ∼1/100。

2 工程概况

某地一榀两跨六层钢结构框架结构，跨度均为6.3 m，各层层高均为3.3 m，楼板集中质量m1-6=21 000 kg。优化前采用PKPM设计软件中的STS模块进行设计计算，结构计算结果为：风载作用下柱顶最大水平位移，节点(16)dx=16.999 mm=H/1 165 ＜柱顶位移容许值H/500；梁的(恒+活)最大挠跨比1/1 183＜梁的容许挠跨比1/400；梁的(活)最大挠跨比1/3 117＜梁的容许挠跨比1/500；钢柱的总质量3 991 kg；钢梁的总质量4 653 kg；钢梁与钢柱质量8 644 kg。设计所得的梁、柱截面信息如图2，结构参数信息见表1。

图2 PKPM软件设计结果Fig.2 Results of PKPM software design

表1 PKPM软件设计所得结构参数Tab.1 Structural parameters obtained from PKPM software design

3 钢框架结构层次的优化设计

3.1 设计变量

钢框架的梁、柱一般采用宽翼缘组合H 型截面，钢框架结构的内力分布与各杆件的截面惯性矩I、截面积A及截面抵抗拒W有关[8]。工程界常用取值统计结果显示[9]，H 型钢截面面积A及截面抵抗矩W与截面惯性矩I之间有如下关系：，W＝0.78Ix0.75，Iy=0.36Ix。考虑到变量的灵敏度，文中以钢框架梁、柱的惯性矩为设计变量：I=(I1,I2,…,In)T。

3.2 目标函数

以反映抗震性能最优的结构应变能最大化和反映工程造价最低的结构用钢量最小化为优化目标，结构应变能U(I)和工程用钢量V(I)分别按式(4)，(5)计算：

式中：Qnk和δnk分别为第k振型下第n层层间剪力和层间水平位移；N为结构层数；K为振型数；mb为梁个数；mc为柱个数；Ab和Ac分别为梁、柱截面面积，实际工程中常取A=0.80I0.5x。

为保证结构在工程服役期间性能最优的同时减少工程造价，使两者目标方向达到统一，改变应变能项符号，并采用加权系数法将两目标函数转化成一个目标函数，目标函数表达式见式(6)，此时优化目标为使目标函数F(I)达到最小值。

式中：α和β分别为应变能加权系数和工程用钢量加权系数，且α ＞0 ，β ＞0，α+β=1；U0和V0分别为U和V初始值，由起始惯性矩计算得到。

3.3 约束条件

优化过程中，依据钢结构设计标准要求，有钢框架强度、刚度、稳定性等6个约束条件[10]：

1)梁柱强度约束

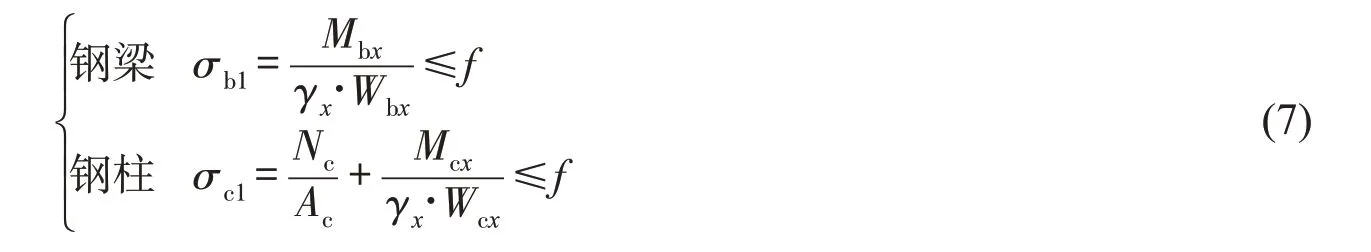
式中：Mbx，Mcx分别为梁、柱截面绕x轴的弯矩设计值；Nc为柱轴向力设计值；γx为截面塑性发展系数(对非直接承受动载构件，常取γx=1.05)；Wbx，Wcx分别为梁、柱截面抵抗矩；Ac为柱截面面积；f为钢材抗拉、抗压和抗弯强度设计值。

2)梁柱刚度约束

3)钢柱稳定约束

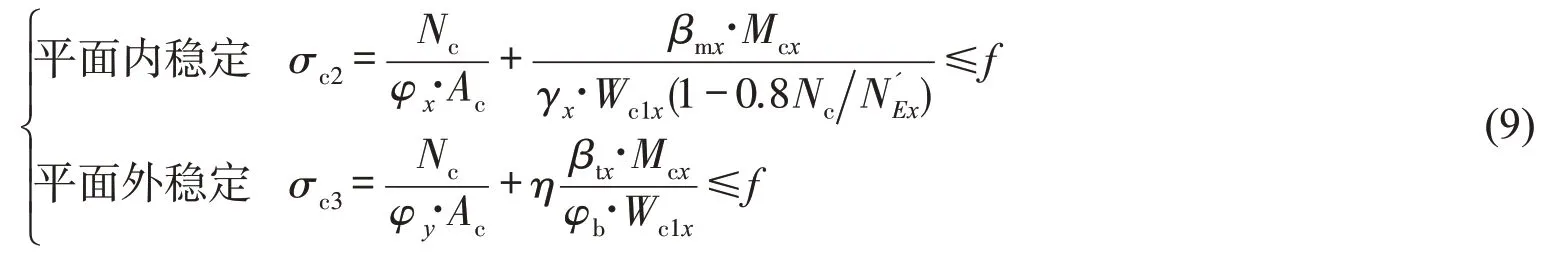
式中：βmx为平面内稳定验算等效弯矩系数，底层柱取1.0，其他层βmx=1-0.36N/Ncr，Ncr为弹性临界力；为参数，；φx，φy分别为弯矩作用平面内和平面外轴心受压构件稳定系数，按规范取值；βtx为平面外稳定验算等效弯矩系数，考虑构件段内有端弯矩和横向荷载同在，使构件段内产生同向曲率时，βtx取1.0；φb为均匀弯矩作用时，构件的整体稳定系数,

4)变形约束

式中柱的抗侧刚度d=12EI h3，对其进行修正，即D=αd=α(12EI h3)。

5)周期约束

为避免产生共振，此结构周期要求控制在不小于0.45 s的范围内，即

式中：ΔT为计算结构基本自振周期用的结构顶点假想侧移；α0为考虑非承重砖墙(填充墙)影响后的基本周期折减系数，框架结构常取α0=0.7 ∼0.8。

6)界限约束

3.4 优化结果分析

依据复形法的操作思想，借助Matlab编程，编写M文件fun1.m和confun.m(约束条件)，在Matlab的命令窗口依次输入。编写条件循环语句，最后使用fmincon优化函数进行校核[11-12]。通过改变目标函数中的加权系数，实现不同加权系数下多目标的优化，所得结果见表2。由表2可看出：当α=0，β=1.0 时，多目标优化变化为用钢量最小的单目标优化，当α=1.0，β=0 时，多目标优化变化为应变能最大的单目标优化；结构的应变能主要由边柱和中柱的惯性矩决定，惯性矩越小，结构的变形能力越大，即结构的应变能越大。

表2 不同加权系数对应结构参数的优化结果Tab.2 Optimization results of the structure corresponding to different weight coefficients

为更好地分析加权系数与优化目标之间的关系，引入初始结构用钢量、结构应变能以消除目标参数在量纲上的不同，得到结构用钢量和结构应变能优化目标与应变能加权系数α之间的关系曲线，结果如图3（图3中优化目标结构用钢量及应变能为量纲为1的量），优化结果显示：结构用钢量和结构应变能优化目标值随着应变能加权系数的增加而增加；优化目标在优化设计函数中的权重由加权系数反映，具体结合结构造价、力学性能等因素的侧重点和导向取值。

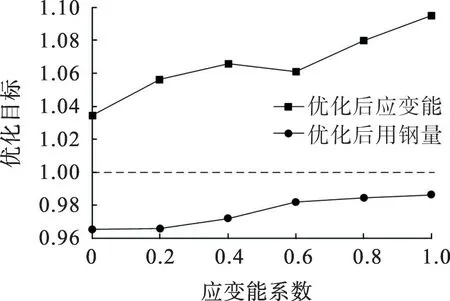
图3 应变能加权系数与优化后结构用钢量应变能的关系Fig.3 Relationship between weighted coefficient of strain energy and dimensionless steel consumption and dimensionless strain energy after optimization

4 钢框架构件层次的优化分析

通过钢框架结构层次优化得到了现行理论设计约束条件下构件的最佳惯性矩，为得到构件的具体参数设计值，在上述结构层次优化结果的基础上，按同样的方法对钢结构构件进行优化。

4.1 数学模型的建立

设计变量

式中各参数物理意义见图4标注。

目标函数

式中W(t)为单位长度下的构件质量。

约束条件

依据前文整体结构优化结果，式中各参数取不同值：依据工程经验，tl=(250,150,5,10)，tu=(800,500,16,30)。

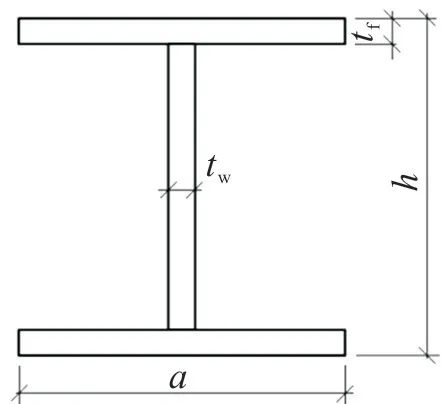
图4 构件截面参数Fig.4 Section parameters of the component

4.2 优化结果分析

Lingo(linear interactive and general optimizer)为交互式的线性和通用优化求解器，以快速精确求解非线性优化问题而被广泛使用，故文中借助Lingo优化软件对钢结构构件进行优化设计。优化后的钢框架梁、柱截面参数列于表5中，值得注意的是表5中的数据完全依据优化所得，若将其应用于实际工程，应适当调整。

表5 基于整体结构优化的构件截面参数优化结果Tab.5 Optimization results of component section based on overall structure optimization

为能直观地观察到加权系数对优化目标的影响，将构件的优化目标值和优化后钢材节约量与加权系数α绘制成图，结果如图5,6。由图5，6可以看出：相对于优化前截面，优化后的钢框架构件截面增加了型钢截面高度，减小了型钢截面宽度；优化过程中，当α≤0.6时，中柱节约量最大、梁次之、边柱最少，当α＞0.6时，中柱节约量最大、边柱次之、梁最少；当加权系数发生变化时，截面高度发生小幅度变化，其余参数无变化，即案例中的截面高度是影响目标函数值的主要因素。

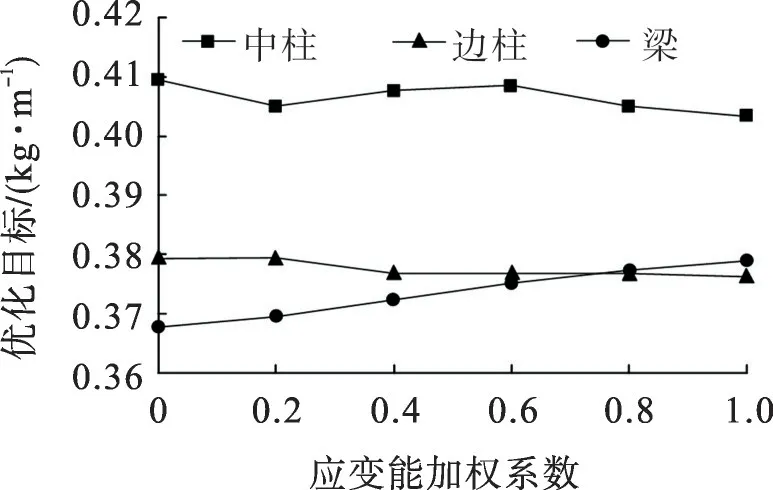
图5 应变能加权系数与目标函数的关系Fig.5 Relationship between weighted coefficient of strain energy and objective function value

图6 应变能加权系数与的单位长度钢材节约比的关系Fig.6 Relationship between weighting coefficient of strain energy and the steel saving ratio

5 结 论

基于复形法思想对钢框架从结构层次和构件层次两方面进行优化，并将优化结果与优化前截面参数进行比较，所得主要结论如下：

1)将钢框架结构的总用钢量和应变能作为优化目标，优化后结构用钢量降低的同时，结构性能也得到了提升，且随着应变能系数的增加，结构总用钢量和结构应变能曲线均呈整体上升趋势；

2)结构应变能主要由边柱和中柱的惯性矩决定，且惯性矩越小，结构变形能力越大，结构应变能也就越大；

3)构件优化过程中，当α≤0.6时，中柱节约量最大、梁次之、边柱最少，当α＞0.6时，中柱节约量最大、边柱次之、梁最少。优化后的钢框架构件截面增加了截面高度，减小了截面宽度，且应变能加权系数发生变化时，截面高度是影响目标函数值的主要因素。