高考复习要注意回归教材

章显联

(浙江省绍兴市鲁迅高级中学 312000)

教材是教师教学 ，学生学习之本，也是高考命题专家命题之源.数学概念，法则，公式的复习不仅要记住结论，更要关注它们的发生，发展过程和本质.下面通过探秘2019年部分高考题的源与流，让我们更懂得需要利用好教材，包括教材中的习题.

一、厉害了，我的角

高考真题【2019年浙江高考8】设三棱锥V-ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点(不含端点)．记直线PB与直线AC所成的角为α，直线PB与平面ABC所成的角为β，二面角P-AC-B的平面角为γ，则( ).

A．β<γ，α<γB．β<α，β<γ

C．β<α，γ<αD．α<β，γ<β

题源揭秘本题的背景是：“最大角与最小角原理”.

探究1已知AP为平面α的斜线，AP与平面α内过P点的所有直线所成的角中，最小的那个角在哪里？

通过直观感知，操作确认，思辨证明得出最小角.

最小角原理：斜线与平面内任何直线所成的角中线面角最小.

三余弦公式：cosγ=cosθ·cos∠CPO.

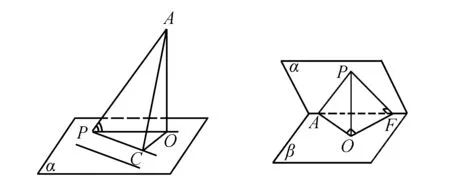
图1 图2

探究2在锐二面角α-l-β中，α内过P点的所有直线中，哪条直线与β所成线面角最大？

通过直观感知，操作确认，思辨证明得出最大角原理及三正弦公式：

最大角原理：在锐二面角α-l-β中，α内的任一直线AP与β所成线面角中二面角的平面角最大.

三正弦公式：sinθ=sinγ·sin∠PAF.

(其中θ为线面角，γ二面角α-l-β的平面角)

真题解答：

法1由最小角原理得β<α，记二面角V-AB-C的平面角为γ′(显然γ=γ′).

由最大角原理得β<γ，故选B.

法2(特殊位置)取V-ABC为正四面体，P是棱VA上的中点，算出α，β，γ的正弦值，可得选项B.

变式问题

变式题1(2018浙江高考8)已知四棱锥S-ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点)，设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S-AB-C的平面角为θ3，则( ).

A．θ1≤θ2≤θ3B．θ3≤θ2≤θ1

C．θ1≤θ3≤θ2D．θ2≤θ3≤θ1

解1作出三个角，通过定量计算得出答案为D.

解2由最小角与最大角原理知：θ1≥θ2,θ3≥θ2，故选D.

变式题2 (2018年11月浙江学考)

四边形ABCD为矩形，沿AC将△ADC翻折成△AD′C.设二面角D′-AB-C的平面角为θ，直线AD′与BC所成的角为θ1，直线AD′与平面ABC所成的角为θ2，当θ为锐角时，有( ).

A．θ2≤θ1≤θB．θ2≤θ≤θ1

C．θ1≤θ2≤θD．θ≤θ2≤θ1

解由最小角原理得θ1≥θ2，由最大角原理得θ≥θ2.下面比较θ1与θ的大小既可.选B.

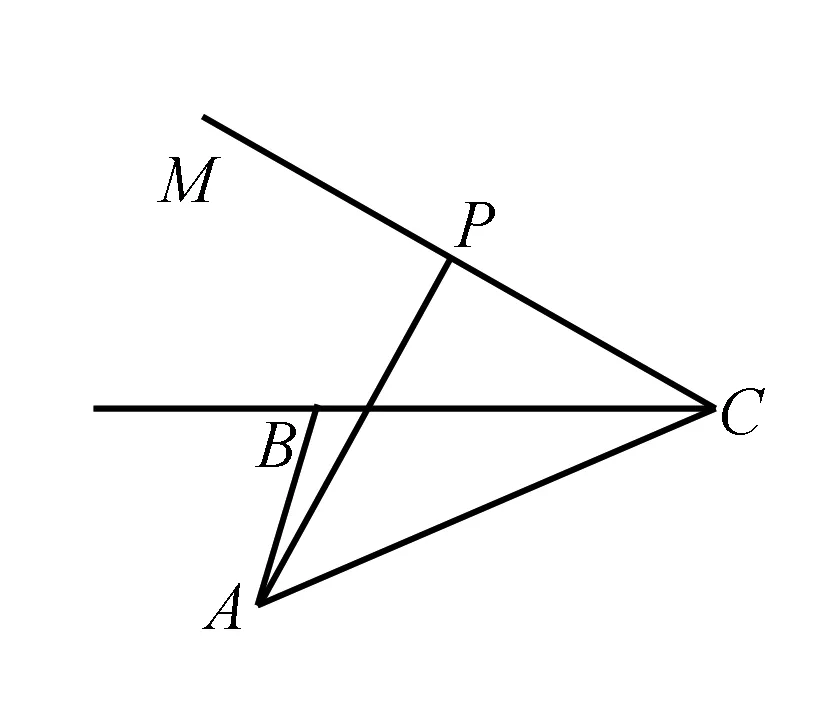
图3

变式题3(2014年浙江高考17)如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面的射击线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值为____.

解1函数思想

∵AB=15,AC=25,∴BC=20.设P点到地面垂足为N，h=PN,则

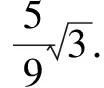
解2由线面角≤面面角，求tanθ的最大值转化为求二面角M-AC-Q的平面角.

变式题4若异面直线a,b所成的角为50°，P为空间一定点，则过点P与a,b所成角都是30°的直线有( ).

A．一条 B.二条 C.三条 D四条

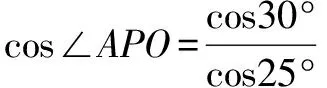
变式题5若异面直线a,b所成的角为50°，P为空间一定点，则过点P与a,b所成角都是80°的直线有( ).

A．一条 B.二条 C.三条 D.四条

同上法有四条.故选D.

年年岁岁花相似，岁岁年年题不同.考查这类空间角的大小是浙江省高考题中难以割舍的情结，其本质是考查线面角与面面角定义的合理性，是考查学生数学素养的有效途径.正是“初闻不知角中意，细品已是角中人，角中联系今犹在，挖掘内涵助提升.”

二、心里有谱，做题塌实

高考真题【2019年浙江高考21】如图，已知点F(1，0)为抛物线y2=2px(p>0)的焦点，过点F的直线交抛物线于A、B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧．记△AFG,△CQG的面积分别为S1,S2．

(1)求p的值及抛物线的标准方程；

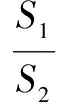
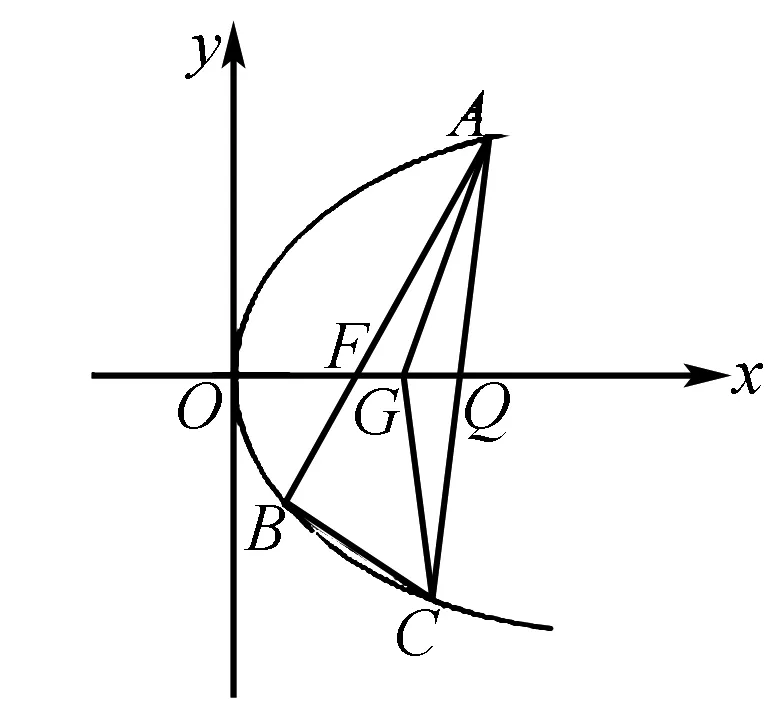
图4

题源揭秘：本题可借助抛物线焦点弦的性质求解.结合人教A版《数学》(选修2-1)第70页例5，第73页习题2.4A组第6题，第81页复习参考题B组第7题可得到抛物线的常用结论：已知抛物线y2=2px(p>0)上的两个动点A(x1,y1),B(x2,y2),

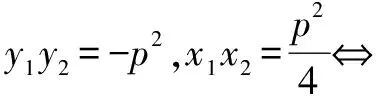
(3) 以AB为直径的圆与准线相切；

(6)过抛物线焦点F的直线交抛物线于A，B两点，通过点A和抛物线顶点的直线交抛物线的准线于点D，则直线DB平行于抛物线的对称轴．

(7)过抛物线焦点F的直线交抛物线于A，B两点，准线与x轴交于点E，则x轴平分∠AEB；反之，若x轴平分∠AEB，则直线过点F.

真题解答：

(2)设A(xA,yA),B(xB,yB),C(xc,yc)，重心G(xG,yG).令yA=2t,t≠0，则xA=t2.

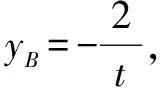
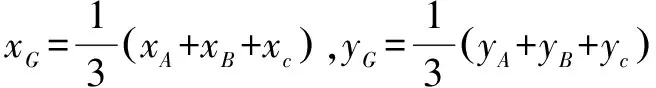
所以，直线AC方程为y-2t=2t(x-t2)，得Q(t2-1,0).

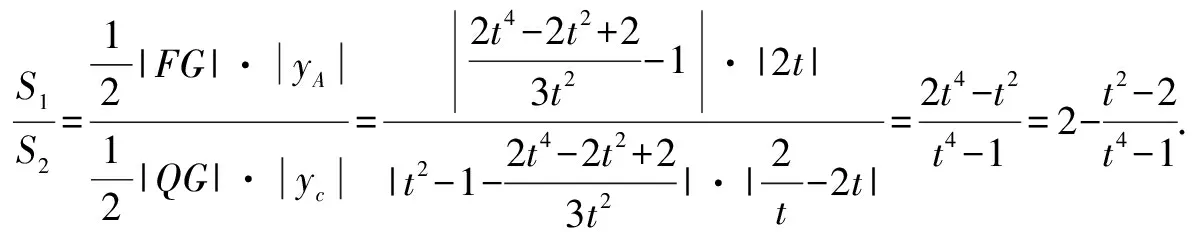
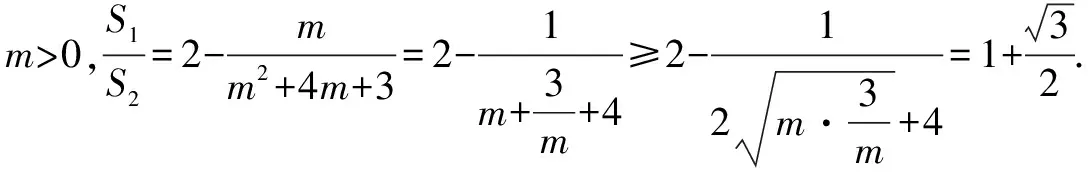
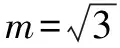
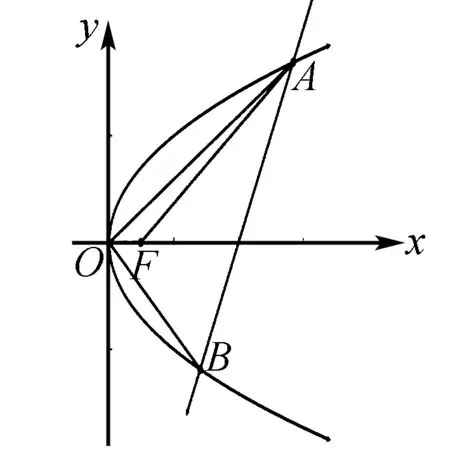
图5

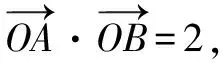
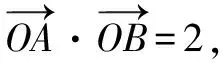
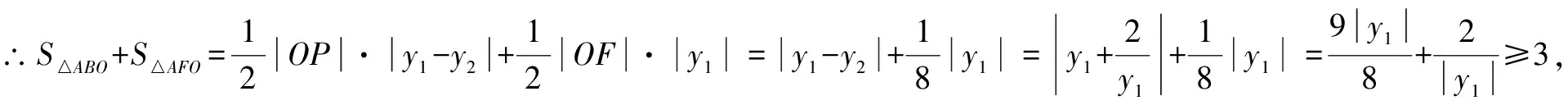
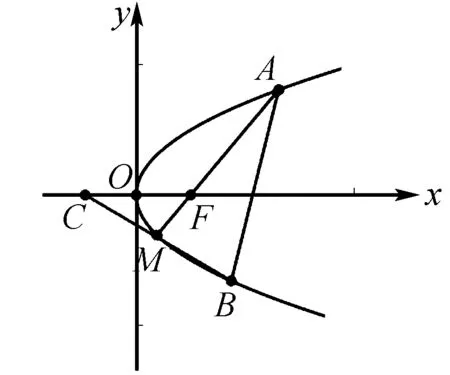
图6

变式2已知F为抛物线y2=x的焦点，过点F的直线AM交抛物线于A，M两点，过点M作直线BC交抛物线于B，交x轴于点C，若M为BC的中点，求|AB|的最小值.

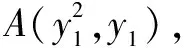
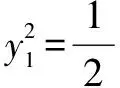
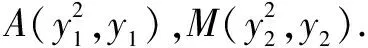
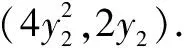
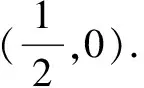
变式3(2001年全国卷)设抛物线y2=2px(p>0)的焦点为F，经过点F的直线交抛物线于A、B两点.点C在抛物线的准线上，且BC∥x轴．证明直线AC经过原点O.

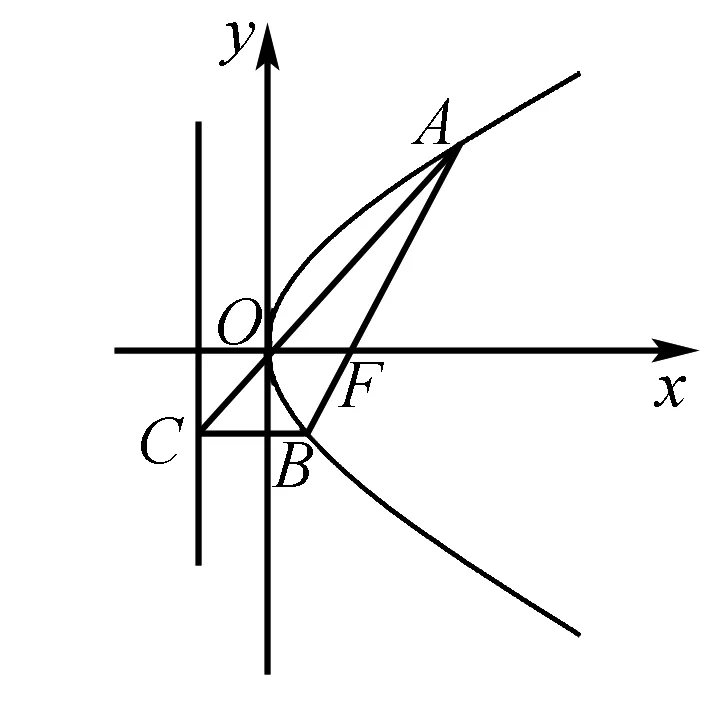
图7

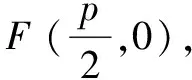
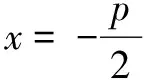
证明二如图8，记x轴与抛物线准线l的交点为E，过A作AD⊥l，D是垂足．则AD∥FE∥BC．

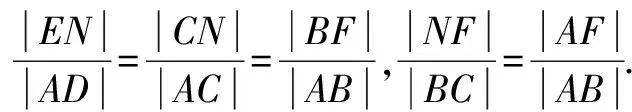
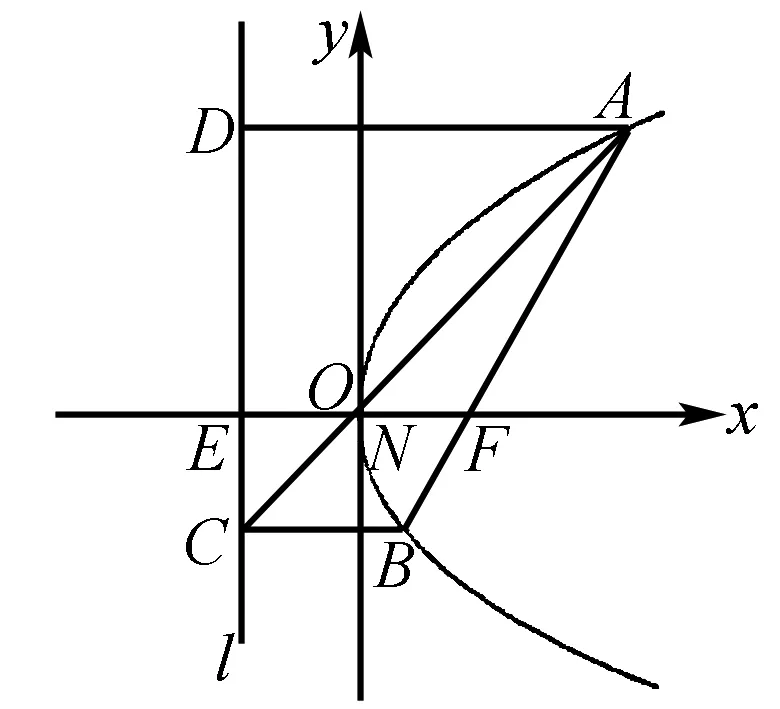
图8

根据抛物线的几何性质，|AF|=|AD|，|BF|=|BC|，

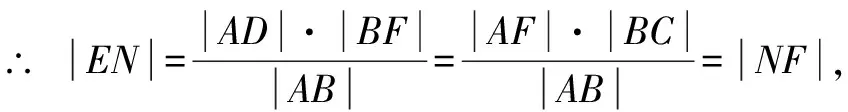
以上几道题都涉及多点关联的问题，而关联定乾坤的是抛物线的焦点弦性质(证明过程参照变式3)，心中有抛物线的常用结论，做题心里就有谱，踏实.抛物线中很多结论可推广到椭圆、双曲线，它们具有类似的性质.

我们在平时学习，高考复习期间，千万别忘了“本”，更不能舍本求末，课本中的“金矿”等待我们去挖掘！