数形结合思想在近年来高考中的应用

王昌林 徐 易

(四川省成都市四川师范大学附属第三实验中学 611331)

数形结合思想贯穿于整个高中数学，而且在各类数学问题中都隐含了数形结合思想.大量实践表明，打破学生的思维定势是数形结合思想在解题中的最大价值，能够帮助学生数学核心素养的养成，具体体现在以下几个方面：

1.培养和提高学生的直觉思维能力；

2.培养和提高学生的抽象思维能力；

3.培养和提高学生的辩证思维能力；

4.培养和提高学生的发散性思维能力；

5.培养和提高学生的创造性思维能力.

伴随着新课程标准的推行，在高考试题中出现了越来越多的需要用数形结合方法解决的题型，这个现象明确的说明了用数与形有效结合的方法能够提升学生的数学思维能力，可以帮助学生分析题意找到解题思路，进而达到高效的解题成果.

笔者将以近年来高考试题为蓝本，将数学结合思想在高考中的运用加以论述.

一、数形结合思想在集合中的应用

应用1 (2018年 全国Ⅱ卷(理) 第2题) 已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z}，则A中元素的个数为( ).

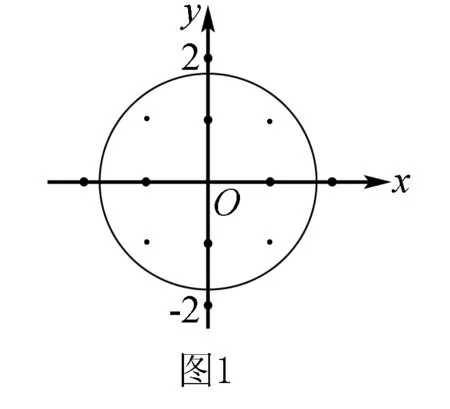
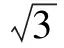
评注正确运用数形结合思想将问题转化，把集合的计算问题有效地转化为形象直观的图形，将集合语言转化为图形语言，在解题过程中应该尽量使用数形结合思想，可以提高数学解题的效率.

二、数形结合思想在函数中的应用

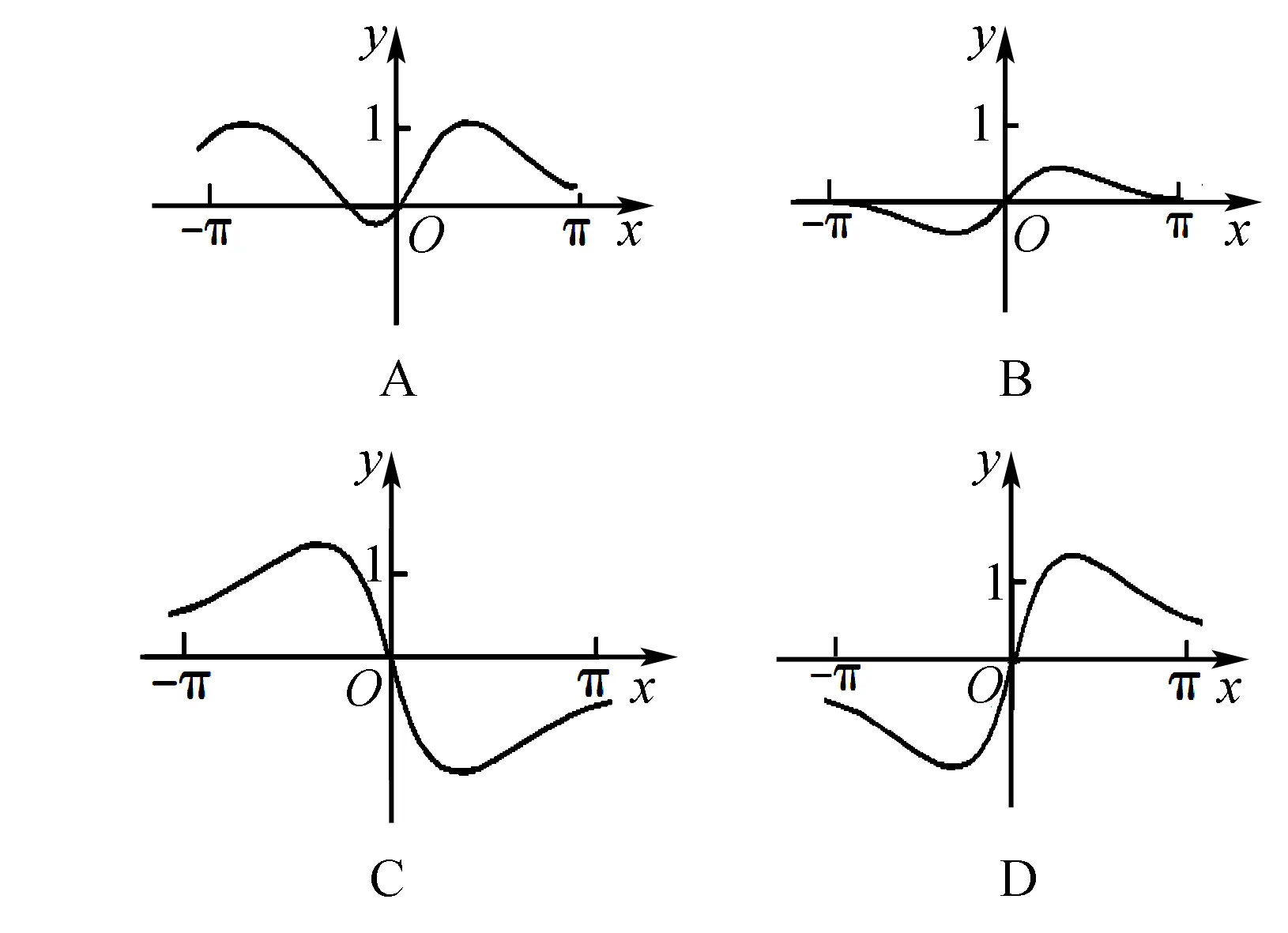
评注根据试题所给已知条件将式子进行奇偶性的判断，再利用数形结合思想解题.

三、数形结合思想在三角函数中的应用

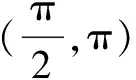
其中所有正确结论的编号是( ).

A.①②④ B.②④ C.①④ D.①③

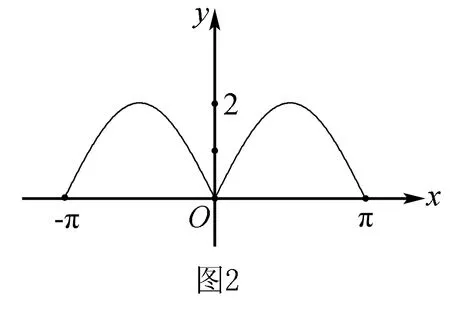
解析准确作出f(x)=sin|x|+|sinx|的函数图象(如图2所示)，则可根据图象得到结论①④正确.

评注本题运用数形结合的思想进行求解；在作出正确图象的前提下，再来看待本题中所需判断的4个结论也就变得直观与简单，答案都可直接从图3中找出，十分的快捷与准确.

四、数形结合思想在不等式中的应用

应用4(2019 北京卷(理) 第5题)若x，y满足|x|≤1-y，且y≥-1，则3x+y的最大值为( ).

A.-7 B.1

C.5 D.7

评注本题是常见的线性规划问题的基本题型，根据解决线性规划问题的“画、移、解”等一般步骤可以求解得到相应的解答.题目本身的难度不是很大，但是在没有图形的支撑的情况下进行求解还是比较的困难.

五、数形结合思想在平面向量中的应用

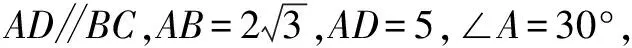
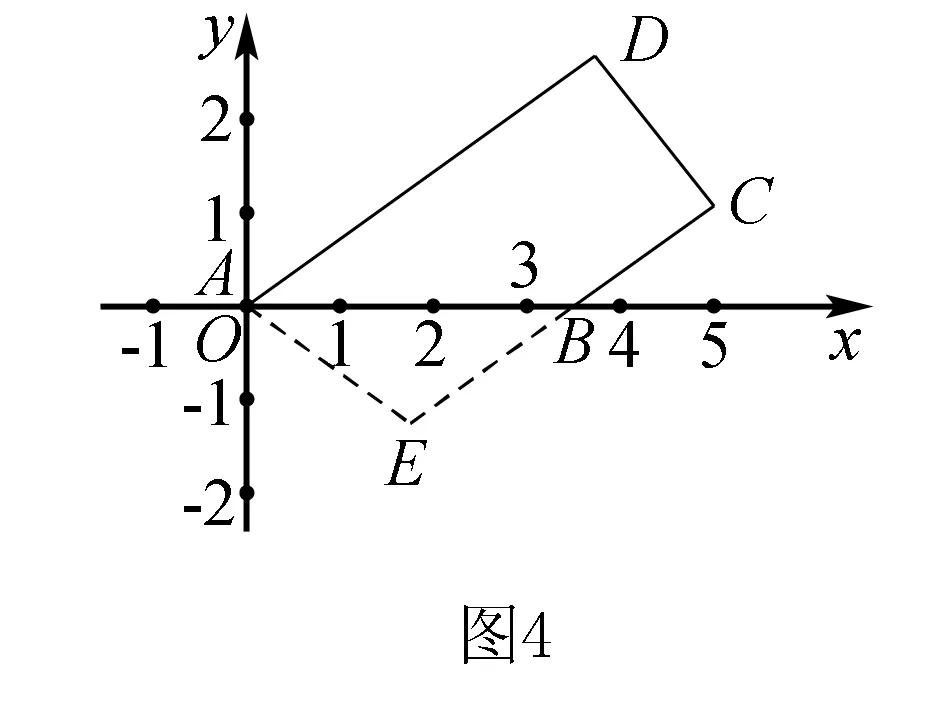
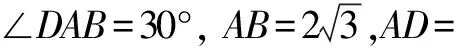
评注平面向量问题中，在便于建立坐标系的情况下，运用数形结合的思想，使用坐标法对问题进行求解更为直观快捷.

六、数形结合思想在数列中的应用

应用6(2019 北京卷(理) 第10题)设等差数列{an}的前n项和为Sn，若a2=-3，S5=-10，则a5为____；Sn的最小值为____.

评注数列是特殊的函数，它是由很多孤立的点构成的.所以在解决很多数列问题时都需要合理利用数形结合思想，对于数列最值问题如果只从数量关系去思考问题，很难找到解决问题的突破点，借助于图象单调性判断既形象又直观，而且还大大提高了解题的准确性.

七、数形结合思想在坐标系与参数方程中的应用

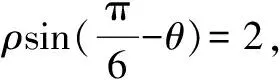
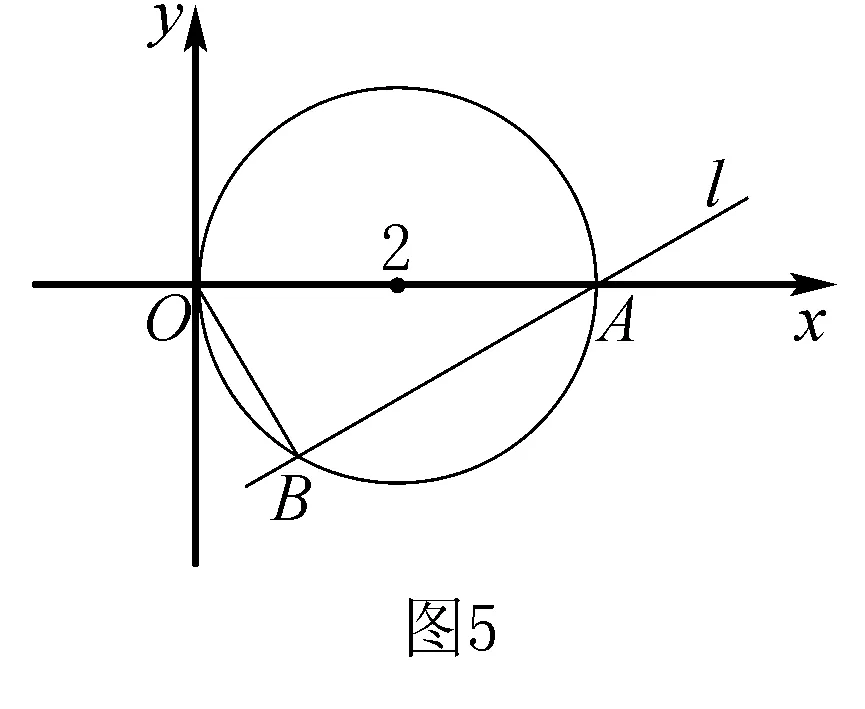
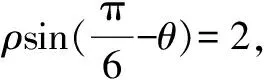
数形结合思想贯穿于整个高中数学，而且在各类数学问题中都隐含了数形结合思想.在具体的数学题中，利用数形结合思想解题，将困难的问题转化为容易的问题、将繁琐的问题转化为简单的问题、将抽象的问题转化为直观的问题等方式进行解题，达到事半功倍的解题效率.