一道模拟题 两个疑难点 三点教学启示

江秀梅 刘大明

(江西省抚州市第一中学 341100)

一、提出问题

下面试题是网络、教辅书籍、模拟试卷中经常引用的试题，考查知识点多，综合程度高，能力要求高的试题.教师在讲评此题时，存在思路混乱、讲解不到位的教学现象，甚至极容易犯科学性错误.

图1

试题如图1所示，将一轻质弹簧从物体B内部穿过，并将其上端悬挂于天花板，下端系一质量为m1=2.0kg的物体A.平衡时物体A距天花板h=2.4m，在距物体A正上方高为h1=1.8m处由静止释放质量为m2=1.0kg的物体B，B下落过程中某时刻与弹簧下端的物体A碰撞(碰撞时间极短)并立即以相同的速度与A运动，两物体不粘连，且可视为质点，碰撞后两物体一起向下运动，历时0．25s第一次到达最低点，(弹簧始终在弹性限度内，不计空气阻力，g=10m/s2)下列说法正确的是( ).

A．碰撞结束瞬间两物体的速度大小为2m/s

B．碰撞结束后两物体一起向下运动的最大位移大小为0.25m

C．碰撞结束后两物体一起向下运动的过程中，两物体间的平均作用力大小为18N

D．A、B到最低点后反弹上升，A、B分开后，B还能上升的最大高度为0.2m

原参考答案：ABC.

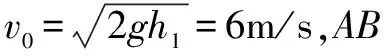
仔细分析此题，试题模糊了“平均作用力”的概念，答案是错误的，解析亦存在科学性错误，还存在分析不到位的现象.其中，这里对应于两个教学疑难点：(1)平均作用力问题；(2)连接弹簧的叠加体分离问题.下面就这两个疑难点，与同仁探讨交流，以期抛砖引玉.

二、疑难点：平均作用力

1.物理平均和数学平均

“平均”一词，内涵丰富，意义深刻，其意义时常困扰师生.首先要区分物理平均和数学平均两个概念.

(1)数学平均

数学平均，一般指统计平均，也是状态平均.例如，一个班的学生身高各异，把该班所有同学的身高数值加和后除以班级总人数，就得到了该班的平均身高.注意，学生的身高是独立的，相互不影响，是独立的“状态”.

(2)物理平均

物理平均，它不是简单地统计平均，而是一种过程平均.例如，小明20岁完全成熟，身高不再增长，最终身高是1.8m，问小明这20年里平均每年增高多少？答平均每年增高0.09m.显然，小明的身高增长具有累加性，不是独立的，对应一个增长过程，是一种过程平均.高中物理中，平均速度、平均加速度、平均功率等都是过程平均.不仅如此，未冠于“平均”头衔的众多物理概念，例如感应电动势、电场强度(从电势差角度看电场强度)、电流实际上都具有过程平均的意义.

2.过程平均的维度问题

同样一个过程，当我们对这一个过程的观察视角不同，就会有不一样的获得感.也就是，观察、评价、量化过程，还存在维度问题.再以小明的成长过程为例，前文关注的是身高维度，还可以关注体重维度，例如小明每年体重增加3kg.显然，多维度看小明的成长情况，能够较全面地评判其成长状况；各维度同属于同一过程，可能有一定关联性，但不失独立性，否则就属于同一维度.

3.平均作用力

从过程性来看，力有两个作用效果，一个是空间积累效应，一个是时间积累效应，前者用功来表示，量度了能量的变化(如动能定理)；后者用冲量来表示，量度了动量的变化(即动量定理).也就是说，量化力的平均作用效果，具有两个维度，一个是空间维度，一个是时间维度，因此讲“平均作用力”，必须强调观察维度.就空间维度，称之为位移平均作用力；就时间维度，称之为时间平均作用力.

(1)位移平均作用力

(2)时间平均作用力

(3)从特例中看两个平均作用力

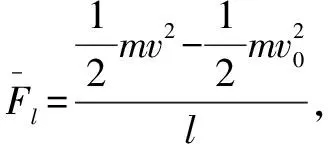
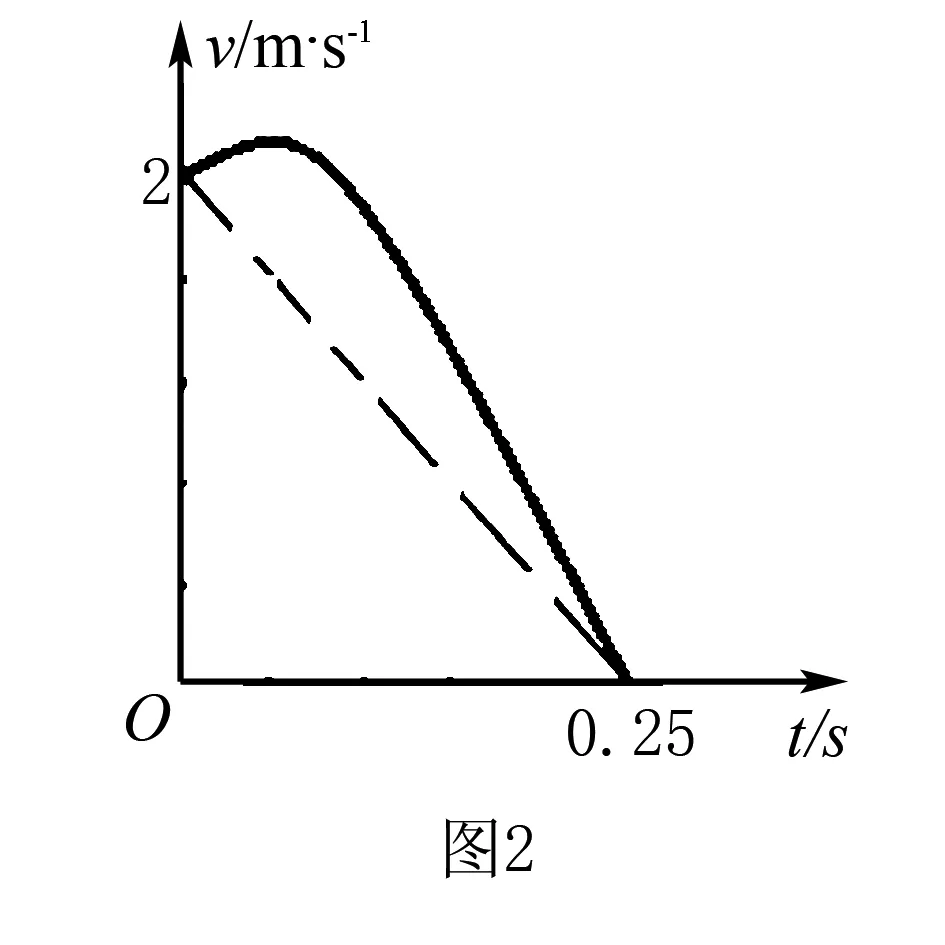
(4)回评试题

三、疑难点：连接弹簧的叠加体分离问题

连接弹簧的叠加体分离问题是教学中一个难点，绝大多数教师和教辅资料仅仅注意到了分离的临界条件，却忽视了分离的前提条件.于是在教学或试题命制中，极容易犯科学性错误，我们认为，命题或解答此类题型,先根据临界条件确定分离位置,再由分离位置确证前提条件,是一条必经之路.

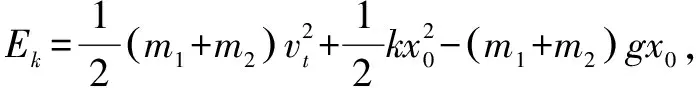
四、教学启示

关于教学原则的讨论由来已久，尽管不同学者的表述不尽相同，但核心意义基本上一致，例如直观性原则、可接受性原则、科学性原则、循序渐进原则、教育性原则等等.通过对上面试题的深度反思，我们依然可以获得三点教学启示：

1、只有教研“深入”，才能讲解“浅出”

平均作用力问题、连接弹簧的叠加体分离问题均是教学中的难点，绝大多数教师和教辅书籍对两个问题的研究不够深入，于是在命制试题和教学中，时常犯科学性错误，也经常出现讲解不到位的现象.教研不“深入”，讲解难“浅出”.

2.只有讲解“通俗”，才能达成“易懂”

数学上的统计平均是学生前期获得的知识，这一知识作为前概念，时常成为物理平均学习的障碍.因此，讲清楚数学平均和物理平均的区别，是突破前概念的障碍性影响(负向作用)的不二法门.然而，要讲清楚两者的区别不容易.我们认为，讲解时用生活化的例子作为引子，才能帮助学生突破思维障碍.讲解不“通俗”，理解难“易懂”.

3.只有思维“发散”，才能知识“聚焦”

要理解位移平均作用力和时间平均作用力的区别，就概念讲概念，那么很难聚焦核心知识或核心内涵——平均作用力的概念需要从空间和时间两个维度去理解.讲解概念后，补充特例分析，再以试题为例，配合图像分析，就能理解两个平均作用力的区别与联系了.思维不“发散”，知识难“聚焦”.