可控弯接头导向控制理论研究

张光伟，刘英海

(西安石油大学 机械工程学院，陕西 西安 710065)



可控弯接头导向控制理论研究

张光伟，刘英海

(西安石油大学 机械工程学院，陕西 西安 710065)

提出了一种动态偏置指向式旋转导向钻井工具的工具角与工具面角调节的控制方法。通过建立运动学模型，分别对钻井工具的工具角调节方法与工具面角调节方法进行了理论论证，并将2种不同参数的调节方法加以合并，对导向工具的整个控制过程进行分析，提出3种对可控弯接头工具角与工具面角的控制方式，利用MATLAB软件分别对工具角和工具面角调节过程进行轨迹仿真。研究实现了导向工具根据工作需要对工具角和工具面角的灵活调节，并且在工具角与工具面角调节完成后使整个系统处于稳定状态。

旋转导向钻井；可控弯接头；工具角调节；工具面角调节

张光伟,刘英海.可控弯接头导向控制理论研究[J].西安石油大学学报(自然科学版)，2016，31(3):110-115.

ZHANG Guangwei,LIU Yinghai.Theoretical research of controllable sub steering control[J].Journal of Xi'an Shiyou University(Natural Science Edition),2016,31(3):110-115.

引　言

近年来，非常规油气田开发的战略地位日益凸显。凭借非常规油气资源的开发，美国达到开采标准的油气资源储量跃升到世界首位，它已从原油进口国变为原油出口国[1-6]。旋转导向钻井技术是20世纪90年代兴起的一项尖端自动化钻井技术，是非常规油气田开发的必备技术。旋转导向钻井工具按照其导向工作方式分为推靠式(push-the-bit)与指向式(point-the-bit)，按照其在工作状态下导向机构是否静止分为静态偏置式(static-bias)与动态偏置式(dynamic-bias)，其中动态偏置指向式旋转导向钻井工具至今没有被开发出来[7-10]。工具角与工具面角的调节与保持是动态偏置指向式旋转导向钻井工具的难点。为此，本文提出一种工具角与工具面角的控制方法。

1　可控弯接头导向机构组成

可控弯接头导向机构(见图1)通过改变旋转外套、外偏心环和内偏心环的相对位置，产生偏心矢量和相位，改变导向轴的空间姿态，实现可控弯接头工具角和工具面角的调整[11]。内、外偏心环组由偏心环组驱动系统提供转速，设外偏心环速度为ω1，内偏心环速度为ω2，旋转外套速度由顶驱系统提供且与内、外偏心环组速度相反，记为ω3，如图2所示。

图1　可控弯接头导向机构简图Fig.1　Controllable bent sub steering mechanism diagram

图2　偏心结构示意图Fig.2　Eccentric structure diagram

2　偏心结构运动学模型的建立

为了方便数学方程的建立，首先对整个偏心机构进行分析，外偏心环与旋转外套的几何中心皆为O，内偏心环几何中心O1，导向轴在偏心结构处几何中心O2，内偏心环与外偏心环偏心距均为e。根据上述几何结构特点建立平面杆系模型，如图3所示。

根据图3所示几何关系建立数学方程，可以求得导向轴的几何中心O2在任意一时刻t的坐标O2(x,y)，导向轴在偏心结构处的几何中心偏离弯接头几何中心的距离即导向偏心距ρ，也就是OO2。导向偏心距ρ与x轴之间的夹角为θ，整个偏心机构以速度ω3转动，OO2实际转过的工具角γ为θ减去ω3t，因而有：

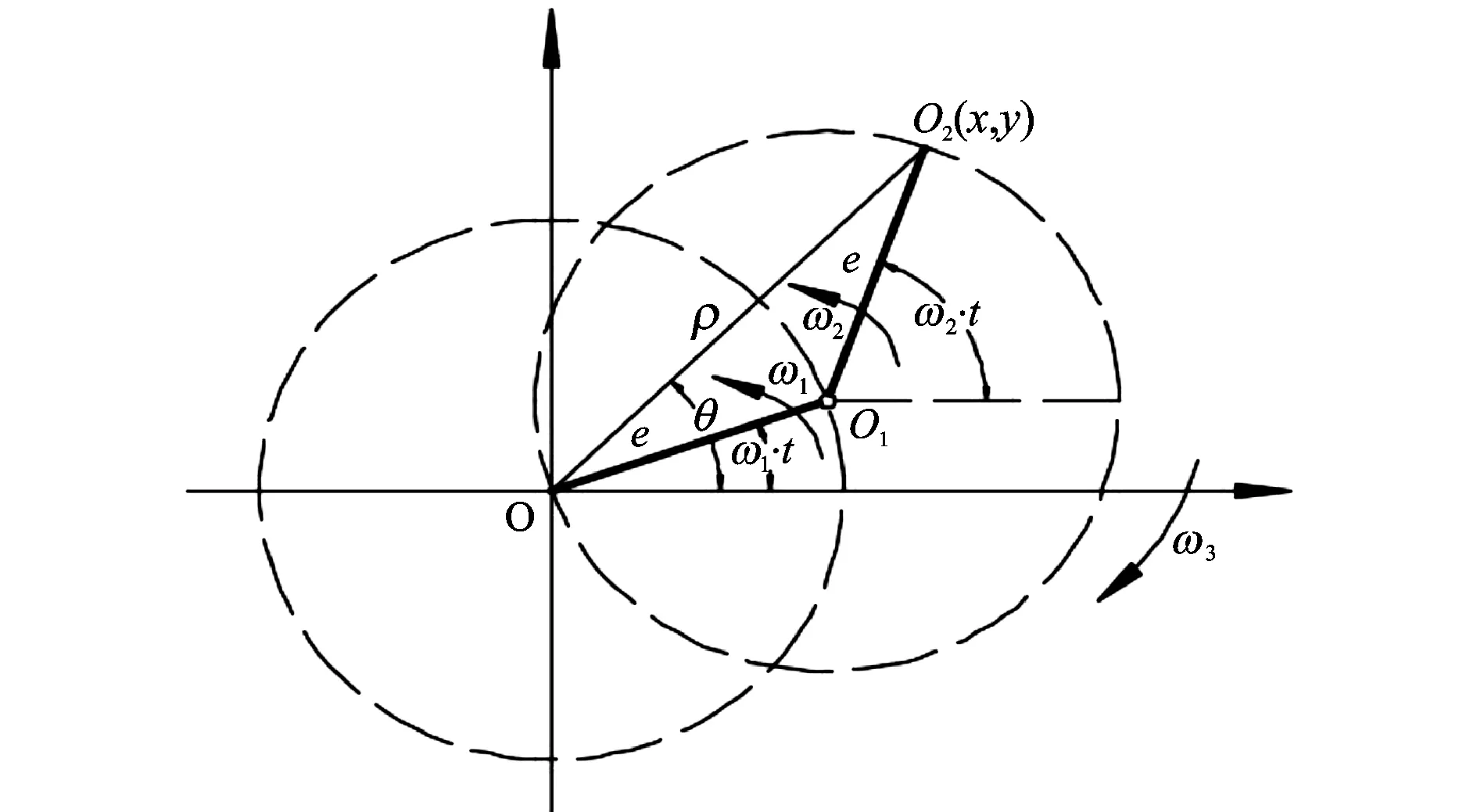
图3　偏心结构运动模型图Fig.3　Motion model diagram of the eccentric structure

x=e[cos(ω1t)+cos(ω2t)]，

(1)

y=e[sin(ω1t)+sin(ω2t)]，

(2)

ρ2=e2[cos(ω1t)+cos(ω2t)]2+e2[sin(ω1t)+sin(ω2t)]2=2e2[1+cos(ω2t-ω1t)]，

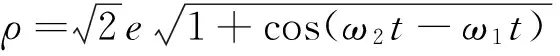
(3)

因为OO1O2所构成的三角形为等腰三角形，所以：

(4)

则工具面角

(5)

式中：ρ为导向偏心距，mm；γ为工具面角，rad；e为内、外偏心环偏心距，mm；ω1为外偏心环角速度，rad/s；ω2为内偏心环角速度，rad/s；ω3为旋转外套角速度，rad/s；θ为导向轴偏心距ρ与x轴之间的夹角，rad；t为时间，s。

由式(3)和式(5)可知，导向偏心距ρ只与偏心距e和内、外偏心环角速度相关；工具面角γ与旋转外套，内、外偏心环角速度相关。本文所述导向机构的工具角连续调节功能是通过间接调节钻头的偏心距ρ来实现的，连续调节工具面角γ只需直接调节其大小即可。

当工具角调节到预定位置处时，接下来就必须研究如何让工具角稳定到该位置。对ρ关于t求导得

(6)

dρ/dt的值为ρ在单位时间内的增量，要使ρ稳定在某一值处，其增量dρ/dt的值要恒等于零。要dρ/dt恒等于零，必有：

(ω1-ω2)t=nπ，

(7)

或ω1-ω2=0。

(8)

上式中n为整数。

式(7)是与时间t有关的稳定状态，是一种瞬时稳态并不能满足实际工作需求；式(8)的稳定状态与时间无关，是一个持续稳定状态，满足实际工作需要。因此要使工具角随时间保持不变，必有ω1=ω2。

进一步对导向偏心距ρ具体稳定在哪一值处做进一步的论证。设再经过t1时间，导向偏心距为ρ1，O2坐标为(x1,y1)，OO1转过的工具角为(ω1t1+ω1t)，O1O2转过的工具角为(ω1t1+ω2t)。则：

x1=ecos(ω1t1+ω1t)+ecos(ω1t1+ω2t)，

(9)

y1=esin(ω1t1+ω1t)+esin(ω1t1+ω2t)，

(10)

(11)

此时ρ=ρ1，可以看出导向偏心距ρ稳定在ω1=ω2时的值。

在进行工具面角调节时，当工具面角到达预定位置时也需要将其稳定在预定位置处。与工具角调节所用方法相同，也从其增量入手，即对工具面角γ关于t进行求导得

(12)

dγ/dt是γ在单位时间内的增量，要使γ的值保持不变，则dγ/dt的值必须恒等于零。那么：

(13)

当(ω1+ω2)/2=ω3后，随着时间的推移，γ值恒定。接下来对上述论证做进一步的研究分析，从数学角度证明该方案的可行性。设工具面角调节完成后外偏心环速度为ω11，内偏心环速度为ω21，旋转外套的速度为ω31，且此时有(ω11+ω21)/2=ω31，经过时间t2，此时工具面角为γ1。则有：

(14)

式中：ω11为工具面角调节完成后外偏心环角速度，rad/s；ω21为工具面角调节完成后内偏心环角速度，rad/s；ω31为工具面角调节完成后旋转外套角速度，rad/s。

由上式可以看出工具面角γ稳定在(ω1+ω2)/2=ω3时的位置。

因此，要使ρ、γ同时稳定在某一工具角与工具面角处时必有:ω1=ω2=ω3。

3　可控弯接头控制方法

根据上述研究可知，该种控制方案实现弯接头连续工具角调节与工具面角调节共有以下3种途径：(1)先调节工具角，后调节工具面角；(2)先调节工具面角，后调节工具角；(3)工具面角与工具角同时调节。

3.1先调节工具角后调节工具面角

先进行工具角调节，即对导向偏心距ρ的大小先进行调节，可以通过(ω2t-ω1t)的差值实现连续调节。单位时间内调节的初始变量等于(ω2-ω1)，从调工具角公式可以看出导向偏心距ρ具有周期性。则：

(ω2-ω1)/2π=n+α。

(15)

式中：n为整数； α为单位时间内工具角调节初量，rad/s。

为了便于分析，取n=0，随着时间的增加ρ值在0～2e之间连续变化，通过调节单位时间内工具角调节初量α的值实现工具角调节的快慢。当工具角到达预定工作位置后立刻使ω1=ω2，随后工具角稳定在预先设定值保持不变。

随后进行工具面角调节，当工具角调节完成后即有ω1=ω2，此时在调节工具面角的同时需保持所调好的工具角保持不变，对内、外偏心环角速度同时调节相同的量。

此时ω1=ω2，所以γ=t(ω1+ω2)/2-ω3t就变成了γ=ω1t-ω3t，单位时间内工具面角变化量为(ω1-ω3)，由于系统作圆周运动所以工具面角γ也具有周期性。因此：

(ω2-ω3)/2π=n+β。

(16)

式中：n为整数；β为单位时间内工具面角调节量，rad/s。

同样为了便于分析，取n=0，当改变单位时间内偏心环组相对于旋转外套转过的工具面角β时，随着时间的增加偏心环组以β为步长可到达任一指定工具面角。调节工具面角到达工作位置后立即使ω1=ω3，即可将工具面角稳定到该位置处。

3.2先调节工具面角后调节工具角

该方法先通过旋转外套与内、外偏心相对角位移实现工具面角的调节。根据工具面角调节公式设定初始值，使系统以特定的速度进行工具面角的调节，达到预定位置后立即使ω1+ω2=2ω3，实现工具面角调节。接着通过内、外偏心角速度的微调实现工具角调节，在调节过程中始终保持ω1+ω2=2ω3，当工具角到达预定位置立即使ω1=ω2=ω3，整个调节过程结束。

3.3工具角与工具面角同时调节

工具角调节过程与工具面角调节过程遵循各自的调节规律。实现工具角与工具面角同时调节就必须将二者的调节过程统一协调起来，这个过程就必须在ω1、ω2、ω3之中选一个速度基准，其余2个速度根据工作需要以基准速度为参考点进行工具角和工具面角的调节。无论将哪一个速度定为基准速度，其调节方式都遵循工具角调节公式与工具面角调节公式。在实际钻井过程中导向转速就是破岩转速，在本文中导向转速即为旋转外套转速ω3，所以将ω3定为速度基准进行分析。外偏心环角速度ω1与内偏心环角速度ω2以旋转外套角速度ω3为基准进行调节。为便于控制整个调节过程，令(ω1-ω2)与(ω1+ω2)/2-ω3保持不变。若工具角与工具面角同一时间调节到工作位置，导向完成。若工具角先调节好，则接下来参照第一种调节方法进行工具面角调节，直至调节完成；若工具面角先调节好，参照第二种调节方法调节工具角，直至弯接头到达工作位置。

4　可控弯接头导向控制仿真及分析

下面通过MATLAB分别对工具角调节过程与工具面角调节过程进行仿真比较。为了便于仿真分析，公式(15)、(16)中均取n=0，并根据第一种调节方式进行调节。令在工具角调节时，工具面角单位时间内调节量为β1，其值等于(ω1+ω2)/2-ω3；工具角调节完成后就有ω1=ω2，工具面角单位时间内调节量为β2，其值等于ω2-ω3。工具角与工具面角调节仿真时用到的6组数据见表1。在仿真过程中将这6组数据再分为a、b、c与d、e、f两组进行仿真对比。在数组a、b、c中α、β1、β2对应相等，数组d、e、f中α、β1、β2对应不等。

表1　仿真数据

4.1可控弯接头工具角调节仿真分析

分别用数组a、b、c与d、e、f进行工具角调节仿真，图4(a)与图4(b)为数组a、b、c的仿真结果，图4(a)工具角调节时间16 s，总调节时间30 s；图4(b)工具角调节时间85 s，总调节时间90 s。图4(c)与图4(d)为数组d、e、f的仿真结果，图4(c)工具角调节时间16 s，总调节时间30 s；图4(d)工具角调节时间85 s，总调节时间90 s。从图4可以看出，工具角调节具有周期性，当工具角调节完成后就稳定在某一值处。且工具角的调节与外偏心环角速度ω1、内偏心环角速度ω2、旋转外套角速度ω3无直接关系，单位时间内工具角调节初量α相等时其工具角调节量相同。单位时间内工具角调节初量α越大，单位时间内工具角调节量越大，但调节过程越不平稳；单位时间内工具角调节初量α值越小，单位时间内工具角调节量越小，而调节过程更趋于平稳。

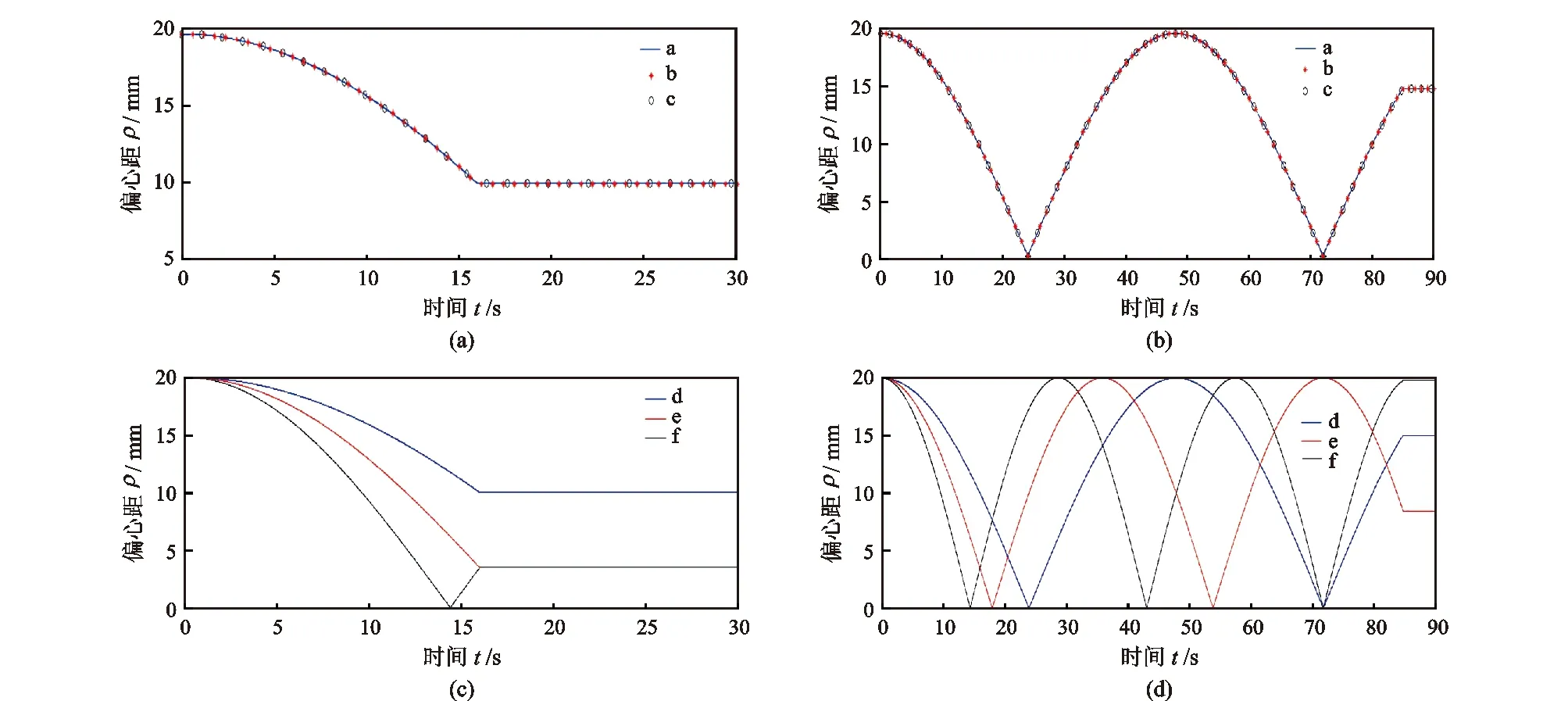
图4　工具角调节仿真图Fig.4　Tool angle adjustment simulation

4.2可控弯接头工具面角调节仿真分析

分别用数组a、b、c与d、e、f进行工具面角调节仿真，图5(a)与图5(b)为数组a、b、c的仿真结果，图5(a)工具角与工具面角同时调节时间16 s，只工具面角调节时间28 s，总调节时间30 s；图5(b)工具角与工具面角同时调节时间16 s，只工具面角调节时间115 s，总调节时间120 s。图5(c)与图5(d)为数组d、e、f的仿真结果，图5(c)工具角与工具面角同时调节时间16 s，只工具面角调节时间28 s，总调节时间30 s；图5(d)工具角与工具面角同时调节时间16 s，只工具面角调节时间115 s，总调节时间120 s。从图5可以看出，当工具面角调节完成后就稳定在某一值处。且工具面角的调节与外偏心环角速度ω1、内偏心环角速度ω2、旋转外套角速度ω3无

图5　工具面角调节仿真图Fig.5　Tool face angle adjustment simulation

直接关系，单位时间内工具面角调节量β相等时其工具面角调节量相同。工具面角调节与单位时间工具面角调节量β值有关，β值越大，单位时间工具面角调节量越大；β值越小，单位时间工具面角调节量越小。

5　结论

(1)提出一种基于动态偏置指向式旋转导向钻井工具控制方式，在理论上是可行的。

(2)工具角的调节具有周期性且与外偏心环速度ω1、内偏心环速度ω2、旋转外套速度ω3的大小无直接关系，与单位时间内工具角调节初量α有关。α值越大，单位时间内工具角调节量越大，但调节过程越不平稳；α值越小，单位时间内工具角调节量越小，而调节过程越平稳。

(3)工具面角调节与单位时间工具面角调节量β值有关，β值越大，单位时间工具面角调节量越大；β值越小，单位时间工具面角调节量越小。当工具面角调节完成后，工具面角稳定在某一值处。

(4)工具角与工具面角的调节都具有周期性，当可控弯接头处于稳定状态时必有ω1=ω2=ω3。

[1]刘新华，董广华，赵洪山，等.旋转导向井下工具控制系统设计及室内试验[J].石油钻探技术，2011,39(5)：86-90.

LIU Xinhua,DONG Guanghua,ZHAO Hongshan,et al.Design and laboratory test of control system for rotary steering motor[J].Petroleum Drilling Techniques,2011,39(5):86-90.

[2]郭晓霞，杨金华，钟新荣.北美致密油钻井技术现状及对我国的启示[J].石油钻采工艺，2014,36(4)：1-5,9.

GUO Xiaoxia,YANG Jinhua,ZHONG Xinrong.The status of tight oil drilling technique in North America and its enlightenment to China[J].Oil Drilling & Production Technology,2014,36(4):1-5,9.

[3]姜伟，蒋世全，盛利民，等.旋转导向钻井工具系统的研究及应用[J].石油钻采工艺，2008,30(5)：21-24.

JIANG Wei,JIANG Shiquan,SHENG Limin,et al.Research on rotary navigation drilling tools and its application[J].Oil Drilling & Production Technology,2008,30(5):21-24.

[4]苏义脑，窦修荣，王家进.旋转导向钻井系统的功能、特性和典型结构[J].石油钻采工艺，2003,25(4)：5-7.

SU Yinao,DOU Xiurong,WANG Jiajin.Functions,characteristics and typical configurations of rotary steerable drilling system[J].Oil Drilling & Production Technology,2003,25(4):5-7.

[5]赵金洲，孙铭新.旋转导向钻井系统的工作方式分析[J].石油机械，2004,32(6)：73-75.

ZHAO Jinzhou,SUN Mingxin.Analysis of the working mode of the rotary steering drilling system[J].China Petroleum Machinery,2004,32(6):73-75.

[6]李俊，倪学莉，张晓东.动态指向式旋转导向钻井工具设计探讨[J].石油矿场机械，2009,38(2)：63-66.

LI Jun,NI Xueli,ZHANG Xiaodong.Approaching of dynamic point-the-bit rotary steering drilling tool[J].Oil Field Equipment,2009,38(2):63-66.

[7]孙铭新.旋转导向钻井技术[M].东营:中国石油大学出版社，2009.

[8]雷静，杨甘生，梁涛，等.国内外旋转导向钻井系统导向原理[J].探矿工程(岩土钻掘工程)，2012,39(9)：53-58.

LEI Jing,YANG Gansheng,LIANG Tao,et al.Principles of domestic and rotary steerable drilling system[J].Exploration Engineering(Rock & Soil Drilling and Tunneling),2012,39(9):53-58.

[9]李超，于佐军.动态指向式旋转导向钻井系统的虚拟现实仿真[J].自动化与信息工程，2013,34(2)：37-40,45.

LI Chao,YU Zuojun.The virtual reality simulation of dynamic Point-the-Bit rotary steerable drilling system[J].Automation & Information Engineering,2013,34(2):37-40,45.

[10] 张光伟，李钊，游莉.可控弯接头变异万向轴和轴承的强度模拟分析[J].石油机械，2014,42(5)：25-28.

ZHANG Guangwei,LI Zhao,YOU Li.Strength simulation analysis of the variation cardan shaft and bearing on controllable bent sub[J].China Petroleum Machinery,2014,42(5):25-28.

[11] 王可可.井下闭环可控弯接头的设计和仿真分析[D].西安：西安石油大学，2013：20-21.

责任编辑：董瑾

Theoretical Research of Controllable Sub Steering Control

ZHANG Guangwei,LIU Yinghai

(College of Mechanical Engineering,Xi'an Shiyou University,Xi'an 710065,Shaanxi,China)

An adjustment and control method for the tool angle and the tool face angle of dynamic offset point-to-bit rotary steering drilling tool was put forward,and it was theoretically demonstrated through establishing the kinematic model of the eccentric structure.Three adjustment and control ways of the tool angle and the tool face angle of the controllable sub were proposed through the combination of two types of parameter adjustment ways and the analysis of the whole control process of the steering tool.The adjustment trajectories of the tool angle and the tool face angle are simulated using MATLAB software,and it is shown that to use the adjustment and control method can realize the flexible adjustment of the tool angle and the tool face angle of the steering tool according to need,and the whole system is in stable state after the tool angle and tool face angle adjustment is completed.

rotary steering drilling;controllable sub;tool angle adjustment;tool face angle adjustment

2015-07-10

国家自然科学基金“井下闭环可控弯接头导向机构基础理论研究”(编号：51174164)

张光伟(1961-)，男，教授，主要从事旋转导向钻井工具方面的研究。 E-mail：zhang-guangwei@163.com

10.3969/j.issn.1673-064X.2016.03.018

TE921

1673-064X(2016)03-0110-06

A