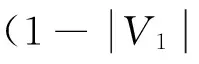一类串图的1-维魔幻标号
姚 明,姚 兵,赵振学
(1.兰州石化职业技术学院 信息处理与控制工程系,甘肃 兰州 730060; 2.西北师范大学 数学与统计学院,甘肃 兰州 730067)
一类串图的1-维魔幻标号
姚 明1,姚 兵2,赵振学1
(1.兰州石化职业技术学院 信息处理与控制工程系,甘肃 兰州 730060; 2.西北师范大学 数学与统计学院,甘肃 兰州 730067)
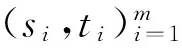
k-维(s,t)-魔幻全标号;魔幻全标号;对偶标号;全魔幻空间;向量空间
姚明,姚兵,赵振学.一类串图的1-维魔幻标号[J].西安石油大学学报(自然科学版),2016,31(3):122-126.
YAO Ming,YAO Bing,ZHAO Zhengxue.1-Dimension magical lablings of string graphs[J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(3):122-126.
引 言
1 预备知识
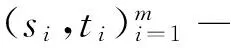
定义1设G是二部分(p,q)-图,如果存在一个整数对(s,t)(s,t≠0)和一一映射f:V(G)∪E(G)→[1,p+q],使得每一条边xy∈E(G),满足f(x)+f(y)=s+tf(xy),则称f为图G的一个(s,t)-魔幻全标号。图G是(s,t)-魔幻全标号图。此外,若(V1,V2)是G的二部划分,且对x∈V1,y∈V2,有maxf(V1(G)) 定义3令N为全体整数集合。设二部分(p,q)-图G有一个集合P(G)={(s,t)|s,t∈N,t≠0},若 (1)对任意的一个整数对(s,t)∈P(G),总存在G的一个一一映射f(s,t):V(G)∪E(G)→[1,p+q],使得每条边uv∈E(G),满足f(s,t)(u)+f(s,t)(v)=s+tf(s,t)(uv); (2)图G的任何一个(s′,t′)-魔幻全标号满足(s′,t′)∈P(G); 则称P(G)为G的全魔幻空间。此外,对固定的t0≠0有全魔幻子空间P(G,t0)⊂P(G)。 定义4令N为全体整数集合,n,m∈N,1≤m≤n。设二部分(p,q)-图G有一个m维向量的非空集合Γ(G),若集合Γ(G)对于加法及数乘2种运算封闭,则称集合Γ(G)为G的向量空间。此外,对固定的t∈N,t≠0,(s,t)∈P(G,t)⊂P(G),称Γ(G,t)⊂Γ(G)为G的向量子空间。 定义5设G是一个二部分(p,q)-图G,如果存在一个映射f:V(G)→[0,2p-3],使得f(E(G))=[1,2p-3]O,则称f为图G的一个奇优美标号,称G为奇优美图[12]。 例1.找(19μ,18μ+μ-1)-图G与(25μ,24μ+μ-1)-图R满足定义3 的整数对(s,t)。借助计算机搜索,结果如下: (19μ,18μ+μ-1)—图G (s1,t1)t1=-1(48,-1)(95,-1)(189,-1)(377,-1)(753,-1)…S1=2p+q×2n-1(s2,t2)t2=1(-9,1)(-19,1)(-39,1)(-79,1)(-159,1)…S2=1-10×2n-1︙︙︙︙︙︙︙︙︙ (25μ,24μ+μ-1)-图R (s1,t1)t1=1(-10,1)(-21,1)(-43,1)(-87,1)(-175,1)…S1=1-11×2n-1(s2,t2)t2=-1(65,-1)(129,-1)(257,-1)(513,-1)(1025,-1)…S2=2p+14×2n-1+1︙︙︙︙︙︙︙︙︙ 由定义3,显然有引理1: 引理1设二部分(p,q)-图G有全魔幻空间P(G),则对固定的t∈N,t≠0有全魔幻子空间P(G,t)⊂P(G),对任意的整数对(s,t)∈P(G,t)(i∈[1,m])有f(s,t),1,f(s,t),2,…,f(s,t),i。 由定义3,引理1有引理2: 证明:由引理1,对任意的整数对(si,t)∈P(G,t)(i∈[1,m])有f(s,t),1,f(s,t),2,…,f(s,t),i。由定义3,对固定的t及任意整数对(s,t)∈P(G),有f(s,t)(u)+f(s,t)(v)=s+tf(s,t)(uv);因此s=f(s,t)(u)+f(s,t)(v)-tf(s,t)(uv)。由等式知,对固定的t,对每一个不同的f(s,t),就有一个不同的s;为叙述方便,设函数F(s,t),i=si=f(s,t)(u)+f(s,t)(v)-tf(s,t)(uv);并令向量β,αi={si}={F(s,t),i}∈Γ(G,t),向量组B为:α1,α2,…,αi,β。注意到 αi+1={si+1}=si+2i-1s1-2i-1={si}+2i-1{s1}-{2i-1}, 即存在整数0≠2i-1=h∈N和向量β={h}∈Γ(G,t),使得 αi+1-αi-hα1+β=0。 根据定义4及引理1,有引理3: 引理3设二部分(p,q)-图G有向量空间Γ(G),并对固定的t∈N,t≠0有1 由定义2、3、4,和引理2有引理4: 引理4设二部分(p,q)-图G有 有超级强-魔幻全标号f(s,-t),且p≥3M=p+q+1。 (1)如果θ=s-tM,则(θ,t)∈P(G,t),其中s,t,θ∈N,s,t,θ≠0。 (2)如果对于α(θ,t)∈Γ(G,t),β(s0,t0)∉Γ(G,t),有α(θ,t)+tβ(s0,t0)=α(s,-t)成立,则存在最小正整数k,使得图G为-维(θ,t)-魔幻图,其中s0,t0∈N,s0=M,t0≥1。 证明:(1)因图G有魔幻全标号f(s,-t),所以(s,-t)∈P(G,t),由引理有α(s,-t)∈Γ(G,t)。构造G的一个标号函数g,注意到g(uv)=M-f(uv),uv∈E(G);g(u)=f(u),u∈V(G)。又 g(u)+g(v)=f(u)+f(v)=s-tf(uv)=θ+tM-t(M-g(uv))=θ+tg(uv),由定义1,3 有(θ,t)∈P(G,t);又f(s,-t)(V(G))=[1,p],maxf(V2(G)) (2)设(s0,t0)∈P(G,t),讨论情形如下: (1)对于α(θ,t),因si-θi=tMi(i∈[1,m])。有 α(θ,t)={θ1,θ2,…,θm}={s1-tM1,s2-tM2,…,sm-tMm} ={s1,s2,…,sm}-t{M1,M2,…,Mm} ={s1,s2,…,sm}-t{3p1,3p2,…,3pm} 由引理3,有α(s,-t)={s1,s2,…,sm},令β(s0,t0)={3p1,3p2,…,3pm},这里β(s0,t0)∈Γ(G,t0);因此 α(s,-t)+tβ(s0,t0)=α(s,-t)。 下面给出用具有1-维-魔幻全标号的二部分(p,q)-图G来构造大规模的1-维-魔幻全标号图的方法和关于二部分(p,q)-图G的1-维(s,t)-魔幻全标号的某些结果。 定理5 1:若(s,t)∈P(G),且s′=s+tM,则(s′,-t)∈P(G),其中M=2p+q+1,t≥1。 2:若(s,t)∈P(G),则G有一个奇优美标号。 证明:(1)由定义3,对于图G的每一条边xy∈E(G),总有f(x)+f(y)=s+tf(xy),因此 f(x)+f(y)=s+tf(xy)=s′-tM+tf(xy)=s′-t(f(xy)-M)。 令g(u)=f(u)(u∈V(G)),g(uv)=M-f(uv)(uv∈E(G))。对于图G的每一条边xy∈E(G),有g(u)+g(v)=s′-tg(uv)。即(s,-t)∈P(G),所以g是图G的一个(s′,t)-魔幻全标号。 (2)设f为图G的超级强(s,t)-魔幻全标号,不失一般性,设:f(xi)=t+i(i∈[1,s]);f(yi)=j(j∈[1,t])。从而f(E(G))=[1+p,2p-1]。注意到 φ(yi)=2p-1-2f(yi)=2p-1-2j; 注意到f(E(G))=[1+p,2p-1],即有φ(E(G))={1,3,…,2p-3},故φ是图G的一个奇优美标号。 (3)设G的一个标号函数为Q,满足: Q(u)=p+1-f(u)(u∈V(G)),g(uv)=2p+q+1-f(uv)(uv∈E(G))。由于Q(u)+Q(v)=2(p+1)-(f(u)+f(v)) 定理6若(s,-1)∈P(H),则一致(k,m)-串图G有(s′,-1)∈P(G),且s′=m(s-1)+1。 证明: 步骤1.设二部分图G1,G2,…,Gm是图H的m个拷贝。(pi,qi)-图Gi的顶点集二部划分为(Xi,Yi),其中Xi={xi,li|j∈[1,ω]},Yi={yi,l|l∈[1,h]},以及pi=ω+h(i∈[1,m])。xi,ω,yi,1∈V(Gi),对于k≥1,用一条边分别连接顶点xρ,ω∈V(Gi)与顶点yρ,1∈V(Gi+1)后所得到的图G是(k,m)-串图(ρ∈[1,k])。令图G的一个标号函数Q满足: Q(yi,1)=(h-1)(i-1)+i; Q(xi,ω)=(h+1)i+tm; Q(yi,l)=Q(yi,1)+l-1; Q(xi,j)=Q(xi,ω)-ω+j。 步骤2.设f为(p,q)-图H的超级强(s,t)-魔幻全标号,由于f是超级的,不失一般性,设f(xj)=h+j(j∈[1,ω]),f(yr)=r(r∈[1,h]);f(xjyr)=p+q+1-θ(θ∈[1,ω+h-1]);因此f(E(H))=[1+p,2p-1]。令Q(yi,r)=r+h(i-1),Q(xi,j)=mh+j+ω(i-1),φ(xi,jyi,r)=2m(h+ω)-θ-(i-1)p,因此 Q(xi,j)+Q(yi,r)+Q(xi,jyi,r) =mh+j+ω(i-1)+r+h(i-1)+2m(h+ω)-θ-(i-1)p =h+j+r+m(p+q+1)-mθ+(m-1)(h+θ) =f(xi)+f(yi)+mf(xiyi)+(m-1)(h+θ) =s-f(xiyi)+mf(xiyi)+(m-1)(h+θ) =s+(m-1)(f(xiyi)+h+θ) =s+(m-1)(p+q+1-θ+h+θ) =s+(m-1)(p+q+ω+1-1) =s+(m-1)(s-1)=m(s-1)+1 令s′=m(s-1)+1,则有 Q(xi,j)+Q(yi,r)=s′-Q(xi,jyi,r)。 由定义1,3,有(s′,-1)∈P(G),如图1所示。 图1 1-维魔幻标号串图G的4个分解图((189,-1)-边魔幻全标号)Fig.1 Four decomposition graphs ((189,-1)-edge magic total labelling) of a 1D magical labling string graph G [1]GALLIAN J A.A dynamic survey of graph labelling[J].The Electronic Journal of Combinatorics,2010(17):6-189. [2]ALEXANDER Rosa.On Certain Valuations of the Vertices of a Graph[M].New York:Gordon and Breach,1966:349-355. [3]ANTON Kotzig,ALEXANDER Rosa.Magic valuations of finite graphs[J].Canada Math.Bull,1970,13(4):451-461. [4]KATHIRESAN K M.Two classes of graceful graphs[J].Ars Combinatoria,2000,55(4):129-132. [6]YAO Bing,ZHANG Zhongfu,YAO Ming,et al.A new type of magical coloring[J].Advances in Mathmatics,2008,37(5):571-583. [7]Albert William.Non super edge magic total labelling[C]//Joe Ryan.The Proceeding of The 4th International Workshop on Graph Labeling.Harbin,China:Harbin Engineering University and University of Ballarat,Australia,2008:44-48. [8]YAO Ming,YAO Bing,XIE Jianming.Some results on the k-magical labelling of graphs[J].Journal of Gansu Sciences,2010,22(1):1-6. [9]BONDY J A,MURTY U S R.Graph Theory with Application[M].Axler S,Ribet K A,New York:MaCmillan,1976:1-629. [10] YAO Bing,CHENG Xiangen,YAO Ming,et al.On(k,λ)-magically total labeling of graphs[J].Journal of Combinatorial Mathematics and Combinatorial Computing,2013(87):237-253. [11] LIU Xinsheng,LIU Yuanyuan,YAO Bing.Odd-gracefulness of dragon graphs[J].Journal of Lanzhou University of Technology,2013,39(3):135-139. [12] GALLIAN J A.A dynamic survey of graph labelling[J].The Electronic Journal of Combinatorics,2009(14):6-189. 责任编辑:张新宝 1-Dimension Magical Lablings of String Graphs YAO Ming1,YAO Bing2,ZHAO Zhengxue1 (1.Department of Information Processing and Control Engineering,Lanzhou Petrochemical college of Vocational Technology,Lanzhou 730060,Gansu,China;2.College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China) If there are integer paires such that a bijection of a connected graph from to satisfies for each edge,then is called a magically labeling.Furthermore,if there is minimum integer such that an abitrary-magically labeling satisfies,is called a one-dimension magically labeling.Hence,we defined the space of the magic total labellings and vector,and got 1-dimension magically labeling of the string graphs,and make use of methods of a vector algebra to research string graphs.The connections between one-dimension magically labeling and several known labelings (such as odd-graceful,dual lablings) are given.We presented a method to construct some large-scale graphs with the magic total lablings. dimension magically total labllings;magic total lablings;dual lablings;magical total labellings space;vector space 2016-01-06 国家自然科学基金资助项目(编号:61163054);甘肃省高等学校研究生导师科研项目(编号:1216-01);甘肃省财政厅专项资金(编号:2014-63) 姚明(1962-),男,副教授,主要从事图的着色和标号及计算优化。E-mail:yybm918@163.com 10.3969/j.issn.1673-064X.2016.03.020 O157.5 1673-064X(2016)03-0122-05 A


2 证明及主要结果
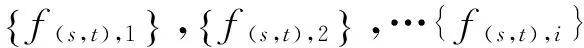
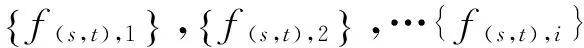
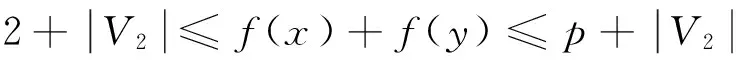

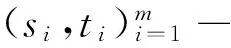
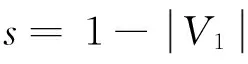
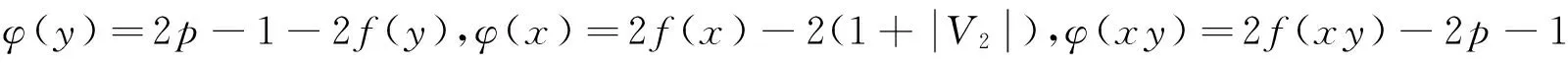
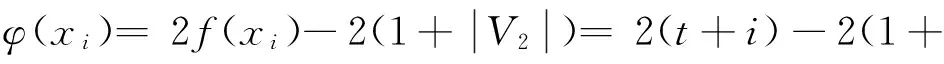
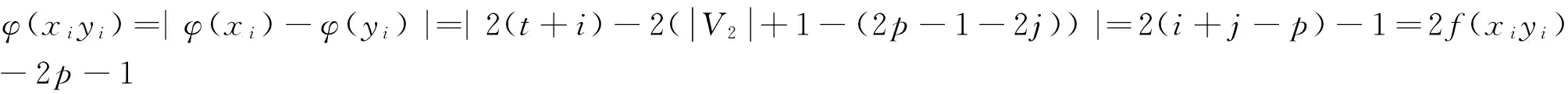
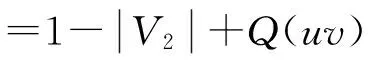
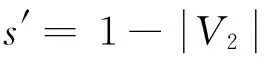
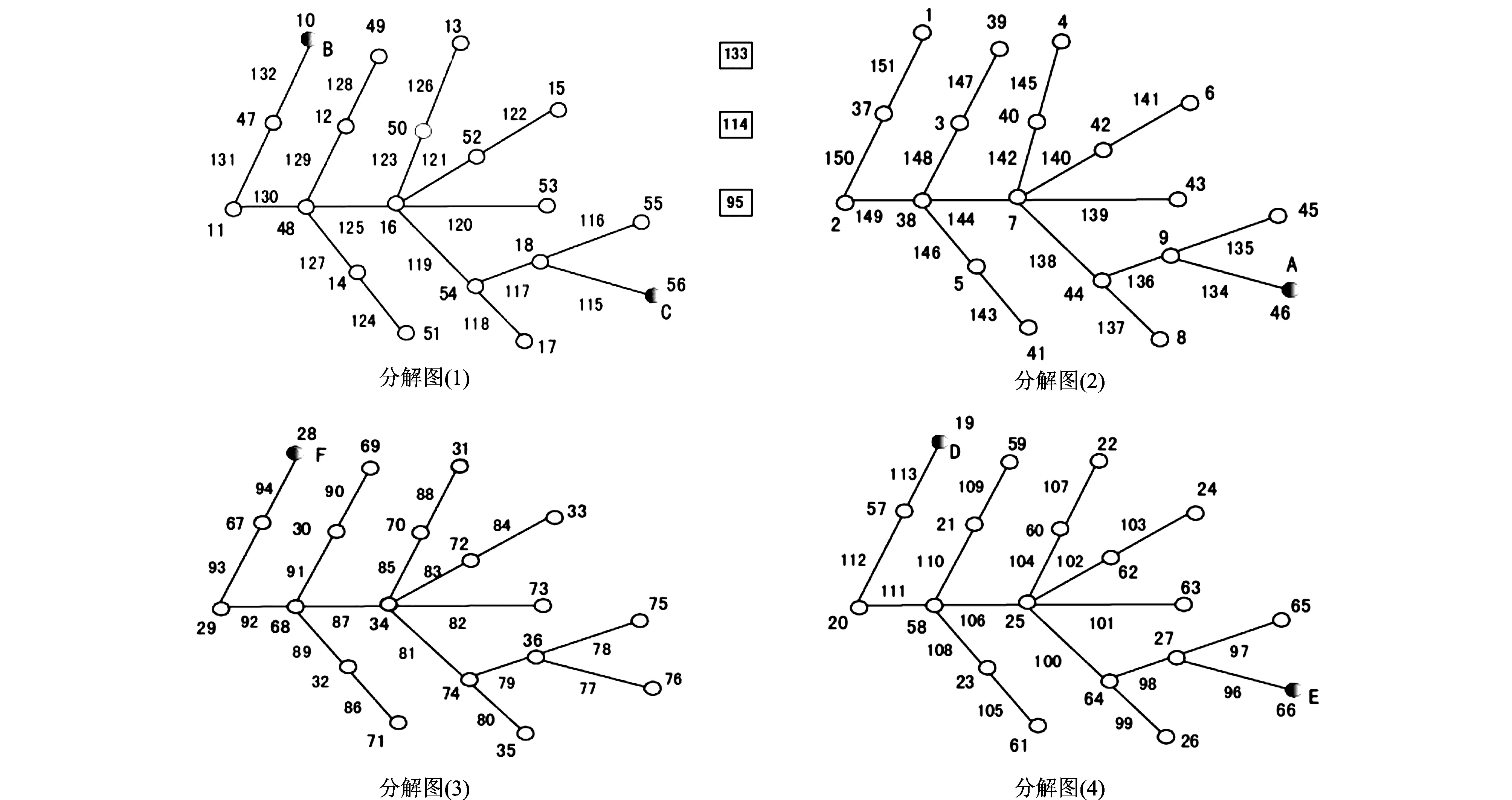
3 结 语