导弹结构热防护一体化设计与优化*

徐世南，吴催生

(中国空空导弹研究院， 河南 洛阳 471000)

导弹超高速飞行时，面临严酷的气动热力环境，给弹体结构带来重大考验[1-2]。随着新材料、新科技的不断发展，结构热防护一体化技术为导弹在超高速飞行时应对严酷环境提供了新的发展思路[3]。结构热防护一体化技术是热防护系统在完成防隔热功能的前提下，可同时承受其他飞行载荷，从而实现承载/防热一体化的技术[4]。

结构热防护一体化技术已经在各类高超声速飞行器中得到应用。Bapanapalli等[5]提出了波纹夹芯承载/防热一体化结构，该结构由上、下壁板和中间层的腹板构成，腹板空隙处填充隔热材料，以此实现高超声速飞行器的热防护。由于在隔热层较薄时腹板会出现热短路效应，导致热防护失效，为解决此问题，Darynabeigi等[6]设计了镂空结构的腹板。王琪等[7]对波纹夹芯承载/防热一体化结构进行了热力耦合分析，证明了此结构在高超声速飞行器中应用的可行性。除波纹夹芯结构外，蜂窝夹芯结构由于其比强度高，成为研究热点。吴大方等[8]对此结构进行了热冲击试验，发现它在高温环境下具有很强的抗变形能力。许磊[9]对蜂窝夹芯结构工艺进行了研究，实现了其在导弹天线罩上的研制。赵剑等[10]对蜂窝夹芯结构的传热特性进行了实验。此外，仿生学促进了许多新型承载/防热一体化结构的发展，如莲藕结构[11]、甲壳虫结构[12]等，均具有很好的承载与防热能力，但制造工艺较为复杂。为了改进一体化结构的性能，需要对其进行优化设计。Zhao等[13]采用模拟退火方法实现了波纹夹芯一体化结构的轻质化。Xie等[14]采用全局收敛移动渐近线法对波纹夹芯一体化结构进行了拓扑优化，优化方案中一体化结构比初始方案中减重37%。张志理等[15]采用遗传算法改善了波纹夹芯板的防护性能。刘伟先等[16]采用全局响应面法，以结构重量为目标函数，实现了蜂窝结构的减重优化。

目前，关于高超声速飞行器结构热防护一体化的研究，主要在壁厚厘米量级以上的飞行器中展开，而在毫米量级的飞行器上实现应用仍是难点。导弹壁厚一般在3 mm左右，将现有一体化结构应用于导弹，由于隔热层厚度降低，热防护性能变差，腹板的热短路效应加剧，会造成热防护失效，腹板镂空设计方法也不再适用，承载/防热一体化在导弹中的应用困难加大，需要对其进行设计与研究。在各类形式的一体化结构中，波纹夹芯结构制造工艺较为简单，更具应用优势[17]。本文基于波纹夹芯结构，对导弹进行结构热防护一体化设计；并建立其热力耦合仿真模型，验证其应用的可行性；进而分析此结构的防热特性，并以热防护效率最高和结构质量最小为优化目标，进行多目标优化设计。

1 结构热防护一体化设计与仿真建模

1.1 一体化设计

图1 波纹夹芯结构Fig.1 Corrugated core structure

波纹夹芯结构如图1所示。将此结构应用于导弹舱体，如图2所示。外壁为导弹外表面，承受力/热载荷，通常采用高温合金材料，以抵抗高温；中间部分为隔热层，由腹板和轻质隔热材料组成，腹板用来承载，轻质隔热材料填充在隔热层的空隙中，不负责承载，但可以减缓热量向内部的传递；内壁为导弹内表面结构，可采用较高比热容的金属材料，吸收一定热量从而避免导弹内部结构温度过高。将腹板和连接环相连接，不仅可以增强承载能力，而且结构壁厚大，热容高，可使此区域内表面温度有所下降，降低腹板区域的热短路效应。本设计的隔热层填充材料采用SY 1000[18]，其余结构部分均采用钛合金材料，具体材料参数见表1与表2。由此，保证舱体中间区域满足热防护目标，即可实现结构热防护一体化。

(a) 导弹舱体局部(a) Part of missile cabin

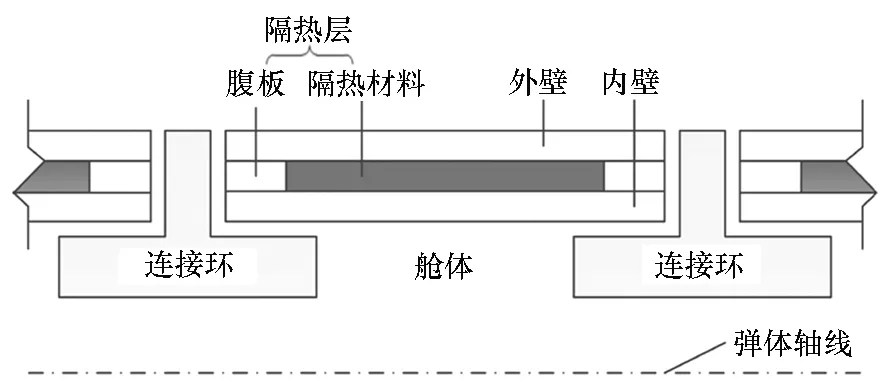
(b) 结构热防护一体化示意(b) Structure-thermal integrated protection图2 一体化结构设计Fig.2 Integrated structure design

表1 SY1000材料参数
Tab.1 SY1000 material parameters

密度/(kg/m3)热膨胀系数/℃-1热传导系数/(W·m-1·℃-1)比热容/(J·kg-1·℃-1)2002.45·10-6～3.09·10-60.016～0.064725～1100

表2 钛合金材料参数Tab.2 Titanium alloy material parameters

1.2 热-结构耦合模型

由于温度场与应力场相互作用的非线性程度有限，故可用间接法进行热-结构耦合仿真计算。基于文献[7]的方法，建立如图3所示的仿真分析流程。在进行结构热应力分析时，首先对结构进行瞬态温度历程计算，再选取某时刻的温度值作为载荷(一般可选温度最大值时刻)，最后进行结构应力应变分析。

结构热应力分析方程为：

(1)

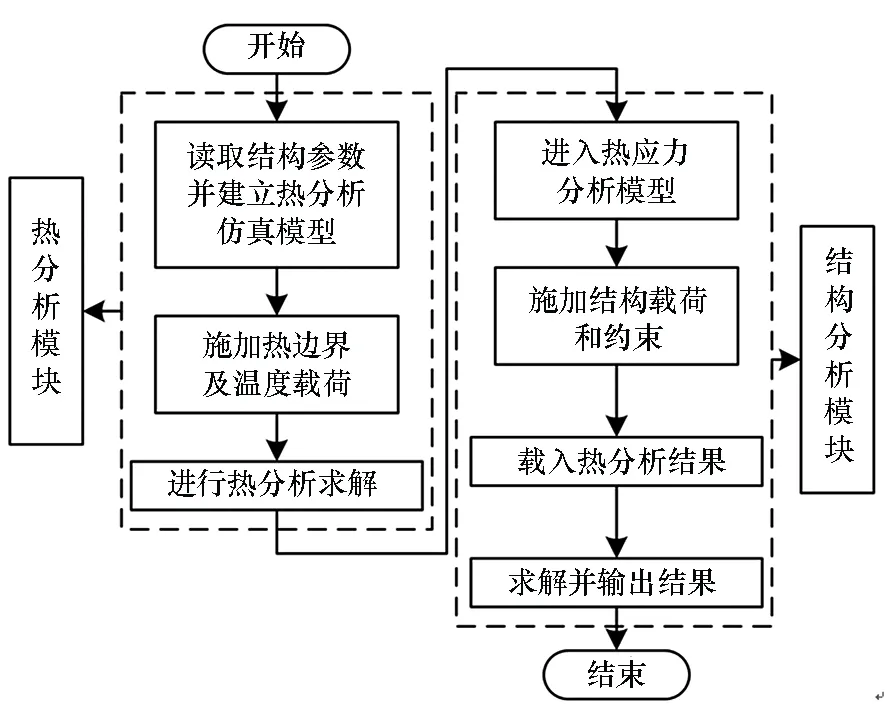
图3 热-结构耦合分析方法流程图Fig.3 Analysis flow chart of thermo-mechanical coupling

2 结构承载与防热性能分析

2.1 结构热-结构耦合分析

导弹高速飞行时，气动热与气动力载荷共同作用于弹体。以某型导弹的试验载荷为例，假设热防护目标为300 ℃，导弹舱体尺寸参数如图4所示；气动热载荷转化为温度载荷，如图5所示，施加在结构外壁，假设仿真模型无辐射，结构内壁底部绝热，将得到一个较为保守的仿真结果；将气动力载荷等效处理为1000 N·m的弯矩载荷；结构分析时根据圣维南原理，舱体结构模型两侧轴向均伸长合适长度，然后施加边界条件和结构载荷，其中一端采用固定边界条件，另一端施加弯矩载荷。

热-结构仿真计算时，对网格进行了收敛性检验，如表3所示。综合计算精度与效率，网格尺度取0.1 mm。

图4 舱体模型Fig.4 Cabin model

图5 温度载荷Fig.5 Temperature load

表3网格收敛性检验
Tab.3 Grid convergence test

编号网格尺度/mm距离舱体端部16mm温度/℃结构最大von-Mises应力/MPa1130137420.530039230.130039540.0530039650.01300396

热-结构耦合分析的温度结果如图6所示，温度呈轴对称分布，并且由端部高温区向中部低温区逐渐过渡。距离舱体端部16 mm区间内，内表面温度超过热防护目标(>300 ℃)，但此位置与连接环连接，可采取进一步热防护，且与连接环连接后(如图7所示)，此区域总厚度增加，热容增大，舱体内表面实际温度会有所降低。上述区间以外的内表面温度满足热防护目标，不再需要额外热防护。

图6 温度分布Fig.6 Temperature distribution

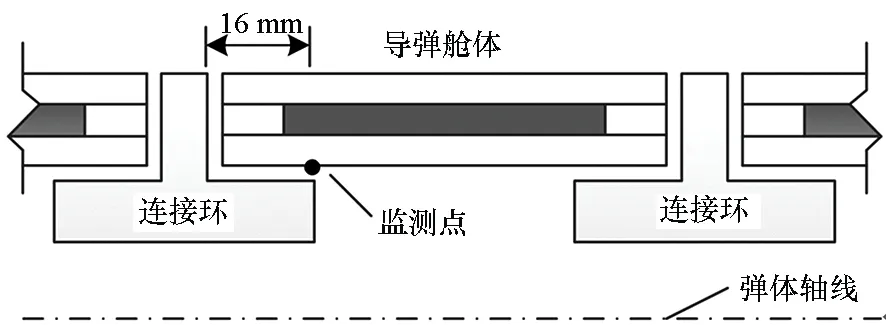
图7 舱体结构设计Fig.7 Structural design of cabin

热-结构耦合分析的应力结果如图8所示，证明该结构具有较好的承载能力。舱体中部应力较强，结构易发生破坏，属于应力薄弱区域。

图8 应力云图Fig.8 Stress distribution

2.2 防热特性分析

热防护效率定义：

η=(T0-Tin)/T0×100%

(2)

式中，T0为测点外壁温度，Tin为测点内壁温度。

对图7中监测点位置进行分析，研究其在40 s温度最高时刻的热防护特性。舱体半径和长度对热防护效率的影响如图9所示，其中舱体长度通过改变隔热层填充区域长度实现。由图可知，舱体半径和舱体长度对热防护效率影响很小，说明此设计方案可推广到其他型号导弹。

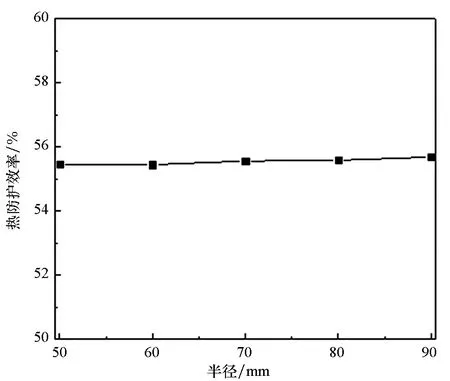
(a) 舱体半径(a) Radius of missile cabin

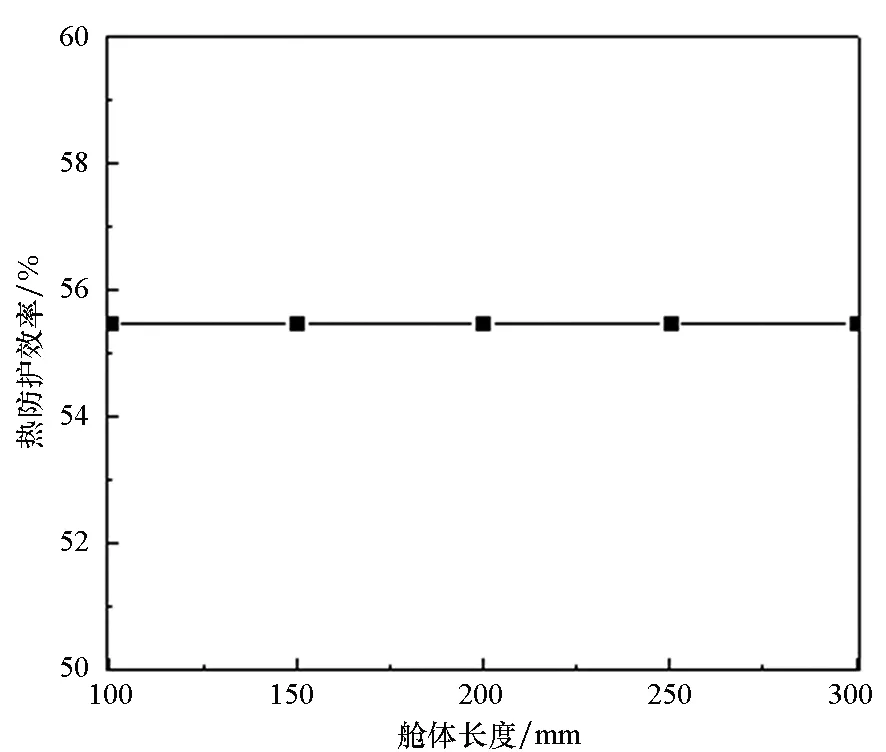
(b) 舱体长度(b) Length of missile cabin图9 热防护效率Fig.9 Thermal protection efficiency

在分别改变所关心参数尺寸，其余尺寸不变的情况下，研究结构内、外壁和隔热层厚度对热防护效率的影响，结果如图10所示。外壁厚度对结构热防护效率的影响较小，增加隔热层与内壁厚度有利于提高结构的热防护效率。增加隔热层厚度，结构隔热能力增强；增加内壁厚度，结构热容量增加，利于结构吸收更多热量。

图10 热防护效率Fig.10 Thermal protection efficiency

3 结构多目标优化设计

增加隔热层与内壁厚度有助于提高结构热防护效率，但受舱体壁厚尺寸限制，隔热层与内壁厚度增幅有限，且外壁厚度会因此降低，结构承载能力会受到影响。在实际应用中，不仅仅需要保证结构热防护效率，也需要实现结构轻质化，否则会因为导弹重量过重而影响飞行品质，因此需要进行结构多目标优化设计。

3.1 数学模型

进行导弹结构热防护一体化优化时，结合图4、图7建立初始设计模型，需要考虑以下几点因素：

1)弹体壁厚为3 mm；

2)结构需要具有较好的承载能力，在力-热联合载荷下，优化后结构应力小于材料极限强度；

3)考虑实际加工精度，将壁厚尺寸限定为小数点后一位。

以结构热防护效率最高和质量最小作为优化设计目标，为便于求解，定义目标函数如下：

(3)

式中，η(x1,x2)为结构热防护效率，m(x1,x2)为结构质量，x1为结构隔热层厚度，x2为结构内壁厚度，σ(x1,x2)为结构最大应力。

导弹一体化热防护结构的优化数学模型为：

(4)

3.2 优化方案

基于文献[19]的第二代非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ)进行优化分析，遗传运算采用精英保留策略，交叉与变异运算采用自适应策略，其中自适应率为[20]：

(5)

(6)

式中Pc1、Pc2、Pm1、Pm2为常数，Pc、Pm为自适应交叉和变异概率，F为待运算个体自适应值，Fmax和Favg分别为每代种群最大个体适应度值和平均适应度值。Pc1、Pc2、Pm1、Pm2可分别取0.9、0.6、0.1、0.001[20]。

优化流程如图11所示：首先，随机产生种群规模为N的初始父代种群，非支配排序后通过遗传运算得到种群规模为N的第一代子代种群；其次，从第二代开始，将父代种群与子代种群合并为种群规模为2N的临时种群，通过快速非支配排序和拥挤度计算，并根据非支配关系和个体拥挤度选取合适的个体组成种群规模为N的新父代种群；最后，通过遗传运算产生新子代种群；依此类推，直到满足程序终止条件。

图11 优化流程Fig.11 Optimization flow

3.3 优化结果分析

以目标函数值为适应度值，通过热-结构耦合有限元分析进行适应度值计算，初始种群规模取15，遗传运算终止条件为迭代数达到30[21]。

表4给出了三个Pareto非劣解，各结果的热防护效率与结构质量，相比于初始设计模型均得到优化。结果1的热防护效率较好，但是结构质量大，结果2与结果3的结构质量得到减轻，热防护效率却有所降低。所以在无其他决策条件的情况下，无法确定哪个是最优设计方案，这体现了多目标优化的特点。以结果1为例，其温度与应力云图如图12所示，结构在实现防热的同时，承载能力需求也得到满足，应力薄弱区域在舱体外壁。当需要进一步提升结构承载能力时，可根据优化结果对应力薄弱区域的结构进行加强。

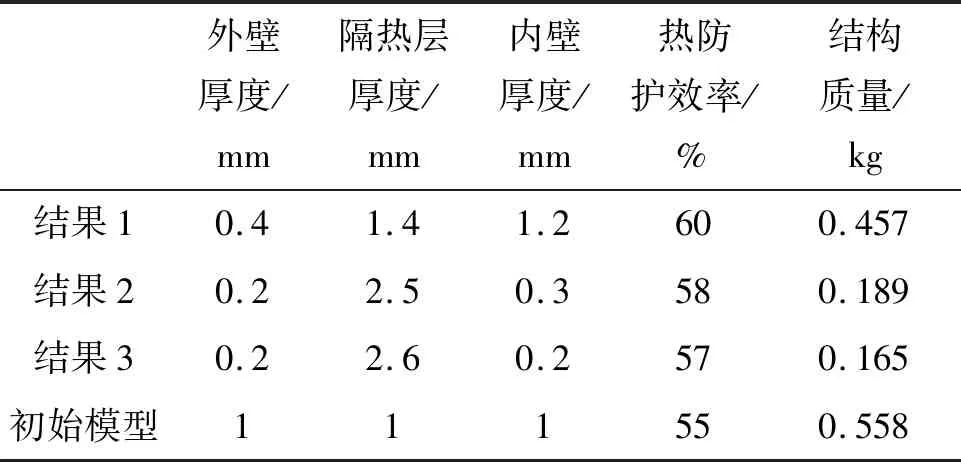
表4 Pareto非劣解Tab.4 Pareto non-inferior results

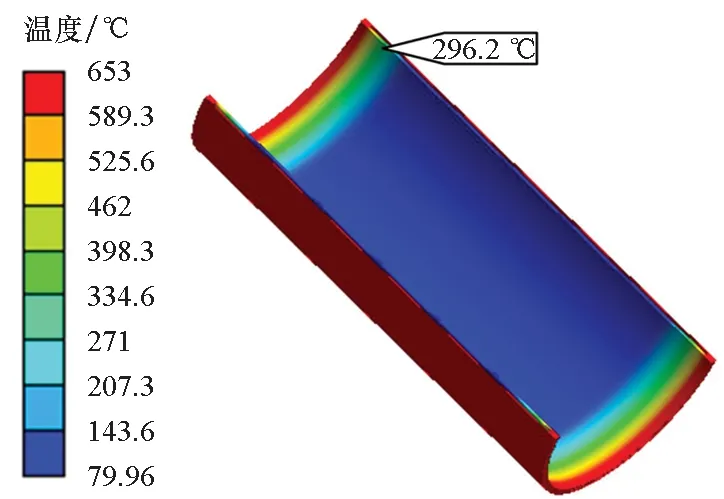
(a) 温度云图(a) Temperature distribution

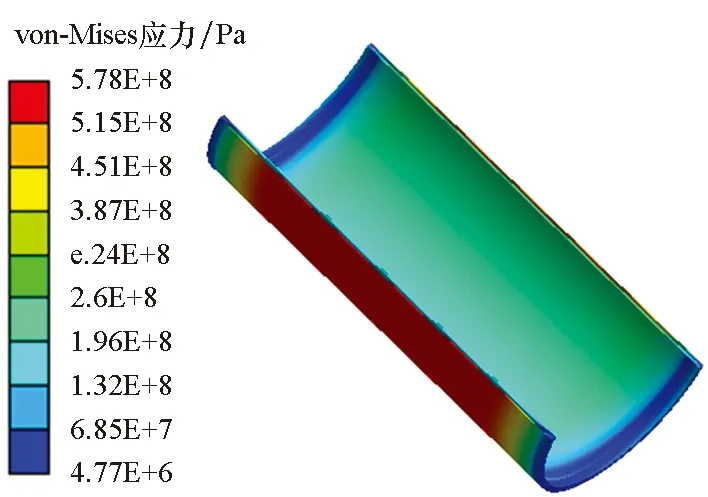
(b) 应力云图(b) Stress distribution图12 结果1云图Fig.12 Distribution of result 1

优化的Pareto最优化前沿如图13所示。优化结果与枚举法拟合曲线相吻合，验证了优化方法的有效性。Pareto最优化前沿两端体现了最高热防护效率设计与最低重量设计，应用中一般会采用权衡设计，选择Pareto最优化前沿中的某个方案。Pareto最优化前沿体现出结构热防护效率与质量相互制约，在优化设计时需要综合考虑结构热防护效率和结构质量这两个设计因素。

图13 Pareto最优化前沿Fig.13 Pareto front results

4 结论

1)基于波纹夹芯结构，导弹舱体两端与连接环连接共同承载，舱体内、外壁填充隔热材料，实现了结构承载与热防护一体化，为结构热防护一体化在小壁厚飞行器的应用提供了工程指导。

2)对一体化结构进行热防护特性分析发现，增加隔热层与内壁厚度可提高一体化结构热防护效率。

3)采用NSGA-Ⅱ优化算法，并引入自适应策略，进行导弹结构热防护一体优化设计，得到Pareto最优化前沿，提高了热防护效率，减轻了结构质量。研究表明，提高结构热防护效率会造成结构质量增加，这两个因素相互制约，设计时需要综合考虑。