多重优化的分布式无线覆盖探测算法*
王红军,向庭立,潘继飞
(国防科技大学 电子对抗学院, 安徽 合肥 230037)
随着通信技术的飞速发展和频谱资源的日益贫乏,为解决频谱冲突等一系列问题,无线通信网络信号覆盖范围高精度探测已逐步成为当前研究热点和前沿技术之一,世界各国都在军民通信领域着力研究如何显著提高无线通信网络的覆盖效能、传输的稳定性和安全性,以及如何降低传输的时延和功耗[1-2]。无线覆盖性能是无线通信网络一项重要指标,目前无线通信网络覆盖探测中较为成熟和广泛的方法是利用汽车加载测试终端和扫频仪等工具进行路测[3-4],但这种传统路测方法耗时耗力,且在路况较差尤其是野外会因难以到达环境下而无法进行。因此,有必要研究一种可高精度、全方位、全过程和全天候实现无线通信网络覆盖探测的技术路线。鉴于此,本文提出了基于无线传感器网络来实现对无线通信网络覆盖探测的研究方案。该方案通过预先部署的传感器节点形成分布式探测网络对接收信号强度(Received Signal Strength Indication, RSSI)进行采集,然后融合所有探测节点采集的数据生成目标区域内无线通信网络的有效覆盖范围,实现快速不间断的自动化感知[5]。其中探测节点可以通过无人机搭载等手段投放到待测区域,特别是可以投放到传统路测难以到达的区域中。
由于分布式探测节点所感知到的数据仅为该节点位置处的接收信号强度值,而最终要得到的是整个区域中无线通信网络的覆盖范围,因此,需要对传感器节点无法感知的探测盲区进行估计。目前主要有两种RSSI值估计方法:信号传播模型估计法和插值估计法[6]。其中,信号传播模型估计法基于RSSI值的分布趋势选取恰当的损耗模型来进行估计[7],复杂度较低,但现有模型通常无法与目标区域复杂多变的地理环境精确匹配,导致算法的估计精度较低。而基于邻域范围探测节点特征属性的插值估计法则相对可行且精度较高[8]。常用的插值估计法有:反距离加权插值法、牛顿插值法和Kriging插值法等。文献[9]采用牛顿插值法代替线性插值法对RSSI值进行估计,提高了插值精度,但是多项式插值函数的引入导致计算复杂度增加。文献[10]采用的反距离加权插值法在插值点较为分散的情况下精度较高,但是只考虑了节点间的位置关系,空间相关性较差。文献[11]基于传感器节点接收RSSI值的空间相关性,采用Kriging插值法实现了对探测盲区RSSI值的估计。然而Kriging插值法具有的平滑效应往往会掩盖空间数据变化剧烈区域的重要信息,导致这一区域插值表达不准确[12]。
近年来,时序分析、随机模拟、人工智能等诸多方法被用以克服Kriging法的缺陷。其中,人工神经网络在多属性数据分类和模式识别方面具有较强的能力,目前被广泛用于信号处理等众多领域中[13]。文献[14]成功将神经网络应用到基于RSSI值估计的定位问题之中。文献[15]研究发现Kriging插值法能够较好地反映目标区域的空间分布特征,但神经网络插值法的精度更高。文献[16]结合Kriging与神经网络插值法,再现了区域化变量的空间特征,一定程度上提高了插值精度。但由于神经网络存在局部收敛的缺陷,插值精度还有待提高。针对该问题,文献[17]利用粒子群优化(Particle Swarm Optimization, PSO)算法对BP(back propagation)神经网络的初始权重系数进行优化,得到了收敛性更好且精度更高的PSO-BP模型。
针对以上算法应用在无线通信网络覆盖探测中的不足,本文提出一种多重优化插值算法。该算法利用变异函数重新构造BP神经网络的目标函数,并利用改进粒子群算法对其初始权重系数进行了优化,形成一种改进粒子群神经Kriging插值算法(MPSO-BP-Kriging, MPBK),克服了Kriging插值法过于平滑的空间表达以及神经网络插值法局部收敛等缺点,提高了无线通信网络覆盖探测的可信度和精度。
1 算法描述
1.1 Kriging插值法原理
Kriging插值法是一种研究空间变异和插值的线性无偏估计方法,普遍用于地质测量领域的格网化统计[18-19]。本文利用领域范围内传感器节点的特征属性(即采集到的RSSI值)实现对插值点RSSI值的估计。
设插值点RSSI值为Z(x0),其邻域范围内m个传感器节点接收的RSSI值为Z(xi)(i=1,2,…,m),则Kriging插值法的估计公式为:
(1)

(2)
要使Z*(x0)为Z(x0)的无偏估计,即要求x0估计方差最小:
Dmin(x0)=D(Z(x0)-Z*(x0))
=E([Z(x0)-Z*(x0)]2)
(3)
引入Lagrange乘数μ求条件极值,可表示如下:
(4)
通过推导可得Kriging线性方程组为:
(5)
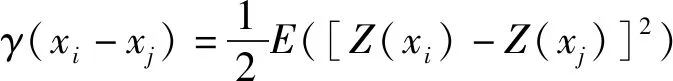
变异函数的提出是为了描述区域化变量的空间分布特征,是Kriging插值法的核心。通过已知点的特征属性随空间位置变化的规律,变异函数可以推断出未知点的属性值,其值可以通过式(6)进行计算:
(6)
式中,h为区域内一对采样点的间隔距离,N(h)为所有采样点对中间隔距离为h的点对数。根据式(6)对不同间隔距离的变异函数值进行求解即可拟合γ(h),然后得出邻域范围内插值点与采样点特征属性间的变异函数值,代入线性方程组(5)即可求得Lagrange乘数μ和权重λi。
现有研究往往利用经典变异函数模型对变异函数曲线进行最小二乘法拟合[11]。基于此,Kriging插值法所表达的空间分布是平滑的。
1.2 BP神经网络插值原理
BP神经网络是基于误差反向传播算法的多层前馈神经网络。大量研究已经证明,隐层中具有足够节点的三层BP神经网络具有模拟任何复杂非线性映射的能力[20]。
设有P个样本,每个样本有N个输入分量和M个输出分量用于网络训练。利用节点功能函数式(7)计算节点输出:
(7)
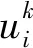
利用目标函数F计算输出误差:
(8)
式中,oj,p表示网络输出,yj,p表示期望输出。
当F小于设定误差ε,训练结束。利用训练好的网络模型即可对未知点特征属性进行插值估计。然而,神经网络插值法虽然估计结果精度虽然较高,但却无法保证再现空间相关结构。
2 分布式无线覆盖探测算法
本文提出的分布式无线覆盖探测算法利用多重优化插值算法实现了对目标区域的无线通信网络信号覆盖探测。基于无线传感器的分布式探测网络可以实时地采集数据,达到随时随地进行探测的目的,能够较好地满足无线通信网络信号覆盖实时实地重复探测的需求。算法架构如图1所示。
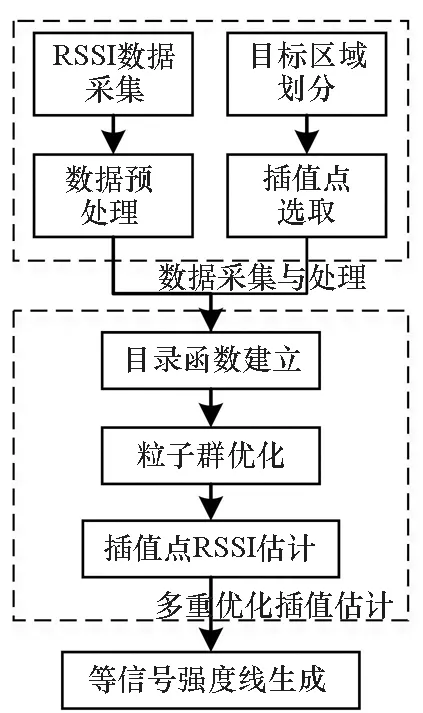
图1 无线通信网信号覆盖探测技术架构Fig.1 Wireless communication network signal coverage detection technology architecture
算法主要由三个模块组成:数据采集与处理、多重优化插值估计和等信号强度线生成。其中,数据采集与处理主要完成预处理工作;多重优化插值估计主要完成建立目标函数、粒子群优化和插值估计工作;等信号强度线生成则结合预先采集的RSSI数据和插值估计数据生成无线覆盖等信号强度线。
2.1 数据采集与处理
为确保数据准确性,首先多次重复独立采集RSSI数据,可知采集数据服从高斯分布[21]。利用高斯滤波可滤除样本中的小概率项,进而获取准确的RSSI数据。
因此,选取概率密度函数式(9)中f(x)≥0.6(经验值)区间内的数据,并求其均值作为所需的样本数据。
(9)
(10)
(11)
式中,RSSIm表示第m次采集数据,n表示采集次数,τ为均值,σ2为方差。
其次,利用处理得到的样本数据对目标区域进行划分和插值点选取。利用Delaunay网格划分法将目标区域划分为若干封闭三角形,以传感器节点所在位置处为三角网格顶点,每个网格即可选取一个插值点[22]。
2.2 多重优化插值算法
2.2.1 目标函数构造
前述提到Kriging插值法的空间相关性较好但表达过于平滑,神经网络插值法的精度较高但空间结构性较弱。为克服两种方法缺陷,构造目标函数如下:
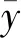
作为新的学习标准,该目标函数包含了变异函数和估计值的误差,能够有效改善神经网络的插值表达。
2.2.2 改进粒子群优化BP神经网络
BP神经网络的误差反向传播算法虽然倾向收敛于小型网络,但在训练复杂数据分布模式的条件下,它仍容易陷入局部最小值。粒子群算法具有易于实现、高效智能的特点[23],将神经网络目标函数引入粒子群适应度函数,即可对初始权值和阈值进行优化。然而,标准粒子群算法同样存在陷入局部最优的可能性。为提高算法有效性,需要对标准粒子群算法进行改进。
标准粒子群算法寻优过程中,粒子依据式(13)更新速度和位置:
(13)
其中:vid表示第i个粒子的第d个速度分量;xid表示第i个粒子的第d个位置分量;pid表示第i个粒子的最优位置分量;pqd表示所有粒子中的最优位置分量;c1和c2为学习因子,r1和r2为[0,1]区间内的随机数,ω为惯性因子。为平衡算法全局探测能力与局部开采能力,搜索过程中可对ω进行动态调整。文献[24]提出一种ω线性递减调整策略:
ω=ωmax-(ωmax-ωmin)t/Tf
(14)
式中,ωmax和ωmin分别表示惯性因子终止值和初始值,t表示当前迭代次数,Tf表示最终迭代次数。该策略在一定程度上提高了算法性能,但在初期迭代,ω过大可能导致粒子跳过最优位置,从而影响算法的搜索效率;后期迭代,ω则可能过小,导致算法精度下降。
针对该问题,本文利用一种随迭代次数逐步递减的波动因子β对惯性因子ω进行自适应改进,具体公式如下:
ω=ωmax-(ωmax-ωmin)t/Tf+β×randn
(15)
β=e(-t/Tf)/2
(16)
式中,randn为服从标准正态分布的随机数。初期迭代β较大的ω增强了算法的全局探测能力;后期迭代β较小的ω提高了算法的局部开采能力。一般情况下,ω取[0.4,0.9](详见文献[25])。
则改进粒子群算法优化BP算法步骤为:
1)粒子初始化。
2)适应度函数值计算。
3)个体及群体最优值计算。
4)更新粒子速度及位置。若优化过程中提前到达最大迭代次数,则算法停止并输出此时最优解,否则返回第2步。
5)将得到的最优权重系数赋予BP神经网络模型。
6)计算模型误差,若误差未达到目标值,则继续更新网络权值和阈值至误差条件满足。
2.2.3 多重优化插值算法流程
前述提到与普通Kriging插值法和BP神经网络插值法相比,本文提出的多重优化插值算法具有更高的精度,能够有效克服单独使用两种传统方法进行插值估计的缺点,算法的具体步骤如下:
1)利用样本数据计算γ(h)并选择合适的模型进行拟合;
2)确定网络参数,如学习因子和速率、目标误差ε以及最大迭代次数等;
3)根据不同传感器节点对的分离距离hk及对应γ(h),求取式(12)中的变异函数γ(hk);
4)利用PSO算法获取神经网络初始权重;
5)根据式(7)计算节点输出;
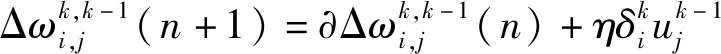
7)根据样本数据和网络输出的误差以及γ*(hk),由式(12)求F;
8)若F≤ε,此时的权重即为网络模型最后的权重,否则返回第4步;
9)选择其他样本验证网络模型的拟合效果,若满足条件,则进入下一步,否则返回第4步;
10)利用训练好的网络模型进行插值估计。
3 仿真实验分析
3.1 仿真环境构建
为验证所提分布式无线覆盖探测算法性能,以5 G通信测试网为例,选取400 m×400 m的某郊区作为实验的实际环境进行仿真实验。假设该地区存在4个5 G通信基站,通过ATOLL仿真得到基站信号覆盖情况如图2所示。通过随机部署的方法投放42个传感器节点于该地区。仿真实验过程中假设基站位置、个数以及信号覆盖情况未知以验证算法有效性。
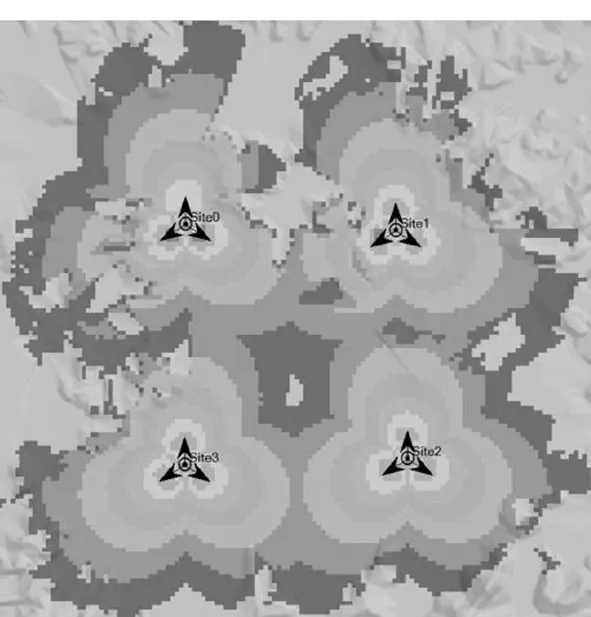
图2 仿真环境 Fig.2 Simulation environment
为了便于对比分析插值精度,随机选取其中34个传感器节点作采样点,余下8个节点作验证点。从预测模型对比分析、插值算法性能分析、等信号强度线生成等方面设计了多个仿真实验以验证所提算法性能。
3.2 预测模型性能分析
3.2.1 预测模型精度对比
为了验证插值估计结果精度,分别采用普通Kriging模型、BP模型、BK模型以及MPBK模型对插值点RSSI值进行预测,以第3.1节选择的34个采样点为样本,随机选取其中70%数据作训练集,其余30%作测试集,预测结果如图3所示。
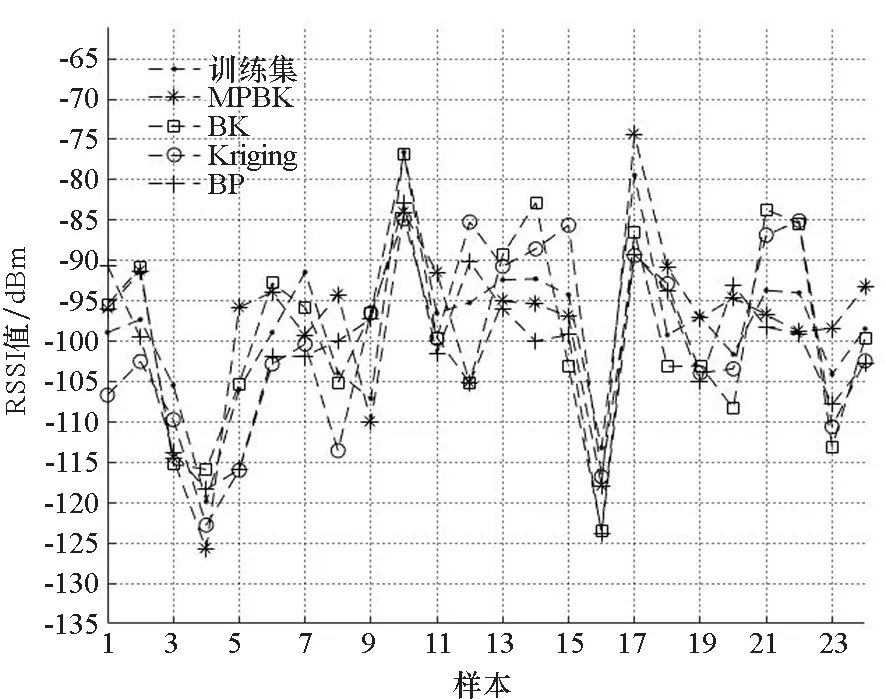
(a) 训练集预测结果(a) Training set prediction results
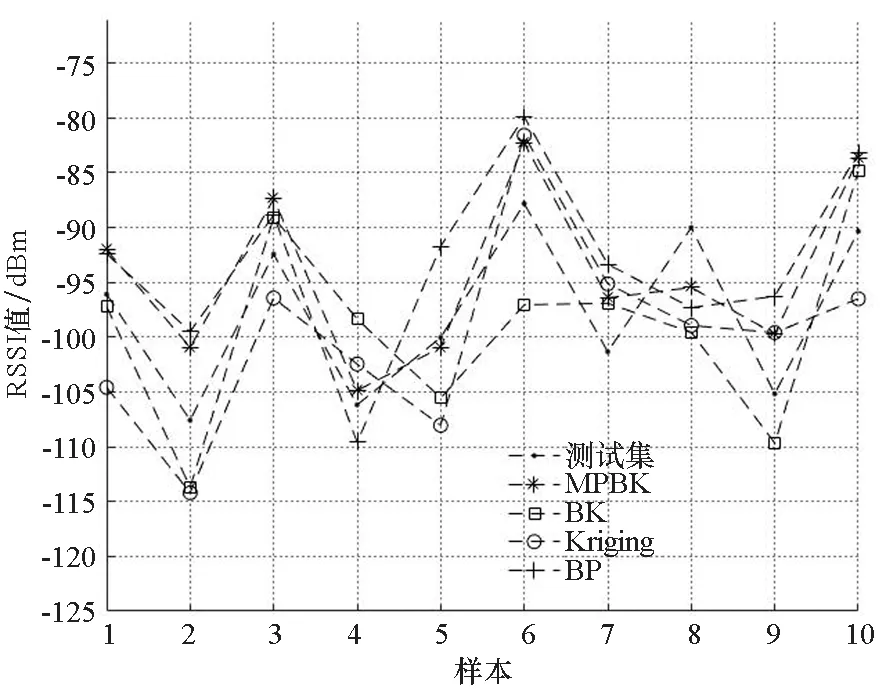
(b) 测试集预测结果(b) Test set prediction results图3 预测结果Fig.3 Prediction results
为了对比算法精度,分别计算训练集和测试集中各模型的均方根误差(Root Mean Squared Error, RMSE)。训练集中普通Kriging模型为6.967,BP模型为6.795,BK模型为6.732,MPBK模型为6.051;测试集中普通Kriging模型为6.903,BP模型为6.764,BK模型为6.291,MPBK模型为5.875。通过对比可知,MPBK模型均方根误差更低,精度更高。
为了更有效地衡量几种模型的预测精度,对34个传感器节点进行6000次随机独立抽取实验,并对平均均方根误差RMSE和平均决定系数R2进行计算,实验结果见表1。
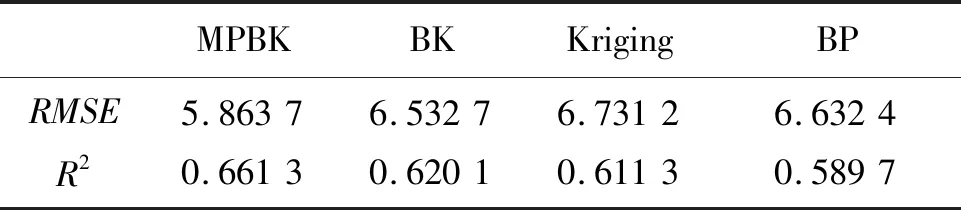
表1 模型预测性能对比Tab.1 Model prediction performance comparison
由表1可知,MPBK模型预测结果的平均RMSE低于其他模型,且具有更高的平均R2,因此其具有更高的预测精度。
3.2.2 算法适用性分析
首先对算法的鲁棒性进行分析。由于传感器节点部署在目标区域之后,可能出现能量消耗殆尽等各种情况,造成能够有效工作的传感器节点数量以及采集到的数据量减少,势必要求算法具有一定的鲁棒性。基于此,通过逐次增加失效传感器节点数量的方式进行鲁棒性实验,并计算各模型均方根误差RMSE,实验结果如图4所示。
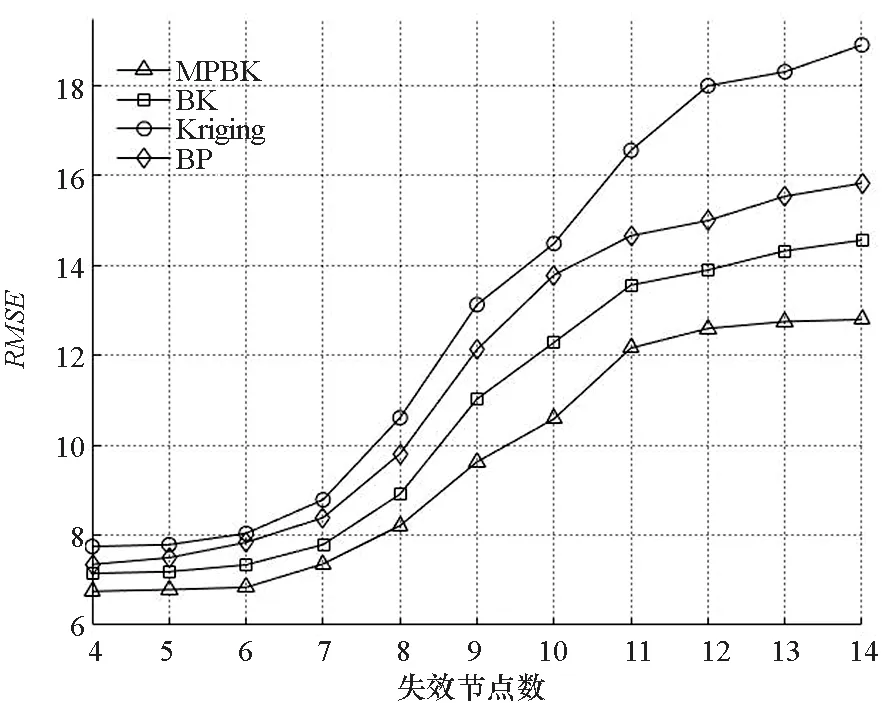
图4 失效节点数与RMSE关系Fig.4 Relationship between number of failed nodes and RMSE
通过图4可以看到,当失效节点个数小于7时,各模型RMSE变化均较为平稳,其中MPBK模型最低;当失效节点个数达到7时,各模型RMSE开始呈现上升趋势,其中普通Kriging模型增长趋势最快。经过对比分析可知,MPBK模型的预测结果更为稳定,鲁棒性优于其他模型。
其次对算法的复杂度进行分析。结合机器学习方法所采用的多重优化插值方法一定程度上增加了计算的时间复杂度,但在还原一定区域信号覆盖的真实情况时,由于更高的预测精度和更好的鲁棒性,通常只需要采集更少的传感器节点数据。而其他算法则可能需要多次采集以确保数据的准确性,一定程度上反而增加了计算的开销。
综上所述,MPBK模型具备精度高、鲁棒性好的优点。综合考虑模型预测精度、算法鲁棒性和复杂度等因素,当传感器节点数据处理能力较强时,可以采用MPBK模型进行预测。
3.3 插值算法性能分析
为了验证所提多重优化插值算法精度,以第3.1节选取的8个节点为验证点,分别利用4种模型对8个验证点进行插值估计预测,并与真实值进行对比,实验结果如图5所示。
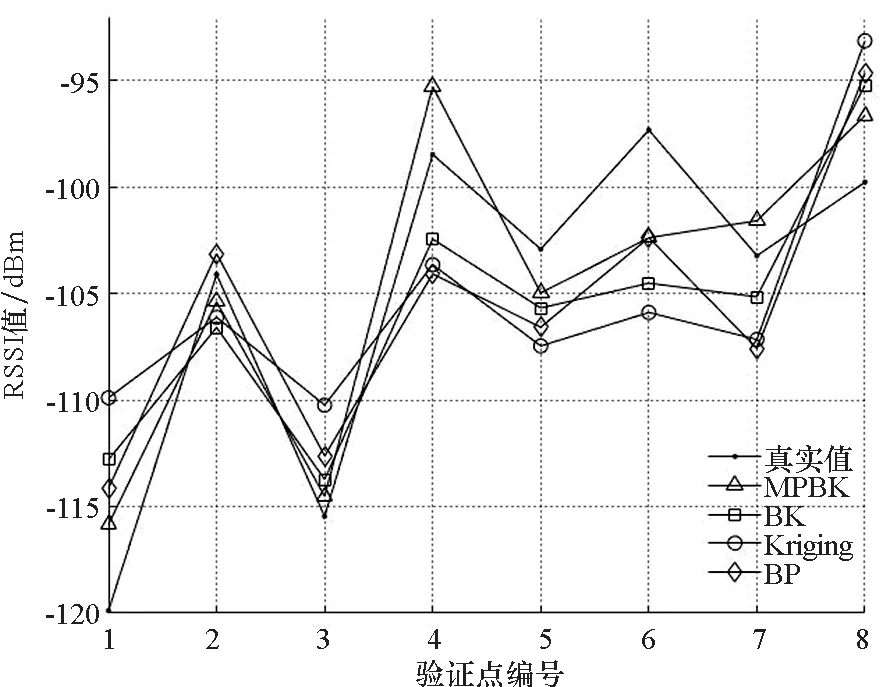
图5 插值算法对比Fig.5 Comparison of interpolation algorithms
分别计算4种模型的均方根误差,其中普通Kriging模型为7.014 1,BP模型为6.313 5,BK模型为5.355 7,MPBK模型为4.320 8。不难发现本文所提多重优化插值算法的均方根误差更小,精度更高,算法性能最好。
3.4 等信号强度线生成
分别利用前述4种算法进行插值估计,并结合传感器节点采集到的数据和插值估计得到的数据生成目标区域的等信号强度线,如图6所示。
为了验证所生成等信号强度线的精度和可信度,在目标区域中选择60个位置点进行6000次随机独立抽取实验,并分别计算以上4种算法在这些位置点处插值估计结果的平均RMSE。其中,普通Kriging模型的平均RMSE为17.317 4,BP模型为15.204 6,BK模型为13.637 1,MPBK模型为9.659 4。通过对比可知,本文所提多重优化插值算法具有更高的精度,生成的等信号强度线也更加接近目标区域无线通信网络信号的实际覆盖情况。

(a) 普通Kriging插值结果(a) Ordinary Kriging interpolation results

(b) BP插值结果(b) BP interpolation results

(c) BK插值结果(c) BK interpolation results

(d) MPBK插值结果(d) MPBK interpolation results图6 等信号强度线Fig.6 Equal signal strength line
4 结论
针对常规无线通信网络覆盖探测耗时耗力且易受环境和地形影响的局限性,本文提出了一种基于无线传感器网络的分布式无线覆盖探测算法,利用多重优化插值算法实现了对存在探测盲区的目标区域的等信号强度线生成,能够较为直观地反映目标区域无线通信网信号的覆盖状况,对衡量无线通信网的覆盖性能具有一定参考价值。通过仿真实验验证了所生成等信号强度线的有效性。当无线传感器节点在目标区域部署完毕,本文算法可以全天候全方位进行等信号强度线的生成,能够较好地满足运营商对无线通信网信号覆盖探测实时实地可重复等特殊要求,具有一定普适性。

