高精度CFD程序的内外子区域划分异构并行算法*

王 巍，徐传福，车永刚

(国防科技大学 计算机学院 量子信息研究所兼高性能计算国家重点实验室， 湖南 长沙 410073)

计算流体力学(Computational Fluid Dynamics, CFD)采用数值方法求解流体运动相关微分方程，从而揭示流动现象和规律，是涉及流体力学、数学和计算机科学等多个学科领域的交叉学科。20世纪60年代以来，随着高性能计算技术的发展，CFD也获得了迅速的发展，目前已被广泛应用于航空航天、航海、汽车制造、生物医疗、环境工程、核工业等众多领域。然而，在研究和设计中要使CFD手段达到高保真度水平将引入巨大的计算量，这对现代高性能计算平台的计算和存储能力等提出了极高的要求[1-2]。

另一方面，自2008年的P级计算机问世，超级计算机的发展向E级计算能力水平推进，以满足应用领域的迫切需求。这也使得一系列相关技术，如网络通信、存储结构等，都面临着新的挑战，然而最重要和最根本的是解决能耗问题[3]。为此，异构超级计算机的概念作为解决方案被提出来。概念上，异构超级计算机主要是指计算单元集成了处理器和所谓的加速器，或称协处理器。目前一种被广泛使用的加速器是通用图形处理器(GPGPU)，目前世界超级计算机排行榜(Top500)中最快的超级计算机——Summit就使用了27 648块NVIDIA Volta V100 GPU作为加速器。另一种重要的加速器是Intel Xeon Phi系列协处理器(MIC)，这是一种基于片上系统架构的众核加速器，在“天河二号”、Stamped等超级计算机中得到使用[4-5]。现今，异构系统正成为在能耗允许的范围内建造更大规模和更强计算能力的超级计算机的有力选择[6-7]。

然而，要使CFD应用在异构平台上获得良好的性能，将面临新的问题，如异构计算资源之间的数据传输开销、计算能力的差别，以及负载均衡等。针对异构超级计算机系统的特点，将CFD应用以合适的方式面向异构平台移植，是使CFD应用充分发挥异构超级计算机性能的关键技术，也是领域内的热点课题，已有大量相关研究工作。美国橡树岭国家实验室与CRAY、NVIDIA等[8]合作实现了燃烧模拟软件S3D的MPI/OpenMP混合并行，并基于OpenACC实现了其GPU并行计算，使用Fermi GPU相对于CPU的加速为1.2倍，在Titan超级计算机上的测试规模最大达8192节点。俄罗斯凯尔迪什应用数学研究所Gorobets等[9]基于MPI+OpenMP+OpenCL并行编程，实现了一个采用有限体积法求解可压缩Navier-Stoke方程的CFD软件的大规模并行，并在多核CPU、MIC、GPU等体系结构上进行了性能测试与对比，其大规模异构并行计算扩展到了320个GPU，相对于48个GPU的并行效率超过90%。西班牙加泰罗尼亚技术大学lvarez 等[10]基于MPI+OpenMP + OpenCL编程实现了HPC2框架，在此基础上实现了一个不均匀加热充气腔中的湍流流动算例的并行计算，在一个每结点含2块NVIDIA K80 GPU的集群上，从1个节点扩展到64节点时的并行效率达到94%。国内Cai等[11]在神威太湖之光超级计算机上，针对极大规模三维爆震波模拟中高阶WENO计算问题设计了高效的并行算法和优化技术，测试表明可扩展到998万核，获得23.1Pflops的性能。

对此，本文针对一个基于有限差分和4阶龙格-库塔(Runge-Kutta)方法显式时间推进的高阶精度CFD求解器——CNS，提出了一种Offload模式下的，对任务内外子区域划分的异构混合算法，从而提升程序在异构平台上的单节点性能。工作和贡献如下：

第一，对CNS求解器在Offload模式下的异构程序引入了一种新的内外子区域的任务划分策略。这种内外子区域的任务划分策略把CNS求解器已有的任务子块再次划分为内部区域和外环区域两个子区域，将程序在内部区域的计算放在加速器端来执行，外环区域的计算和MPI 通信放在CPU端执行。这种方式让加速器端的任务子块成为被外环区域包裹的彼此独立的内部区域块，这样使加速器的计算之间相互独立，没有数据关联；并且可以通过调整内部子区域和外部子区域的大小比例，来灵活地控制CPU端和加速器端的计算负载，获得良好的负载均衡。

第二，在内外子区域的任务划分策略基础上针对显式算法的特点进一步设计ghost网格点区域，并通过引入ghost区域提出了一种ghost网格点缩减计算模式，这种模式仅在一个时间推进步开始和结束的时候进行CPU和加速器之间的数据传输，而在4 阶Runge-Kutta法计算的内部则完全不进行CPU和加速器之间的数据通信。这极大地减少了Offload模式下异构程序异构计算资源之间的数据传输开销，并且使得CPU端的任务和加速器端的任务在一个时间推进循环内部，完全独立地各自分别进行，仅随着循环开始和结束同步，这样，在负载均衡的情况下，CPU端的计算和MPI通信，与加速器端的计算完全地重叠起来。给出了可以保证计算正确性的ghost网格点区域的宽度。

第三，基于OpenMP 4.5实现了该异构算法，并分析了负载均衡的条件，最后对程序在CPU+MIC结构的平台上进行了性能测试。测试表明，基于内外子区域划分的异构算法显著提升了CNS程序在异构平台上的性能，相较于已有的直接以网格子块为单位进行任务分配的异构并行算法，在本文测试的三种数据规模下，平均有5.9倍的性能提升。在单节点上，相对于不使用加速器时，基于内外子区域划分的异构算法在使用单块MIC卡和两块MIC卡时，分别获得了最大1.27倍和1.45倍的性能加速。

1 高精度CFD求解器CNS

CNS(compressible Navier Stokes)程序是一款用于求解空气动力学问题的高精度CFD求解器，是一款in-house代码。该程序提出的稳定有限差分格式，满足能量估计和分部求和规则[12]，求解全三维可压缩Navier-Stokes方程组。CNS在航空航天科研领域具有良好的应用背景，同时，程序包含复杂的计算。

1.1 CNS中的控制方程组

CNS求解的控制方程组包括方程(1)～(4)：

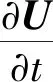
(1)

(2)

p=P(γ,ρ,e)

(3)

T=Temp(γ,Ma,ρ,p)

(4)

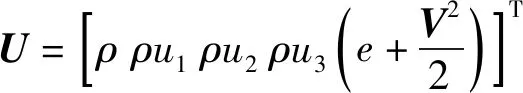
1.2 基本的数值方法和程序

CNS程序基于结构化网格求解控制方程组，网格点沿着xyz方向均匀分布，如图1，针对网格点i,j,k，图中用灰色表示，在计算某一个坐标方向的数值偏导数的时候，将使用前后各6个相邻的网格点的数值来构建差分形式(xyz方向分别为图1中绿色、蓝色、橙色)。同时，时间推进采用显式4阶Runge-Kutta方法，并且所有的计算矩阵都是稠密的。这些不仅带来巨大的数据量和计算量，也增加了MPI 通信开销和使用异构平台时异构计算资源之间的数据传输开销。

CNS程序的原始版本基于MPI的并行程序，它将一个正六面体空间计算区域均匀地分解成nprocsx×nprocsy×nprocsz个子块，采用笛卡尔进程通信拓扑，每一个进程承担一个子块的计算，每一个任务子块有相同数量的网格，这样负载是均衡的。初始版本的CNS程序本身具有良好的并行可扩展性。

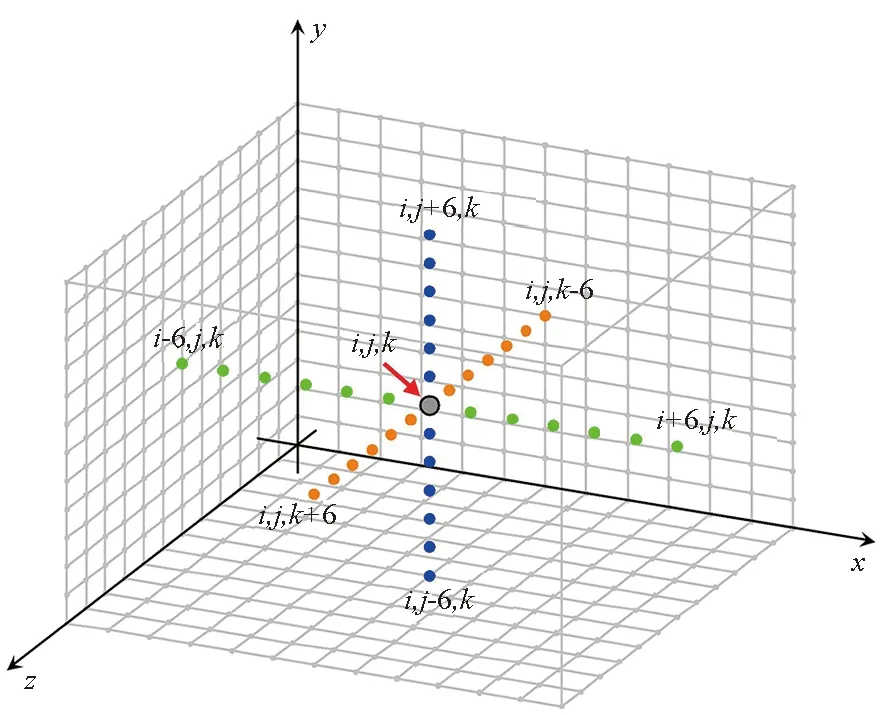
图1 CNS程序的网格和差分示意Fig.1 Finite difference stencil in CNS

CNS程序主循环的计算内核RK4包含了4阶Runge-Kutta法的4个计算阶段，如图2(a)所示。控制方程组所有项和结果的计算都在RK4函数中执行，其中包括两大主要计算模块：通量项的计算，即函数cacul_flux，如图2(a)中步骤③所示；Φ项的计算，即函数cacul_Φ，如图2(a)中步骤⑤所示。cacul_flux和cacul_Φ包括了CNS程序全部的差分操作，为了保障cacul_flux和cacul_Φ中的差分计算在边界附近可以顺利执行，程序通过MPI通信对子块外围的数据缓冲区进行了填充，如图2(a)步骤②和④所示。

2 Offload异构模式和已有的工作

Offload模式是以CPU为主，加速器为辅的一种异构执行模式。相对于加速器和CPU对等模式、加速器原生模式等来说，Offload模式更有利于异构平台计算资源的充分利用和CPU端与加速器端的负载均衡。所以，一般使用Offload模式来构建和执行异构程序。

由于CNS程序原始代码采用一个进程计算一个任务子块的模式，要将其重构成Offload模式的异构程序，最直接的做法是将一部分子块(进程)的计算迁移到加速器上去，将一部分子块的计算保留在CPU端进行，后面我们将在加速器上计算的子块称为Offload子块，在加速器上计算的子块对应的进程称为Offload进程。这样，加速器和CPU上的计算资源都得到了利用，并可以通过调整在加速器上计算的子块和在CPU上计算的子块的数量比例，调整CPU端和加速器端的负载。

(a) 原始MPI并行算法过程示意(a) Original algorithm procedure

(b) Direct-Offload算法过程示意(b) Direct-Offload algorithm procedure

(c) Subdomain-Offload算法过程示意(c) Subdomain-Offload algorithm procedure注：①还原基本未知量，边界条件加载；②MPI通信，填充基本未知量边界；③计算通量项F、G、H；④MPI通信，填充通量项边界；⑤计算Φ项：cacul_Φ；⑥更新U数组；⑦收敛检验、文件输出等；⑧结束工作图2 三种算法的执行过程Fig.2 Procedure of three involved algorithm

本课题组的王铜铜[14]等，在CNS程序原始代码的基础上实现MPI/OpenMP的两级并行后，在一个以MIC协处理器作为加速器的平台上，基于OpenMP 4.5尝试了上述方式来构建Offload模式下的异构程序。王铜铜等的工作显著提高了CNS程序在CPU和MIC上的单核计算性能， OpenMP并行效率高，在“天河二号”超级计算机上的大规模并行测试展示了良好的并行可扩展性，然而其CPU+MIC异构并行算法相对于纯CPU上MPI+OpenMP并行算法尚无性能加速。

通过分析，并参考同类研究，认为造成这种情况的重要原因之一是异构计算资源之间频繁的数据传输带来的开销影响了程序整体的性能。在上述的异构算法中，Offload进程的执行过程可以概括为图2(b)，可以看出，对于Offload进程，除了在时间推进步开始和结束时CPU和加速器端的数据传输和回收以外，每次当计算内核RK4执行到步骤②和④都需要将加速器端的中间计算结果传回CPU端进行MPI通信，再次传至加速器端继续计算。如图2(b)所示，计算内核RK4的内部，由步骤②和④引起的异构计算资源的PCIe数据传输共有16次，这种数据传输开销很大。另外，这也破坏了RK4在加速器端执行的连续性，使得RK4内部的OpenMP并行区无法尽可能地合并，增加了线程管理开销。为了便于描述，本文后面将这种Offload模式下，把部分任务子块整个地迁移到加速器上计算的异构算法称为direct-Offload算法(代码)。

3 基于内外子区域划分的异构算法

为此，不得不寻求新的方式来构建异构程序，提升程序在异构平台上执行的性能。结合前述direct-Offload程序的经验，从如何降低异构计算资源之间的数据传输开销出发，设计了新的异构算法。Yang等[6]在将基于有限差分的HPCG(high performance conjugate gradient benchmark)程序向“CPU+加速器(MIC)”的异构平台移植时，引入了一种对任务子块的内外子区域划分策略，使降低PCIe数据传输开销成为可能，进而使异构程序获得了较好的性能和加速。受此启发，得益于CNS程序本身规则的任务子块和结构化网格的便利，本文借鉴了这种内外子区域再划分的任务再划分策略，并结合4阶Runge-Kutta法这种显式时间推进算法的特点，成功设计了一种适合CNS求解器的基于内外子区域划分的ghost区域收缩式计算异构算法。

该算法极大地降低了Offload模式下异构程序CPU端和加速器端的数据传输开销，提升了CNS 程序在异构平台上的运行性能，我们从四个方面来介绍和讨论该算法：

1)任务子块的内外划分策略和ghost区域；

2)算法的执行过程；

3)ghost区域的宽度和收缩计算；

4)代码实现与负载均衡。

3.1 任务子块的内外划分策略和ghost区域

基于二维的情况来描述CNS程序的任务子块，图3(a)是原始MPI并行版本的程序的任务子块，本文对其进行如图3(b)所示的内外子区域再划分，任务子块被再划分成内部区域和外环区域。原来的任务子块是一个整体，包裹在子块外围的是MPI数据缓冲区，如图3(a)所示；进行内外子区域再划分后，原来的任务子块成为两部分：由加速器来计算的内部区域，和由CPU端负责的外环区域。值得注意的是，外环区域包含了原来的MPI通信数据缓冲区和实际计算的网格点两部分，CPU端的任务包括了计算和通信两部分。实际上，对于三维的任务子块，本文将立方体区域划分成内部的小立方块和外部具有一定厚度的空心立方壳两部分，其在二维情况下则退化为图中矩形内部区域和框形外环区域，因此，从二维情况来讨论已经足够表达基于内外子区域划分的异构算法的本质，同时，方便描述和理解。

所谓ghost区域，是指外环区域内边界内部保留的一定宽度的网格点区域，和内部区域外周界外部保留的一定宽度的网格点区域，如图3(c)和(d)灰色部分所示，分别称为inner ghost区域和outer ghost区域。外环区域的inner ghost区域将保存内部区域在外周界附近的计算数值，内部区域的outer ghost区域将保存外环区域在内边界附近的计算数值。当有两个子块分别使用两块加速器时，任务划分和执行的情况则如图3(e)所示。

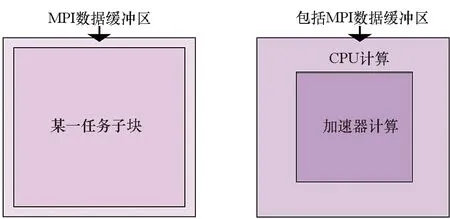
(a) 原始任务子块(a) Original task block (b) 内外子区域划分(b) Inner-out subdividing

(c) 外环区域(c) Outer halo region (d) 内部区域(d) Inner chunk region

(e) 两个任务子块内外划分后的情况(e) Two task blocks with inner-out subdividing图3 内外子区域任务划分策略Fig.3 Inner-out subdomain dividing strategy

3.2 算法的执行过程

基于上述内外划分策略，原来在整个任务子块执行的计算内核RK4，也随之划分为内部区域的RK4计算和外环区域的RK4计算，分别在加速器端和CPU端执行。

对于一个任务子块，重新设计的异构算法过程如图2(c)所示。

Offload进程首先初始化加速器端的执行环境，并将初值等传递到加速器端，该操作是在主循环的外部完成的。

随之进入时间推进主循环，在计算内核RK4开始之初，通过PCIe将内部区域边界附近的值传回CPU端，并保存在外环区域的inner ghost网格点上，同时，将外环区域内边界附近的值传至加速器端，并保存在内部区域的outer ghost网格点上。

随后加速器端独立地在内部区域上进行RK4的4阶计算，步骤②和④的MPI通信被完全交给了在CPU端执行的外环区域，在加速器端RK4的计算过程内部不再与CPU端通信，在outer ghost区域已经保存了需要的外环区域的值，从而完整的、连续地执行，直到一次循环结束。

CPU端同时进行外环区域RK4的计算，并且进行步骤②和④来与其他进程通信以填充子块外围MPI缓冲区的值，而inner ghost网格点提供计算外环区域内边界附近的差分所需的内部区域边界附近的值，这样CPU端也连续地执行其任务，直到一次循环结束前都不需要与加速器进行数据传输。

最终，一次循环结束时，将内部区域的计算结果从加速器端回收到CPU端用以收敛检验和文件输出等。

重新设计的异构算法，整个主循环的执行过程仅随着循环的开始和结束进行两次PCIe数据传输。参照直接将子块整个地迁移到加速器端计算的direct-Offload算法的过程，如图2(b)所示，重新设计的异构算法一方面减少了异构计算资源之间的PCIe数据传输次数；另一方面，也比直接将整个子块的数据在CPU和加速器端来回转移具有更少的数据传输量。

重要的是，得益于显式算法的便利性，对于CNS程序，这样的异构算法可以保证计算结果正确，因为ghost区域的宽度，是计算结果正确性的关键。

3.3 ghost网格点区域的宽度和收缩计算

以内部区域的outer ghost为例，来讨论ghost区域的宽度。设子块进行内外划分后，内部区域在x方向上有nnx+1个网格点，y方向上有nny+1个网格点，z方向上有nnz+1个网格点，二维情况下，nnz+1可以为1(或是任意正整数，设它为1 即可)。

由于CNS程序在xy方向的差分计算，在形式上没有任何区别，其ghost区域的宽度是一样的。设xy方向outer ghost区域的宽度都为Wg个数据点。从图1中可知，CNS程序在计算一个网格点在某一个方向的数值导数时，将使用该网格点前后各6个网格点的数值，xy坐标方向差分计算形式有如下形式：

Ai,j=f(Bi-1,j,Bi-2,j,Bi-3,j,Bi-4,j,Bi-5,j,Bi-6,j,Bi+1,j,Bi+2,j,Bi+3,j,Bi+4,j,Bi+5,j,Bi+6,j)

(5)

Ci,j=f(Bi,j-1,Bi,j-2,Bi,j-3,Bi,j-4,Bi,j-5,Bi,j-6,Bi,j+1,Bi,j+2,Bi,j+3,Bi,j+4,Bi,j+5,Bi,j+6)

(6)

式中，B表示泛指程序中某一变量，式(5)和(6)分别计算了变量B在xy两个方向的数值导数并赋值给了变量A和变量C。

在cacul_flux中，CNS程序对物理场变量(如速度、温度等)的空间x方向数值偏导数的计算，都具有上述式(5)的形式，y方向的数值偏导数的计算形式如式(6)所示。而cacul_Φ的计算，是对cacul_flux差分计算所得的结果，即通量项(F,G,H)，进一步差分得到F项的，其计算形式同样具有式(5)和(6)的形式。进一步，以x正方向的情况为例，规定内部区域(不包括ghost点)沿着x正方向的第一个网格点的i下标为0，下标沿着x正方向递增，那么其ghost区域在x正方向的最后一个点的i下标为nnx+Wg。在cacul_flux中，ghost区域能保障式(5)形式的差分能够正确计算的网格点的i下标的上界需要满足条件：i+6=nnx+Wg，显然可算得循环下标i的上界为nnx+Wg-6。

在计算完cacul_flux的结果的基础上进一步执行cacul_Φ，显然要保证cacul_Φ中式(5)形式的差分能够正确计算的网格点的i下标的上界需要满足条件：i+6=nnx+Wg-6，因此能够正确计算cacul_Φ的网格点的循环i下标的上界为nnx+Wg-12。

观察图2(c)不难发现，在RK4的第一阶计算中包含差分计算的函数就是cacul_flux和cacul_Φ这两个函数，第二阶计算在第一阶计算的基础上重复与第一阶类似的过程，因此第二阶计算只能在i上界为nnx+Wg-12的范围内进行。同理，第三阶计算只能在i上界为nnx+Wg-24的网格点范围内进行，第四阶计算只能在i上界为nnx+Wg-36的网格点范围内进行，第四阶计算完，计算结果正确的网格点的i下标的上界为nnx+Wg-48，式(5)和(6)有完全相同的形式，并且是以i,j号网格点中心对称的，所以i下标的下界和j下标的上下界都有上述“收缩”的规律。将这个ghost区域以12个网格点宽度，逐阶收缩的过程表示为图4，浅灰色表示最初的ghost区域，深灰色表示计算完一阶后向内收缩了一层。

图4 ghost区域的收缩计算Fig.4 ghost-region-shrinking computing scheme

显然，保证RK4的四阶计算结束后内部区域的网格点计算结果正确的条件是nnx+Wg-48=nnx，则有Wg=48。因此内部区域ghost网格点的宽度至少为48个网格点，外环区域的计算和内部区域的计算是一样的，可证其ghost区域的宽度也需满足这个条件。取ghost区域的宽度为48个网格点即可，我们没必要取更宽的ghost区域，因为更宽的ghost区域除了增加主循环开始时CPU和加速器之间的数据传输量，以及带来更多不必要的计算以外，没有任何意义。三维情况下，上述收缩计算在z方向同样执行，所以对于三维的立方块，ghost区域在xyz方向的宽度都为Wg=48。

值得注意的是，在这种算法中，应该保证外环区域和内部区域本身的大小，要使其能够提取足够的网格点来填充ghost区域的数值。

3.4 代码实现与负载均衡

OpenMP 4.5对Offload模式的异构程序开发与移植已经有较好的支持，通过合适的编译指导语句，便可以将代码段放在加速器端执行，并且支持数据异步传输等操作，同时支持多平台，代码具有良好的可移植性。在已有的CNS程序的MPI/OpenMP两级并行代码的基础上，基于OpenMP 4.5，实现了上述基于内外子区域划分的Offload模式的异构算法。为了叙述的方便，后面将基于内外子区域划分的Offload模式的异构代码称为subdomain-Offload算法(代码)。

MIC卡支持包括OpenMP在内的多种并行编程模型。将subdomain-Offload代码放在本课题组一个CPU+MIC结构的服务器单节点上进行调试和运行，并检验了代码执行和计算结果，与原来的纯CPU代码是完全一致的。

CNS程序本身子块具有相同的大小， 对于subdomain-Offload算法来说，将每一个进程的子块都进行相同的内外子区域划分，并将内部区域放在加速器端计算，外环区域放在CPU端计算，这样进程和进程之间仍是负载均衡的，而更重要的是CPU和加速器之间的负载均衡。

从subdomain-Offload算法的过程来讲，在主循环的一次执行过程中，CPU端的计算和加速器端的计算在RK4内部完全独立的执行，仅在主循环开始和结束的时候存在同步和进行PCIe数据传输。因此，通过控制内外子区域划分的比例调整CPU端和加速器端的负载分配，完全可以做到使一次主循环中的CPU端外环区域的计算及MPI通信和加速器端内部区域的计算在时间上几乎相等。本文通过实测对此进行了验证和分析。

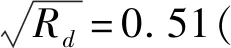
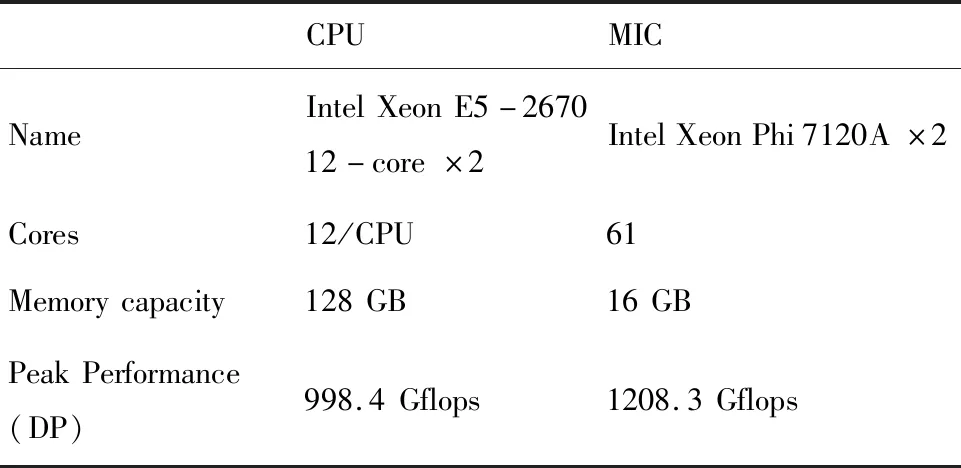
表1 服务器的配置Tab.1 The Configuration of the Server

(a) RK4函数单步执行时间(a) Single step execution time of RK4 function

(b) 程序执行总时间(b) Total program execution time图5 使用一块加速卡时的负载均衡Fig.5 Load balance tuning with one accelerator

由于CNS程序本身的任务子块都划分成了相同的网格点数，而直接将部分子块整个地传输到加速器端计算的direct-Offload算法，虽然可以调整CPU端和加速器端计算的负载，但是这种调整必须是以子块为单位的，在实际操作中，这其实是难以真正做到CPU和加速器之间达到负载均衡的。所以相对于direct-Offload算法，subdomain-Offload 算法有更好的负载均衡。

特别地，当负载均衡的时候，CPU 端的计算和MPI通信与加速器端的计算在时间上可以完全重叠，程序有更好的异构协同并行性。

4 性能测试与分析

进一步在表1配置的服务器上对subdomain-Offload算法的单节点性能进行了测试和评估。选取三种较大的数据规模，网格点数分别为2.88×106、5.76×106和11.52×106，在测试的过程中，CPU端和MIC卡上的核心全部都被用满，并关闭了CPU端超线程开关。测试了direct-Offload算法使用单块加速卡的情况，以及重新设计的subdomain-Offload算法使用一块和两块MIC卡的情况，同时，测试了只使用CPU核计算的MPI/OpenMP两级并行代码的情况作为对照。

4.1 性能测试

图6中蓝色图例是direct-Offload算法使用单块加速卡MIC的情况，红色图例是subdomain-Offload算法使用MIC的情况。结果显示，在测试的三种数据规模下，direct-Offload算法的程序执行总时间平均为subdomain-Offload算法执行总时间的5.9倍。subdomain-Offload算法相较于直接将部分子块整个传输到加速器端计算的direct-Offload算法性能有较大提升，subdomain-Offload算法相较于direct-Offload算法一方面极大地消除和降低了异构计算资源之间的数据传输，另一方面，subdomain-Offload算法比direct-Offload算法做到更好的负载均衡，这些对CNS程序在异构平台的性能提升是有效的。

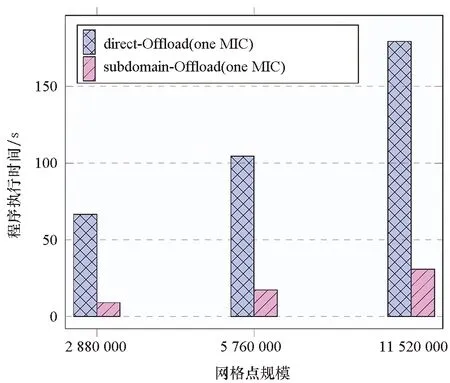
图6 相对于direct-Offload算法的性能提升Fig.6 Performance improvement over direct-Offload

图7是subdomain-Offload算法分别使用单块MIC以及两块MIC卡的情况。在单块加速卡的性能测试中，使用一块MIC加速卡计算内部区域，24个CPU核全部计算外环区域，任务分配如图3(b)所示，依据负载均衡，使内部区域的网格点的数目占总区域网格点数目的26%左右，理论上应获得的性能加速约为1.35倍。实际测试结果如图7中蓝色图例所示(黄色图例是纯CPU核计算的情况)：纯CPU计算的程序执行时间分别为三种规模下subdomain-Offload使用CPU+MIC计算执行时间的1.23倍、1.24倍、1.27倍，实际的性能加速低于理论的性能加速，造成实际性能加速低于理论性能加速的因素包括异构计算资源之间的数据传输开销，以及计算ghost网格点的额外开销等。

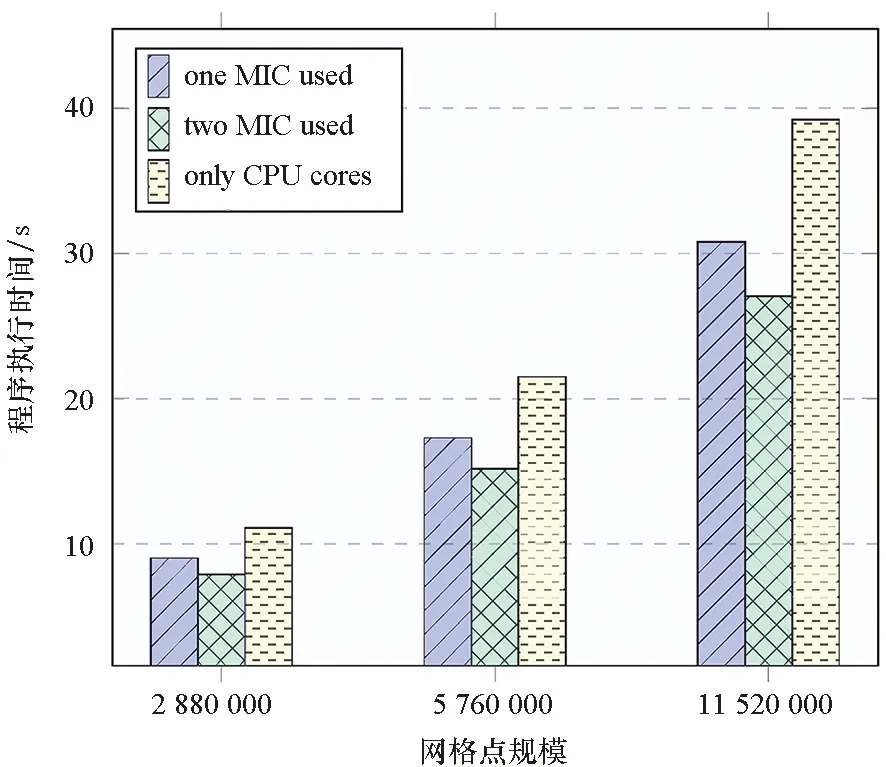
图7 服务器上subdomain-Offload算法的性能加速Fig.7 Acceleration of subdomain-Offload on server

在使用两块加速卡的性能测试中，任务分配如图3(e)所示，任务被分配到两个进程中，两块加速卡计算各自任务子块的内部区域，两块MIC加速卡共同承担总计算任务的42%左右，24个CPU核心此时承担的外环区域的计算任务约占总计算任务的58%，此时负载是均衡的，理论上，可以获得1.72倍左右的性能加速。实际测试结果如图7中绿色图例所示：纯CPU计算的程序执行时间分别为三种规模下subdomain-Offload使用CPU+2MICs计算执行时间的1.40倍、1.42倍、1.45倍。

结果表明，subdomain-Offload异构算法，使用MIC卡加速器时可以获得加速，在测试的服务器上，最大获得了1.45倍的性能提升。比较三种数据规模的结果，发现单节点计算的数据规模越大，性能提升相应增加，使用两块加速卡比使用一块加速卡能获得更多的性能提升。

4.2 问题分析

subdomain-Offload算法使CNS程序在异构平台上得到了性能提升，但加速效果并不理想，在测试的数据规模中，使用一块加速卡时的最大性能提升为1.27倍，使用两块加速卡的最大性能提升为1.45倍，原因有以下几个方面。

首先，测试节点上的MIC加速卡在CNS程序中能发挥的计算性能，较CPU能发挥的计算性能是更劣势的。结合图5，不难发现，随着Rd的增大，MIC上承担的计算任务增加，CPU端的计算任务减少，计算任务从CPU端转移到MIC上，MIC卡的任务执行时间剧烈的增加(图5 (a)中的蓝线比红线更陡)，图5 (b)中主循环的执行时间也随着MIC上任务的执行时间增加而剧烈增加，这说明节点由CPU主要承担计算转向MIC主要承担计算后，整个节点的等效计算能力是降低的。并且当负载均衡时，一块MIC卡在CNS程序中发挥的计算性能仅相当于CPU计算性能的35%(Rd=0.26时负载均衡，MIC的计算时间和CPU 相等)。这意味着使用一块加速卡最多也只能获得性能提升至1.35倍，两块卡最多提升至1.72倍，这还没有考虑数据传输等引起的开销。

其次，subdomain-Offload算法在一次时间推进步中，仍需进行两次PCIe数据传输，引起的开销是不可忽略的。在每一次主循环开始的时候，CPU端和加速器端需要通过PCIe交换ghost区域的数值，这是保证subdomain-Offload算法正确性所需要的。这不仅带来PCIe传输开销，对填充ghost区域的数值在传输前后进行打包与释放，以及ghost网格点本身也产生额外的计算，这些都将引入一些开销。二维情况下，任务子块的网格点总数为NX·NY·1(二维情况，可令NZ=1)，内部区域的网格点数为(NX·δ)·(NY·ξ)。δ和ξ分别为内部区域xy方向上的长度占整个任务子块对应长度的比例，即有Rd=δ·ξ。那么inner ghost网格点的数量可以表示为(2Wg+NX·δ)·(2Wg+NY·ξ)-NX·δ·NY·ξ，outer ghost区域的网格点数为NX·δ·NY·ξ-(2Wg-NX·δ)·(2Wg-NY·ξ)，则ghost区域网格点的总数为两者之和，可以整理为4Wg·(NX·δ+NY·ξ)。综上，引入的ghost网格点的总数所占任务子块网格点数的比例Pg可以表示为：

(7)

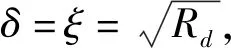
(8)

从式(7)或式(8)中不难发现ghost网格点数量占任务子块网格点数量的比例Pg是随着任务子块网格点数的增加而降低的，因此，为了使ghost网格点引起的开销对整个任务子块计算性能的影响减小，就需要设置较大的子块数据规模，如果我们在一个N=500的方形区域上，若Rd=0.26，那么由式(8)所估算出来ghost网格点所占任务子块总网格点数量比例将达到40%。这时由ghost网格点引起的传输和计算等开销对程序整体执行性能的影响将是十分明显的。可以通过增加子块网格点数规模来降低ghost区域带来的影响，但回收内部区域计算结果带来的传输开销是伴随着加速器端任务增加而增加的。

再次，内外子区域划分，造成CPU计算的外部区域的形状是不规则的，降低了CPU端计算的访存效率等，也是使异构程序性能受限的原因。

最后，测试平台上的Haswell CPU的计算能力也很强，其峰值性能接近单块MIC卡的峰值性能，因此CPU+MIC异构并行相对于纯CPU并行的性能加速效果不那么显著。

5 结论与未来工作

本文重新设计了高精度CFD求解器CNS在Offload模式下的异构程序，结合结构化网格下有限差分计算和4阶Runge-Kutta显式时间推进方法的特点，提出了一种基于对任务子块内外子区域再划分的“CPU+加速器”异构混合并行算法，即subdomain-Offload算法。该算法从降低异构计算资源之间的PCIe数据传输开销出发，同时改善了CPU和加速器之间的负载均衡，明显地提高了异构程序的单节点性能。测试和分析结果表明：

1)subdomain-Offload算法相对原有异构并行版本(direct-Offload算法)有平均5.9倍的性能提升，降低异构计算资源之间的数据传输开销，改善CPU和加速器的负载均衡对CNS异构程序的性能提升是显著的。

2)基于内外子区域划分的异构并行算法相较于纯CPU的MPI/OpenMP两级并行算法使用双Intel Haswell CPU(Xeon E5-2670，每CPU 12核)计算的情况，使用单MIC卡(Xeon Phi 7120A)时的最大性能加速为1.27倍，使用双MIC卡时的最大性能加速为1.45倍。

本文引入的基于内外子区域划分的异构协同并行算法可进一步推广到结构化网格下基于有限差分和显式求解偏微分方程的其他问题，具有良好的可迁移性。未来，将从提高CNS 程序在MIC加速器端的单核计算能力和整体计算性能着手，进一步提升subdomain-Offload异构算法的单节点性能，包括进行向量化、编译指令优化等。同时，将尝试将subdomain-Offload算法向其他结构的异构平台(如CPU+GPU)进行移植并观察其性能表现。