着陆缓冲气囊的无反弹设计方法研究

周 旋，周仕明，李道奎

(国防科技大学空天科学学院， 长沙410073)

1 引言

缓冲气囊在重装空投[1]和航天器软着陆[2]领域应用广泛，具有包装容积小、缓冲性能好、容易控制等优点[3]。 缓冲气囊按缓冲机理可分为3类：密闭型、排气型和组合型。 密闭型气囊不对外排气，主要通过内部气体的压缩和系统的多次反弹来消耗能量[4]，因此在缓冲过程中有效载荷不会直接触地；但由于反弹和翻滚不可避免，将导致有效载荷的最终姿态不可控，增加着陆的危险系数，须附加姿态调整、气囊移除和额外防护等设施。 排气型气囊在缓冲过程中首先进行压缩，当内压增加到一定阈值时排气口打开，通过排出气体带走大部分的能量[5]，所以能够实现有效载荷的无反弹着陆。 与密闭型相比，排气型气囊通过一次压缩即可实现着陆，缓冲效率高，但系统极易以一定的终了速度硬着陆，对有效载荷造成冲击。组合型气囊通常为双气室，外气囊为排气型，内气囊为密闭型[6]。 它综合了前两种气囊的优点，能够在消除系统反弹的同时，避免直接触地的危险。但是，无论是排气型还是组合型气囊，都有可能导致系统反弹，带来姿态不可控、二次冲击等危害，须在设计气囊时避免反弹。

目前对缓冲气囊的研究主要集中于缓冲机理和缓冲性能[7-9]，多采用解析分析和仿真分析方法，前者效率更高。 其中，在对排气型和组合型气囊系统缓冲性能进行分析和优化时考察最多的性能指标是气囊内压和冲击过载[2，9-10]，未有将是否反弹作为性能指标的。 针对气囊反弹问题的研究也较为少见，现有的思路是通过对多种规格的气囊进行分析计算，从中选择在缓冲过程中未发生反弹的气囊模型[11]。 该方法效率较低，得到结果也并不是最优的，而且难以保证其他缓冲性能指标。 因此，需要更有效的气囊无反弹设计方法。

本文通过对气囊在缓冲过程中的变形进行假设，并基于牛顿第二定律和热力学方程建立适用多种不同形状的排气型气囊的动力学解析模型，并在此模型的基础上提出一种着陆缓冲气囊的无反弹设计方法，以无反弹为约束条件，通过优化求解来获得无反弹、冲击加速度更小、触地速度更小的缓冲气囊模型。

2 着陆缓冲气囊系统的动力学模型

排气型气囊着陆缓冲过程可抽象为4 个阶段：充气、自由下落、压缩和排气。 如图1 所示。

1)气囊充气阶段(a-b)：整个系统降落到一定高度时，气囊开始充气。

2)自由下落阶段(b-c)：完成充气后，气囊的热力学状态保持不变。 在气囊触地之前，整个系统不断下落，下落一定高度后降落伞开始脱离。

3)气囊压缩阶段(c-d)：气囊触地后受到地面的反作用力压缩变形，内部气压不断增大。

4)气囊排气阶段(d-f)：当气囊内压达到设定的阈值时排气口打开，气囊开始排气，排出的气体带走大部分的能量。 随着缓冲的进行，有效载荷的速度不断降低，最后静止，有效载荷安全着陆。

图1 缓冲着陆过程Fig.1 Impact attenuating process

因此，气囊系统的缓冲性能主要体现在气囊的压缩和排气阶段，下面对这2 个阶段对进行具体研究，建立缓冲气囊的动力学模型。

2.1 模型建立

着陆器软着陆时一般会控制其水平速度趋于0，因此可假设有效载荷竖直下落，没有水平速度，同时考虑到气囊织物的质量远小于有效载荷，从而简化得到图2 所示的单气囊系统，沿竖直方向(定义向上为正)建立整个系统的平衡方程如式(1)：

图2 单气囊系统缓冲过程Fig.2 Cushioning process of single airbag

式中，Pbag为气囊气体压力， Patm为大气压，At为气囊与地面接触面积，M 为有效载荷的质量，a 为有效载荷的加速度。 经过时间步Δt，有效载荷的速度ut如式(2)：

式中，ut-1为前一个时间步有效载荷的速度。进而得到有效载荷的位移ht如式(3)：

式中，ht-1为前一个时间步有效载荷的位移。有效载荷和气囊之间的能量传递效率与压缩过程中气囊本身几何形状的变化有关。 直接进行“流固耦合”分析能够得到气囊的变形过程，但是耗时太长，在方案设计阶段往往对气囊的变形过程进行简化。 圆柱形气囊制造工艺简单，实际应用最为广泛，以其为例进行说明。

如图2 所示，圆柱形气囊在压缩过程中可假设其轴线长度保持不变，横截面从初始的圆形变为两端为半圆的圆角矩形，且变形前后横截面周长不变，如式(4)[12]：

式中，D0为圆柱形气囊横截面的初始直径，也就是气囊的初始高度； Dt为变形后气囊的高度；Lt为气囊横截面接触长度。 压缩后气囊的高度如式(5)，可通过有效载荷的位移来求得。

设圆柱形气囊的轴线长度为L0，则压缩过程中气囊与地面的接触面积和气囊体积如式(6)、(7)：

与上面的方法类似，对于不同形状的气囊可以给出相应的变形假设，从而得到缓冲过程中气囊的高度变化与其触地面积和体积之间的关系。如表1 所示，给出了6 种常用的不同形状的气囊在缓冲过程中的变形假设。 对应的各种形状气囊的结构形式如图3 所示。

根据气囊变形假设得到了气囊容积Vt后，气囊气体密度也随之确定，可以使用标准气体动力学方程来确定气囊内部压力，从而判断排气口是否打开。 为简化模型，做出以下假设：

1)假设气囊内的气体为理想气体；

2)气囊缓冲过程是等熵过程的。

气囊压缩和排气过程速度快、时间短，来不及与外界进行热交换，可看作是绝热过程。 并且排气口流程短，摩擦阻力可忽略不计，所以不可逆效应的影响很小。 因此等熵过程假设是合理的。

表1 不同形状气囊的变形假设Table 1 Deformation assumptions for different shapes of airbags

图3 各种形状的气囊Fig.3 Various shapes of airbags

设气囊排气口打开的压力阈值为Popen， 当Pbag≤Popen时，气囊未排气，前后两个时间步的气体质量相等( mt＝mt-1)。 那么，根据等熵过程假设可求得气囊的其他状态参数。

当Pbag＞Popen时，排气口打开，气囊开始排气，设当前时间步下排出的气体质量为Δm，则当前时刻气囊中气体质量为mt＝mt-1- Δm。 由于气囊内气体的平均流速接近于零，所以气囊排气过程可以看作是标准喷管的流动过程。 设气囊压力为上游压力，下游的局部大气压力为排气口处压力，则排气口上下游的压力之比如式(8)所示：

根据质量流量方程，同时考虑到排出气体的流速可能会达到声速，排出气体质量如式(9)、(10)[7]：

1)当λ ≥0.528(亚音速流)时，

2)当λ ＜0.528(音速流)时，

式中，CD为孔口流量系数， Aor为排气口面积，RGAS为个别气体常数， T0是初始时刻气囊气体温度，γ 是气囊气体的比热比， P0是初始时刻气囊内压。 孔口流量系数表征了孔流固有的低效率性，这是由于在气流通过孔口时因为摩擦和流体粘性效应产生了一定的能量损失，并且其与压力比存在如式(11)所示的关系[8]：

气囊排气后，根据等熵过程假设求得气囊内压如式(12)，进而可得到气囊的其他状态参数。

需要说明的是，一旦排气阀打开就不会关闭，即排气阀打开前，气囊内压需要与阈值压力进行比较来判断是否排气；而阀门打开后，需要与大气压比较来判断是否排气。

2.2 模型验证

圆柱形气囊(卧式)的模型参数如表2 所示，假设在排气过程中排气口的面积保持不变，运用建立的解析模型对其缓冲过程进行分析，并采用控制体积法[14](CV 法)建立有限元模型对解析模型计算结果进行验证。 圆柱形气囊的有限元模型如图4 所示。 解析模型和有限元模型的计算结果对比如图5 所示。

从图5 中可以看到，缓冲过程中的气囊内压、气囊体积、气体质量、有效载荷加速度、有效载荷速度和有效载荷位移6 个参数，解析模型计算结果与有限元模型计算结果均吻合得较好。 其中，气囊内压的偏差最大，约为11.99%，在可接受的范围内。 因为气囊变形是通过假设得到的，所以气囊体积必然存在偏差，进而导致了最大气囊内压偏大。 最大冲击加速度的偏差约为0.33%，小于气囊内压的偏差，这是因为有效载荷的加速度不仅由气囊内压决定，还与触地面积有关。 上述结果表明，本文所建立的动力学解析模型合理，精度较高。

表2 圆柱形气囊系统模型参数Table 2 Parameters of cylindrical airbag model

图4 圆柱形气囊的有限元模型Fig.4 Finite element model of cylindrical airbag

图5 解析模型与有限元模型的计算结果对比Fig.5 Comparison of calculation results between the analytical model and the finite element model

图6 气囊系统的缓冲过程Fig.6 Cushioning process of the airbag system

另一方面，从图6 可以明显看到，该气囊系统在缓冲过程中发生了反弹，这必将带来二次冲击，并且增大系统着陆的危险系数，可能会导致翻滚和倾覆，因此该气囊模型有待优化。 当排气口直径为0.152 m 时，从图6 中不难发现，气囊系统没有发生反弹，而是以一定的速度硬着陆。 这是由于排气口面积变大，气囊未完全吸收有效载荷的能量而导致的。 因为解析模型没有考虑有效载荷与地面碰撞之后的运动，所以0.207 s 时停止了计算。 在有效载荷触地之前，解析模型与有限元模型的计算结果吻合较好。 触地之后，气囊与地面的接触面积没有明显变化(图6)，气囊内压也没有明显变化(图5(b))，但是有效载荷的加速度却突然增大(图5(d)所示)，显然这是由于有效载荷与地面之间的碰撞而导致的。 如图6 所示，由于硬着陆的发生，气囊系统在着陆后期会有微幅的振荡，有效载荷略有弹起；在0.3 s 时，气囊也离开地面很小的距离。 从图5(d)还可以看到，有效载荷硬着陆产生的最大加速度略小于缓冲过程中的最大加速度。 根据解析模型的计算结果，有效载荷硬着陆时的速度约为1.0 m/s。

显见，当触地速度更大时，硬着陆而产生的加速度也将更大，甚至超过缓冲过程中的最大加速度；所以，有效载荷的触地速度应越小越好。 因而，有效载荷触地速度的大小，反映的也是有效载荷在着陆过程中所受冲击加速度的大小。

3 无反弹优化设计方法

3.1 无反弹设计思路

设计无反弹着陆缓冲气囊的基本思路如图7所示。 采用建立的解析模型进行优化设计。

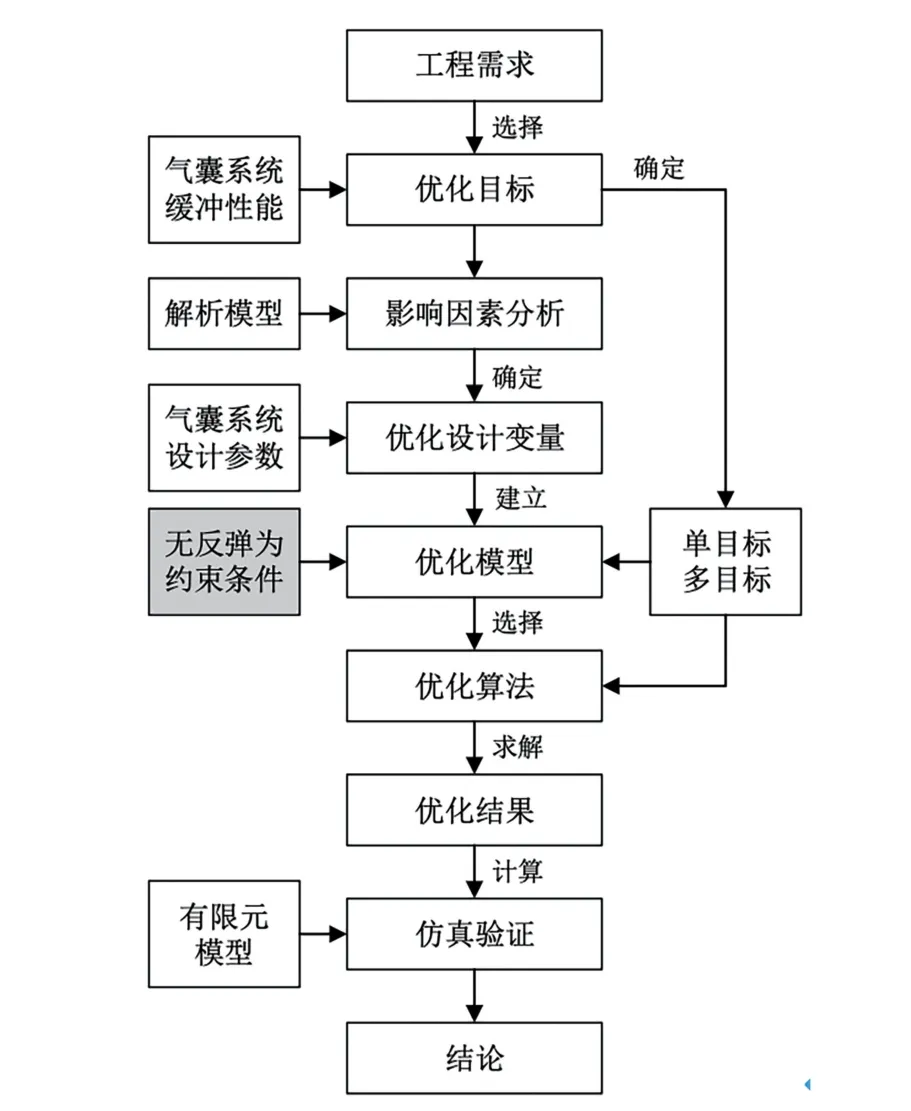
图7 无反弹着陆缓冲气囊的设计思路Fig.7 Design idea of impact attenuating airbag without rebound

3.2 优化数学模型

3.2.1 优化目标

1)气囊织物强度。 气囊在缓冲过程中是否会破裂，主要受气囊内压的影响，因此选择气囊最大内压作为评价指标，以保证气囊织物的强度要求。

2)冲击过载。 选择缓冲过程中的最大冲击加速度作为评价指标。

3)触地速度。 在排气过程中，若气体流速过快，没有完全吸收有效载荷的能量，那么将导致其以较大速度触地，从而产生较大的冲击。 因此选择有效载荷的触地速度作为评价指标。

4)是否反弹。 若气囊排气过慢，可能会使有效载荷反向加速，导致系统反弹。 因为有效载荷并没有直接触地，所以定义这种情况下的触地速度为0。 显然，当有效载荷有反向位移时即表明系统发生了反弹，因此可以通过判断每个时间步下有效载荷的位移的正负(即位移的方向)来获取系统的反弹信息。

表3 气囊缓冲性能的评价指标及其求解方法Table 3 Evaluation index of airbag cushioning performance and its solving method

通过上述分析，确定了气囊缓冲性能的4 个评价指标，求解方法如表3 所示。 这些性能指标可以作为优化设计的优化目标或约束条件。 不同需求和工况下，优化目标可能不一样，可以根据实际需求进行选取。 一般来说，有效载荷的最大冲击加速度和触地速度均越小越好。 因此，可以选择这两个参数作为着陆缓冲气囊的优化目标。

3.2.2 设计变量

由于气囊的设计参数较多(表2)，直接优化难度大，耗时长，因而应当通过影响因素分析对气囊缓冲性能的关键影响参数进行筛选。

圆柱形气囊的主要设计参数有气囊横截面直径D0、气囊长度L0、排气口直径Dor和排气阈值压力Popen。 对上述参数设计了4 因素4 水平的正交实验表L16(44)，如表4 所示。 运用本文建立的解析模型对这16 组气囊的缓冲性能进行求解，计算结果如表5 所示。 其中，触地速度取绝对值，不考虑其方向。 运用极差分析方法对上述16 组实验设计的结果进行分析，求得圆柱形气囊设计参数对其缓冲性能影响力的大小和正负，如图8 所示。

表4 正交实验表Table 4 Orthogonal experiment table

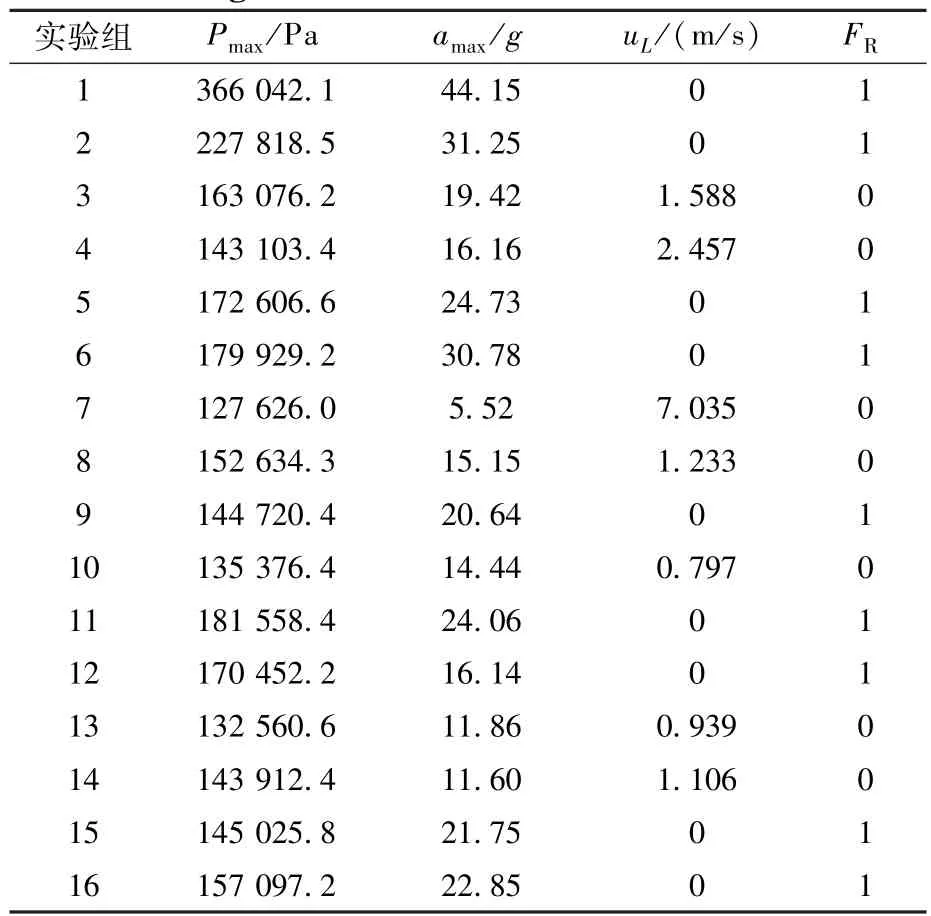
表5 正交实验设计的计算结果Table 5 The calculated results of orthogonal experiment design

总的来看，排气口直径对气囊缓冲性能的4个指标的影响均是最大的，其中对气囊最大内压、最大冲击加速度和是否发生反弹这3 个指标是负影响，对有效载荷的触地速度是正影响。 这表明排气口直径越大，气囊最大压力和最大冲击加速度越小、系统越不容易发生反弹，而触地速度越大。 这是因为排气口直径越大，排出的气体越多，气囊压缩更快，所以气囊内压更低，进而使得缓冲过程中的冲击加速度更小，更不容易发生反弹，从表5 中也能直接观察到这一点。 另一方面，正因为排气过快，有效载荷的能量吸收不完全，将导致其触地速度过大。 这也体现了触地速度与是否发生反弹这两个指标之间的关系：若有效载荷直接触地，则系统不会发生反弹；若气囊发生反弹，那么有效载荷不会直接触地。 图8(c)和图8(d)证明了这一点，即4 个设计参数对触地速度和是否发生反弹这两个指标的影响方向刚好相反。 因此，也可以使用有效载荷的速度是否反向来判断系统是否反弹，这与使用位移是否反向来评价是等价的。 从图8 中还可以看到，气囊长度对气囊缓冲性能4 个指标的影响均较小。

分别来看，如图8(a)所示，4 个设计变量对于气囊最大压力均为负影响，除了排气口直径外，气囊横截面直径对缓冲过程中气囊的最大内压也有较大影响，这是因为横截面直径D0的增加将增大气囊的体积和缓冲行程，导致内压降低。 从图8(b)中可以看到，除了气囊长度外，其他3 个参数均为负影响，这与对气囊最大内压的影响规律略有不同，主要是因为随着气囊长度L0的增加，气囊的体积增大，虽然缓冲过程中的气囊最大内压降低了，但由于与地面的接触面积增大了，所以最大冲击加速度增加了。 这一结果也说明气囊长度对接触面积的影响要大于其对气囊内压的影响。 从图8(c)中可以看到，除了排气口直径外，气囊横截面直径和排气阀开启压力也对缓冲过程中气囊的最大内压有较大影响。 从图8(d)中可以看到，系统是否发生反弹主要受排气口直径的影响。

根据以上分析计算最终得到，圆柱形气囊的排气口直径、横截面直径和排气阈值压力这3 个参数对最大气囊内压、最大冲击加速度、触地速度和是否反弹这4 个缓冲性能指标的影响较大，可作为优化的设计变量。

3.2.3 优化模型

着陆缓冲气囊的优化模型可抽象为式(13)：

图8 设计变量对气囊缓冲性能的影响Fig.8 Influence of design variables on the airbag cushioning performance

式中， f(X) 为目标函数， g(X) 为约束条件函数，可以根据具体问题分别从表3 中选择，对于无反弹着陆缓冲气囊的优化来说，其中最关键的就是定义约束条件FR＝0；xi为设计变量，即气囊的设计参数，可以根据工程经验或影响因素分析来确定； ¯x 和x-分别为变量取值的上下限。

4 着陆缓冲气囊的无反弹多目标优化

根据第2 节的分析计算可知，表2 中的圆柱形气囊在缓冲过程中明显发生了反弹，且最大冲击加速度达到了近30g，以其为例进行着陆缓冲气囊的无反弹优化设计。 选择气囊的排气口直径、横截面直径和排气阈值压力作为优化的设计变量，有效载荷的最大冲击加速度和触地速度最小作为优化目标，系统无反弹和最大气囊内压小于初始模型的最大内压作为约束。 根据战技指标的要求[9]，并考虑一定的安全系数，确定最大冲击加速度≤12.0g。 根据前面的分析，触地速度为1.0 m/s 时产生的冲击加速度小于最大冲击加速度，因此取触底速度≤1.0 m/s。 将表2 中的气囊参数作为优化的初值，最终建立无反弹着陆缓冲气囊的多目标优化数学模型如式(14)：

（3）图像数据在服务器上的上传和下载过程都在服务器端完成，这种设计增加了服务器端的负担，影响了针对数据仓库的上传、检索和下载速度。

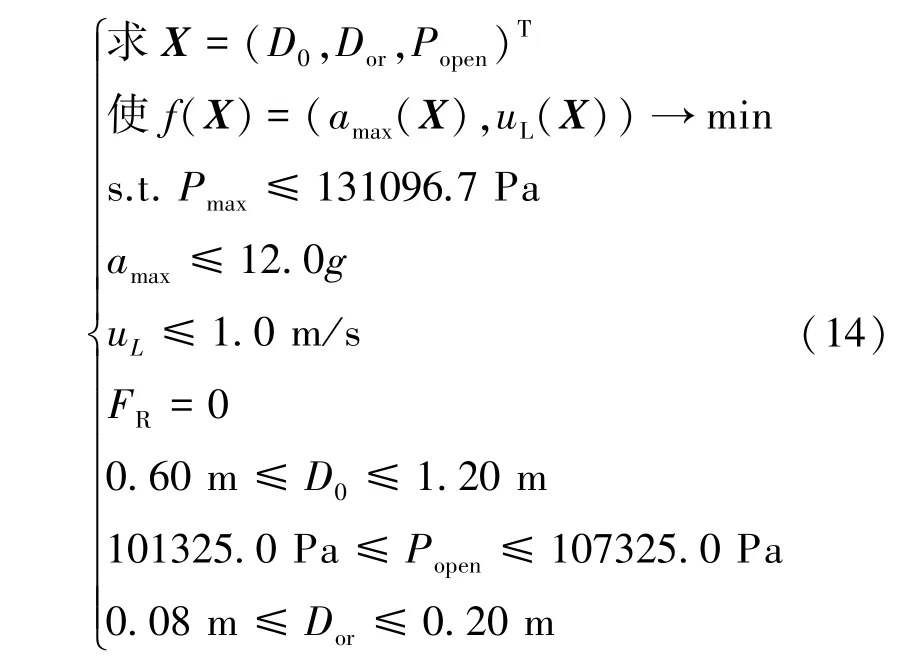
选择NSGA-II[15](带精英策略的非支配排序遗传算法)对无反弹着陆缓冲气囊的多目标优化问题进行求解。 通过多次测算确定种群大小为20，进化代数为50，交叉变异的概率为0.9。 经过1000 次迭代得到无反弹着陆缓冲气囊多目标优化的一组Pareto 最优解集如图9 所示，共147 个最优设计点，优化后设计变量的取值范围如式(15)所示：

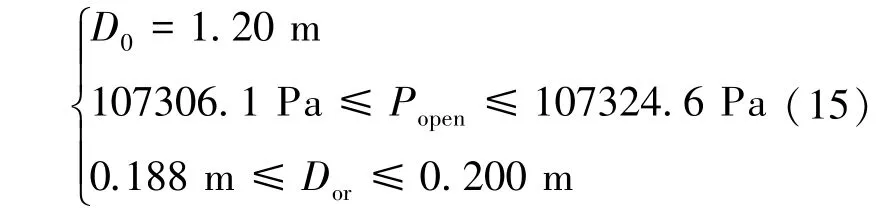
图9 Pareto 最优解集Fig.9 Pareto optimal solution set

式(15)表明优化迭代的方向，即气囊横截面直径D0、排气阈值压力Popen和排气口直径Dor均增大，与影响因素分析的结果一致。 选取Pareto 最优解集中的两个优化数据点(如图9 所示)，得到优化后的气囊参数如表6 所示。 相较于优化前的气囊，气囊的横截面直径均变为1.2 m，排气阈值压力均增大了约4.0 kPa，排气口直径分别变为原来的2.35 倍和2.50 倍。 气囊尺寸变大使得气体体积变大，排气阈值压力变大使得气囊对有效载荷动能的吸收更充分，排气口直径增大导致排出气体的质量流量增大，因而缓冲过程中气囊最大内压和有效载荷最大冲击加速度明显降低，最大内压分别降低了36.32%、37.74%，最大冲击加速度分别降低了58.83%、61.92%。 由于排气口面积变大，触地速度有所提高，但小于1.0 m/s。

优化前后有效载荷位移对比如图10 所示，显然优化后的模型没有发生反弹。 同时对优化后气囊模型进行仿真分析，计算结果如图11 所示，可以看到气囊系统没有发生明显反弹，着陆后期的微幅弹起是由于硬着陆而导致的。 虽然有效载荷的位移反向了，但气囊织物并有没有离开地面，因此系统的姿态将不会再发生变化，更不会出现翻滚和倾覆，同时也表明硬着陆产生的冲击加速度很小，根据有限元分析的结果，优化模型-1 和优化模型-2 因硬着陆而产生的冲击加速度分别为3.93g 和5.53g，均不到缓冲过程中最大冲击加速度的50%。

表6 优化前后气囊模型参数及其缓冲性能指标Table 6 Parameters and cushioning performance of airbag model before and after optimization

从图10 中还可以看到，无论是优化前的气囊还是优化后的气囊，解析模型的计算结果与有限元模型的仿真结果均吻合得较好，说明计算结果正确可信。 综上所述，优化后的气囊不仅没有发生反弹，且其他缓冲性能也更优，表明了所提无反弹设计方法的有效性与可行性。

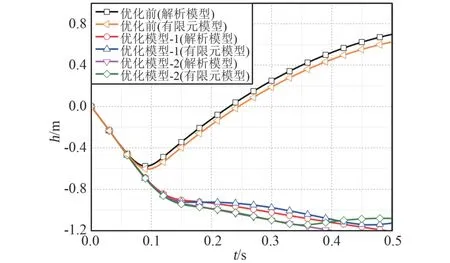
图10 优化前后有效载荷的位移Fig.10 Payload displacement before and after optimization

图11 优化模型的有限元仿真分析结果Fig.11 Finite element analysis of optimized models

5 结论

1)本文给出了6 种不同形状气囊的变形假设，建立了适用于多种构型气囊的缓冲过程动力学解析模型。 基于该模型，提出了着陆缓冲气囊的无反弹设计方法。 该方法以无反弹为约束条件，通过优化来获得无反弹的缓冲气囊模型。 运用此方法对圆柱形气囊进行无反弹多目标优化设计，得到了无反弹的、缓冲性能更优的圆柱形气囊，且优化前后气囊模型的解析计算结果与有限元仿真结果均吻合较好，表明所提方法具有可行性和有效性。

2)该设计方法定义了气囊缓冲性能的4 个评价指标：最大气囊内压、最大冲击加速度、有效载荷触地速度和有效载荷位移的方向。 在研究影响圆柱形气囊缓冲性能指标的关键设计参数时发现：气囊排气口直径、横截面直径和排气阈值压力的影响较大，其中排气口直径的影响最大；而气囊长度的影响很小。

参考文献(References）

[ 1]王红岩， 洪煌杰， 李建阳， 等. 空降车缓冲气囊系统特性仿真及其参数优化方法研究[J]. 兵工学报， 2012， 33(12)： 1461-1466.

Wang H Y，Hong H J，Li J Y， et al. Research on simulation and optimization of cushion characteristic of airbags for airborne vehicle[J]. Acta Armamentarii，2012，33(12)：1461-1466.(in Chinese)

[ 2] Willey C， Sandy C， Welch J， et al. Impact attenuating airbags for earth and planetary landing systems[C]/ /AIAA SPACE 2007 Conference ＆ Exposition. Long Beach， California： AIAA 2007-6172， 2007.

Han H S， Wang Y R， Jiang Y P， et al. Characteristics and application of deep-space explorer landing impact attenuation system[J]. Spacecraft Engineering， 2012， 21(03)： 7-23.(in Chinese)

[ 4] Northey D， Morgan C. Improved inflatable landing systems for low cost planetary landers[J]. Acta Astronautica. 2006， 59(8-11)： 726-733.

[ 5] Lee C， Rosato N， Lai F. An investigation of improved airbag performance by vent control and gas injection[C]/ /11thAerodynamic Decelerator Systems Technology Conference. San Diego， CA， USA： AIAA 91-0892-CP， 1991.

[ 6] Tutt B， Gill S， Wilson A， et al. A summary of the development of a nominal land landing airbag impact attenuation system for the Orion crew module[C]/ /20thAIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Seattle， Washington： AIAA 2009-2922， 2009.

[ 7] Cole J K， Waye D E. BAG： A code for predicting the performance of a gas bag impact attenuation system for the PATHFINDER lander[R]. Albuquerque， NM： Sandia National Laboratories， SAND93-2133， 1993.

[ 8] Do S. An Airbag-Based Crew Impact Attenuation System for the Orion Crew Exploration Vehicle [D]. Massachusetts Avenue， USA： Massachusetts Institute of Technology， 2011.

[ 9] 温金鹏， 李斌， 谭德伟， 等. 考虑织布弹性的软着陆气囊缓冲特性研究[J]. 振动与冲击， 2010， 29(2)： 79-83.

Wen J P，Li B，Tan D W，et al. Cushioning characteristics of a soft landing airbag with elastic fabric[J]. Journal of Vibration and Shock， 2010， 29(2)： 79-83.(in Chinese)

[10] Tutt B A，Sanders J M，Myneni S. Application of optimization software to aid the design of an airbag decelerator system[C]/ /17thAIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Monterey， California： AIAA 2003-2150， 2003.

[11] Alizadeh M， Sedaghat A， Kargar E. Shape and orifice optimization of airbag systems for UAV Parachute landing[J]. International Journal of Aeronautical and Space Sciences， 2014，15(3)： 112-121.

[12] Esgar J， Morgan W. Analytical study of soft landings on gasfilled bags[R]. Cleveland， Ohio： Lewis Research Center，NASA Technical Report R-75， 1960.

[13] Bown N W， Darley M G. Advanced airbag landing systems for planetary landers[C]/ /18thAIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Munich， Germany： AIAA 2005-1615， 2005.

[14] 黄国， 李玮洁. 缓冲气囊研究方法进展[J]. 力学研究，2013， 2： 1-6.

Guo H， Li W J. Progress of research method on the buffering bags[J]. International Journal of Mechanics Research，2013，2： 1-6.(in Chinese)

[15] Deb K，Pratap A，Agarwal S，et al. A fast and elitist multiobjective genetic algorithm： NSGA-II[J]. IEEE Transactions on Evolutionary Computation， 2002， 6(2)： 182-197.