薄壁圆管开口式伸展臂卷绕过程力学特性分析

王思聪，商红军，郭宏伟，刘荣强，史 创*

(1. 哈尔滨工业大学机电工程学院，哈尔滨150001； 2. 中国空间技术研究院总体部，北京100094)

1 引言

空间薄壁式自展开伸展臂由于其轻质、高收纳比、自展开等特性，广泛应用于航天多个领域，例如Hubble 望远镜太阳翼支撑杆、国际空间站太阳翼支撑杆、NanoSail-D 太阳帆伸展臂、Apollo-15伸展臂等[1-3]。 由于该种伸展臂具有大尺度、大变形、柔性等特征，必须对其卷绕过程的力学特性进行分析。

Ross 等[4]通过多体动力学软件绘制了圆管开口式伸展臂卷绕位移、卷绕扭矩与时间的关系曲线并进行了分析。 楚中毅等[5]对透镜式缠绕肋展开态及展开过程力学特性进行了解析计算，并对缠绕肋及释放机构的结构尺寸参数进行了多目标优化。 张展智等[6]对圆管开口式伸展臂卷绕方式进行了研究，对过渡段曲率进行了拟合，通过ABAQUS 软件分析了不同卷绕方式、不紧密卷绕、摩擦因数等因素对伸展臂自由展开过程的影响。 陈务军等[7-10]通过ABAQUS 软件对透镜式缠绕肋展平卷绕过程中应力应变进行了计算分析，总结出各参数变化对缠绕肋力学特性的影响规律，并通过试验进行了验证。

上述研究对透镜式结构展收过程有较多分析，但较少涉及薄壁圆管开口式结构，尤其对该种结构在卷绕过程中应变能、驱动力矩、应力分布的研究甚少。 另外，由于卷绕过程中应变能、驱动力矩对伸展臂尺寸参数变化的敏感程度对伸展臂的设计有着重要影响，且过高的应变能易导致材料的失效，因此分析伸展臂尺寸参数的变化规律显得尤为重要。

本文基于由各项同性材料制成的薄壁圆管开口式伸展臂，假设材料在变形过程中为弹性体，通过推导薄壁圆管开口式伸展臂总应变能、驱动力矩公式，在ABAQUS 中建立有限元模型，分析伸展臂卷绕过程中总应变能、驱动力矩的变化规律，研究总应变能、驱动力矩对伸展臂各项尺寸参数变化的敏感程度。 同时根据第四强度理论分析伸展臂最大Von Mises 等效应力点的位置及其在卷绕过程中的变化规律，提出对伸展臂设计具有指导性意义的结论。

2 薄壁圆管开口式伸展臂卷绕机理

伸展臂收拢过程如图1 所示，收拢过程中每段微元依次经历3 个变形阶段：①当远离卷轴时微元处于自由状态阶段(自由段)；②随着卷轴的卷绕运动，微元进入过渡段后曲率逐渐减小直至完全展平，此过程中微元的展平过程作为纯弯曲变形处理，过渡段各部分横截面均看做标准圆弧；③当微元完全展平后随即向卷轴卷绕(卷绕段)，卷绕过程中卷轴中心与伸展臂自由状态下的形心分别位于伸展臂壳体两侧(反向卷绕)。

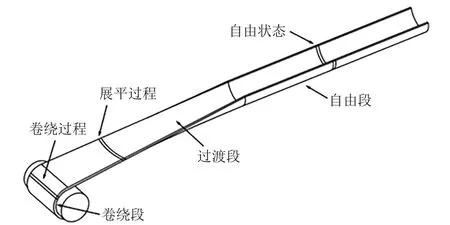
图1 伸展臂收拢过程微元变形Fig. 1 Element deformation during boom coiling process

3 伸展臂收拢过程应变能分析

3.1 伸展臂收拢过程应变能解析分析

根据第2 节中的假设，伸展臂微元在收拢过程中各处变形为纯弯曲，且变形过程中截面微元始终为标准圆弧。 根据材料力学相关理论，弯曲应变能Ei为式(1)(参变量如图2 所示)：

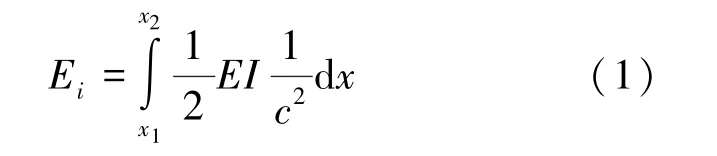
图2 弯曲应变能计算微元Fig.2 Calculation element of bending strain energy

伸展臂总应变能Es为收拢段应变能Ew与过渡段应变能Et之和。 因收拢过程可拆分为展平过程与卷绕过程且二者之间影响很小，因此收拢段应变能Ew为展平应变能Ef与卷绕应变能Eb之和。 因此总应变能Es为式(2)：

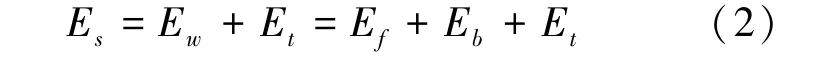
伸展臂横截面几何参数如图3 所示，图中Izz为横截面微元展平惯性矩沿卷绕长度的积分，如式(3)所示。

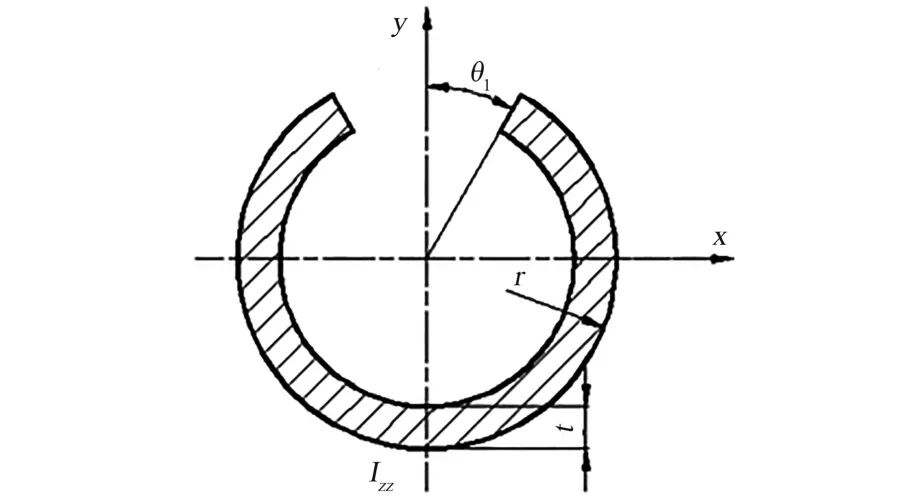
图3 伸展臂横截面尺寸参数Fig.3 Cross-section parameters of boom

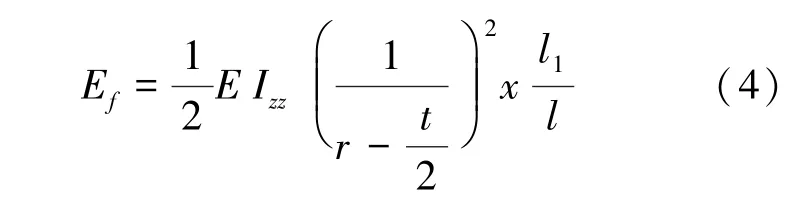
式中x 为展平过程中性面长度，如式(5)。 l1为已卷绕部分长度，l 为伸展臂总长度。

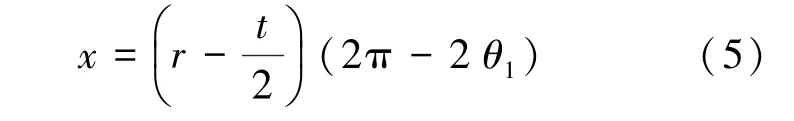
伸展臂卷绕过程纵截面参数如图4 所示，卷绕后伸展臂中性面近似为阿基米德螺旋线。

图4 伸展臂纵截面尺寸参数Fig.4 Longitudinal-section parameters of boom

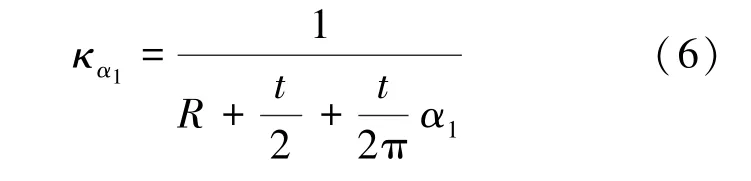
已卷绕长度l1为式(7)：

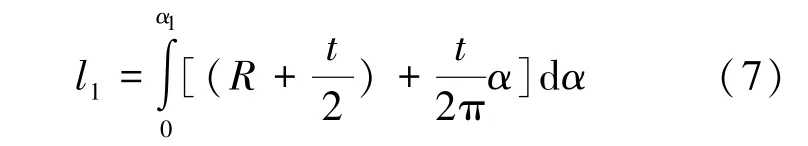
因此根据式(1)伸展臂卷绕l1长度时，其卷绕应变能Eb为式(8)：

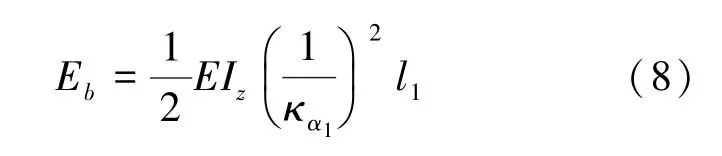
其中，卷绕过程弯曲截面惯性矩Iz为式(9)：

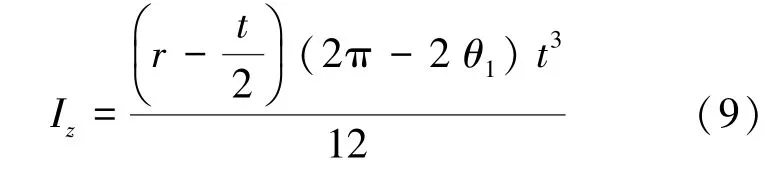
因过渡段伸展臂曲率变化复杂，因此过渡段应变能Et通过有限元仿真方法求出。

综上，根据(2)式，伸展臂卷绕l1长度时总应变能Es为式(10)：

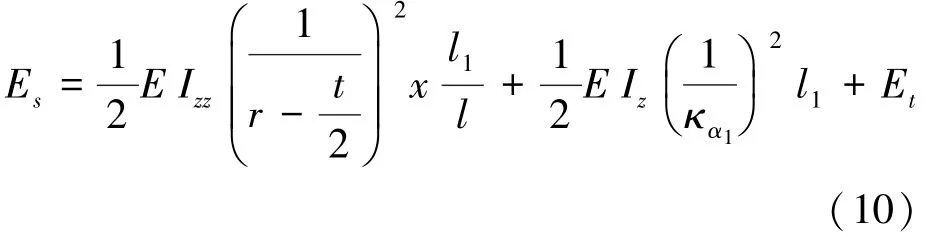
由上述关系并取表1 中参数，通过MATLAB编程计算，可得到已卷绕长度l1从0 变化至2 m过程中总应变能Es随l1变化过程的计算结果。

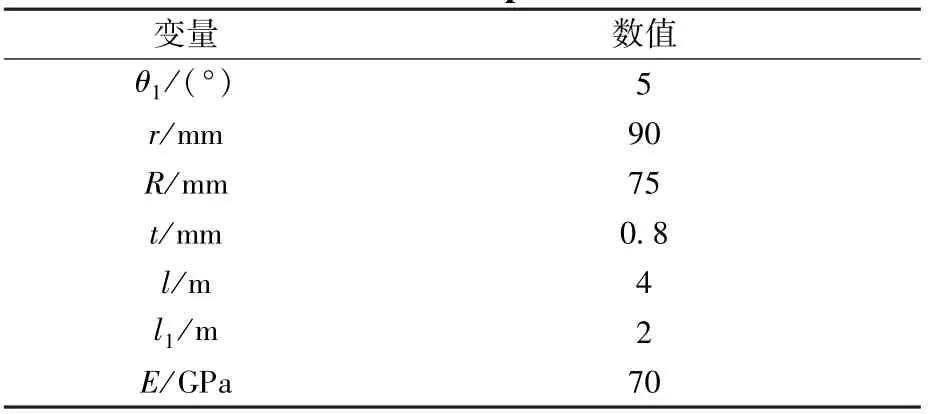
表1 伸展臂参数Table 1 Boom parameters

3.2 伸展臂收拢过程应变能仿真分析

基于ABAQUS 有限元软件建模对应变能解析计算结果进行验证。 根据文献[7]，伸展臂宜采用S4R 壳单元进行计算。 杆壁采用各向同性材料(材料属性来自高强度合金钢：弹性模量E ＝70 GPa，泊松比ν＝0.3，厚度t ＝0.8 mm)，摩擦因数μ＝0.15；取卷轴为离散刚体材料。 综合考虑计算量、收敛性等方面要求，伸展臂及卷轴均采用四边形网格，网格大小为30 mm；模型中杆壁自身的接触定义为通用接触，其它接触均定义为面-面接触以提高计算精度。 取表1 中尺寸参数在ABAQUS 软件中建立有限元模型如图5 所示。 伸展臂展平及卷绕过程分为3 步(图6)：①在伸展臂端部开口处向两侧分别施加大小相同的载荷，使伸展臂端部逐渐展开；②在端部施加垂直于壳表面的载荷P，使伸展臂端部压紧在卷轴上，并将端部固定于卷轴；③释放前两步中施加的载荷，同时施加角位移使卷轴滚动，伸展臂逐渐展平并卷绕在卷轴上。 因伸展臂展收速度较慢，根据文献[8]可将其运动过程视为准静态过程，应用静力法分析计算。

图5 伸展臂有限元模型Fig.5 Finite element model of boom

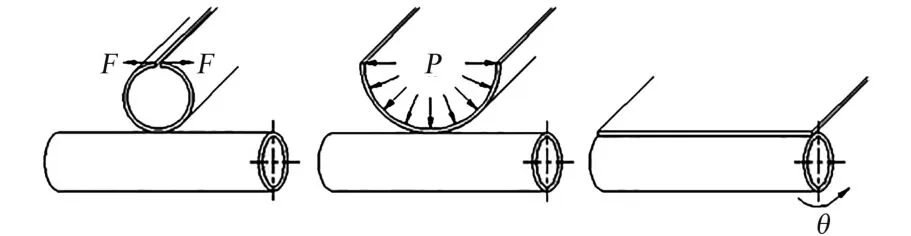
图6 伸展臂有限元模型卷绕过程Fig.6 Coiling process of boom finite element model

通过对ABAQUS 有限元模型进行分析得到伸展臂过渡段应变能Et＝84.75 J，总应变能Es随收拢长度l1的变化趋势与3.1 节MATLAB 计算结果对比如图7 所示，伪应变能、摩擦耗能如对比图8 所示。

图7 伸展臂收拢过程总应变能Fig.7 Total strain energy of boom during coiling

由图7 可知，伸展臂收拢过程中总应变能线性增大。 通过对比两条曲线可知，计算结果与仿真结果吻合的较好。 由图8 可知，收拢过程中摩擦耗能逐圈增大，伪应变能线性增大，但二者均保持在总应变能的1%以内，因此对整体模型计算的影响可忽略。

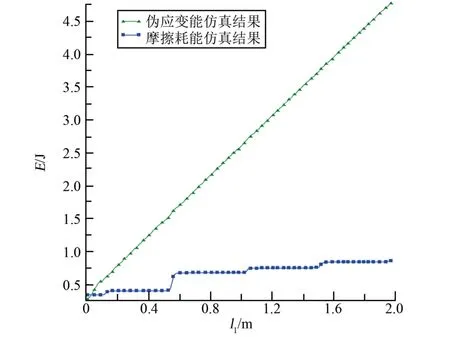
图8 伸展臂收拢过程伪应变能、摩擦耗能Fig.8 Pseudo strain energy and friction energy consumption in the process of boom coiling

3.3 伸展臂收拢过程应变能参数分析

因过渡段应变能Et在总应变能Es中所占比例不大且几乎恒定，此处仅研究收拢段应变能Ew随参数的变化规律。 取尺寸参数t(伸展臂厚度)、θ1(半开口角度)、R(卷轴外半径)及r(伸展臂外半径)，在表1 所列数值中上下各浮动50%，通过MATLAB 程序进一步分析各尺寸参数改变对收拢段应变能Ew的影响程度。 图9 所示为收拢段应变能Ew随参数t、θ1的变化关系，收拢段应变能Ew随参数r、R 的变化关系如图10 所示。

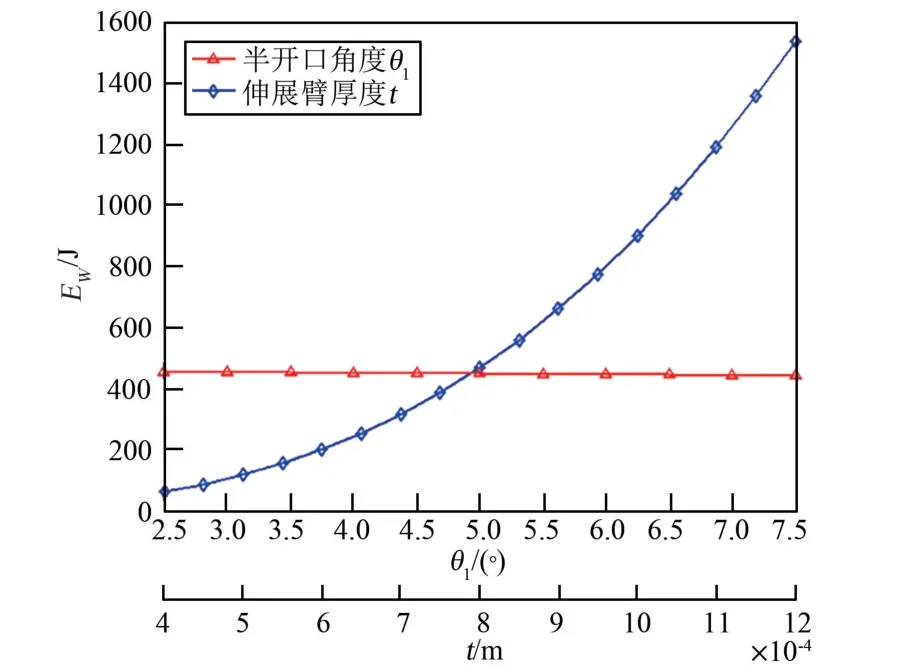
图9 伸展臂参数t、θ1 与收拢段应变能关系Fig.9 Relationship between boom parameters t， θ1 and the strain energy during coiling

由图9 可知，收拢段应变能Ew随伸展臂厚度t 的增大而增大，在同样浮动50%的情况下，t 的改变对总应变能影响最为明显，而θ1的改变影响最微小。

图10 伸展臂参数r、R 与收拢段应变能关系Fig.10 Relationship between boom parameters r，Rand strain energy during coiling

由图10 可知，收拢段应变能Ew随卷轴外半径R 的增大而减小(因曲率半径减小)，影响程度较为明显。 伸展臂外半径r 的影响规律较为复杂：当R 较小时收拢段应变能Ew随r 的增大而非线性增大，当R 较大时收拢段应变能Ew随r 的增大而非线性减小，当R 位于中间部分时收拢段应变能Ew在80 mm 附近出现了极小值。 这是由于r 的增大一方面减小了伸展臂展平过程的初始曲率，另一方面却增大了伸展臂横截面的周长，二者综合作用的结果。

4 伸展臂展开驱动力矩分析

由于伸展臂收拢过程中摩擦耗能很小(图8)，故可认为收拢过程中的阻力矩等于展开过程中的驱动力矩。

4.1 伸展臂展开驱动力矩计算分析

在伸展臂展开过程中，截面微元由卷绕状态至完全展平、由完全展平至自由状态的2 个过程依次独立发生，相互作用很小，同时展开驱动力矩主要有前一过程提供，因此忽略后一过程的影响。 当伸展臂收拢至a1角时，伸展臂阻力矩M 为式(11)：

取表1 中参数，通过MATLAB 编程计算，得到已卷绕长度l1从0 变化至2 m 过程中阻力矩M随l1变化过程的计算结果，如图11 所示。

由图11 可知，阻力矩M 随着卷绕长度的增大而线性地减小，这是由于随着卷绕长度的增加卷绕半径不断增大，导致卷绕部分曲率半径κa1不断减小。 但该因素影响程度很不明显，不及1%。

4.2 伸展臂展开驱动力矩仿真分析

图11 伸展臂收拢过程力矩对比Fig.11 Comparison of torque during boom coiling process

通过对ABAQUS 有限元模型进行分析得到伸展臂收拢过程中的阻力矩，如图11 所示，阻力矩总体上随卷绕过程的进行而减小，但每一周内有明显波动，尤其在每周起始处。 这是由于卷绕曲线并非理想中半径均匀增大的阿基米德螺旋线，而是在每一周的起始处突然递增，从而产生了阻力矩的突变。

对比图11 中仿真结果与计算结果，仿真值较计算值减小速率更大，这是由于仿真卷绕过程中不紧密卷绕导致曲率半径增大更快，如图12 所示，同时每周内阻力矩的波动也缘于此不紧密卷绕。 阻力矩仿真值较计算略大，这是由于伸展臂由完全展平至自由状态的过程对力矩也有略微影响。

图12 仿真过程中不紧密卷绕现象Fig.12 Non-tightly coiling during simulation

4.3 伸展臂展开驱动力矩参数分析

取尺寸参数t(伸展臂厚度)、θ1(半开口角度)、R(卷轴外半径)及r(伸展臂外半径)，在表1所列数值中上下各浮动50%，通过MATLAB 程序进一步分析各尺寸参数改变对阻力矩的影响程度。 图13 所示为阻力矩随参数t、θ1的变化关系。 阻力矩随参数r、R 的变化关系如图14 所示。

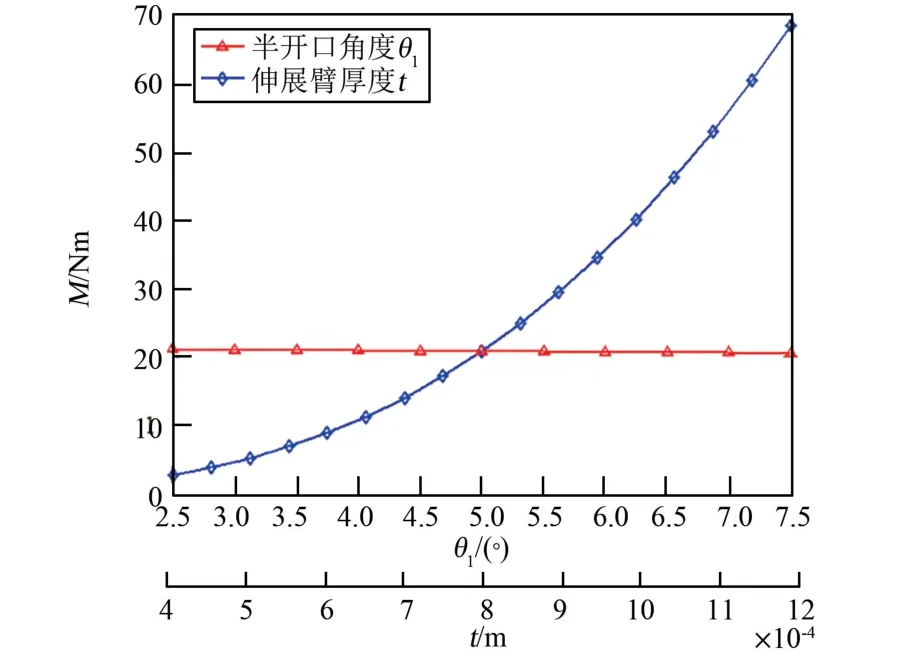
图13 伸展臂参数t 与驱动力矩关系Fig.13 Relationship between parameter tand driving torque

图14 伸展臂参数r、R 与力矩关系Fig.14 Relationship between parameters r， R and driving torque

由图13 可知，阻力矩随伸展臂厚度t 的增大而增大，在同样浮动50%的情况下，t 的改变对阻力矩影响最为明显，而θ1的改变影响最微小。

由图14 可知，阻力矩随卷轴外半径R 的增大而减小(因卷绕曲率降低)，随伸展臂外半径r 的增大而线性增大(因伸展臂横截面周长增加)，二者影响程度均比较明显。

5 伸展臂收拢过程应力分析

通过分析伸展臂卷绕过程中的应力分布及变化规律能够得到杆壁最易失效点从而指导设计。分析伸展臂卷绕状态下的应力应首先分析沿伸展臂纵截面方向的应力分布。 自中心对称面向外，在伸展臂的0、1/2、1 处依次选取内截面、中截面、外截面，如图15 所示。

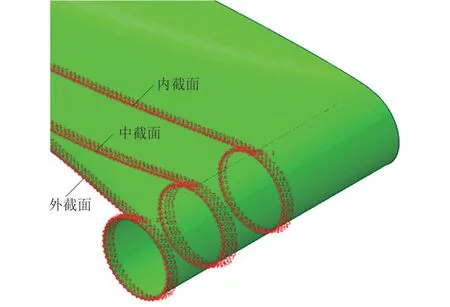
图15 伸展臂纵截面示意图Fig.15 Diagram of longitudinal-section of boom

应用第四强度理论，通过ABAQUS 软件绘制伸展臂Von Mises 等效应力云图。 由于伸展臂过渡段及自由段应力较低且变化均匀，因此仅从展平端开始取1 m 范围进行分析，如图16 所示。 图中x 轴为纵截面内沿管壁的实际尺寸位移(m)，方向为自展平端至自由端，y 轴为Von Mises 等效应力(Pa)。

图16 伸展臂纵截面Von Mises 等效应力分布Fig.16 Von Mises stress distribution in longitudinalsection of boom

由图16 可知，伸展臂在由自由弯曲状态转化为卷绕弯曲状态的过渡区域内，以及在伸展臂端部附近一定区域内出现了等效应力突变及最大值，而在伸展臂其它区域中等效应力变化比较平缓。 因此在伸展臂过渡区域及伸展臂端部附近易因畸变能密度过大而产生屈服失效。

通过观察伸展臂转绕过程中各处应力值可知，伸展臂收拢过程中最大等效应力点始终位于伸展臂端部。 收拢第一周内该点于端部截面上(位置不固定)，收拢一周后该点始终位于端部横截面中心处，如图17 所示。

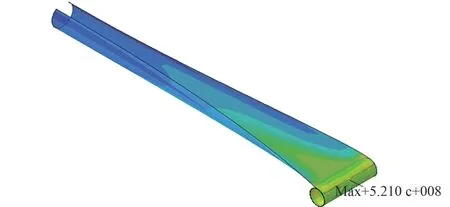
图17 伸展臂最大Von Mises 等效应力点Fig.17 Maximum Von Mises stress point in boom

根据上述分析，取卷轴分别转动至1 周、2 周及3 周处，伸展臂端部横截面上各处等效应力值并绘制曲线，如图18 所示。 图中横轴为横截面内沿管壁实际尺寸(m)，纵轴为Von Mises 等效应力(Pa)。

图18 伸展臂端部等效应力分布Fig.18 Von Mises stress distribution in boom tip

由图18 可知，在卷绕一周后中心处的等效应力为最大应力点，并随着卷绕的进行不断增高。因此该点为伸展臂上最易失效点，根据第四强度理论，此处易因畸变能密度过大而产生屈服失效。

高强度合金钢许用应力为σ＝700 MPa，图17中应力低于许用应力，复合材料设计要求。 根据图9，当壁厚为0.9 mm 时等效应力将大于许用应力，因此对于该尺寸的伸展臂，其设计厚度t 应小于0.9 mm。 另外，实际设计中应考虑安全裕度等问题预留出更大的安全空间。

6 结论

1)薄壁圆管开口式伸展臂总应变能受到伸展臂厚度t 改变的影响最明显，半开口角度θ1的改变影响最微小，卷轴外半径R 的影响程度适中。 伸展臂外半径r 对总应变能的影响与R 有关：R 较小时r 曲线单调，R 较大时r 曲线出现了极小值。

2)驱动力矩受到伸展臂厚度t 改变的的影响最为明显，半开口角度θ1的改变影响最微小，卷轴外半径R 的及伸展臂外半径r 的影响程度适中。

3)伸展臂在由自由弯曲向卷绕弯曲过渡的区域内及展平端附近等效应力发生了突变，因此在该区域内易发生失效。 卷绕过程中最大等效应力点始终位于伸展臂端部，收拢一周后该点始终位于端部横截面中心处，其等效应力值随着卷绕的进行不断增高。 该点为伸展臂上最易失效点。

参考文献(References）

[ 1] Johnson L， Whorton M， Heaton A， et al. Nano sail-D： A solar sail demonstration mission[J]. Acta Astronaut， 2011，68(5-6)： 571-575.

[ 2] Chung P， Thornton E. Torsional buckling and vibrations of a flexible rolled-up solar array[C]/ /36thStructures， Structural Dynamics and Materials Conference. New Orleans， LA， U.S.A： AIAA， 1995： 1355.

[ 3] Pleelgrino S. Large retractable appendages in spacecraft[J].Journal of Spacecraft and Rockets，1995，32(6)：1006-1014.

[ 4] Ross B， Woo N， Blandino J R. Simulation of the deployment of a flexible roll-up solar array using multi-body dynamics software[C]/ /3rdAIAA Spacecraft Structures Conference.San Diego， California， USA： AIAA， 2016： 1703.

[ 5] Chu Z Y， Lei Y A. Design theory and dynamic analysis of a deployable boom[J]. Mechanism and Machine Theory，2014，71： 126-141.

[ 6] 张展智， 赵国伟， 焦景勇， 等. 空间薄壁式伸展臂的展开仿真与卷绕方式研究[J]. 宇航学报， 2013， 34(3)： 299-307.

Zhang Z Z， Zhao G W， Jiao J Y， et al. Research on the deployment simulation and curling mode of space thin-walled extension arm[J]. Acta Astronautica Sinica， 2013， 34 (3)：299-307.(in Chinese)

[ 7] 李瑞雄， 陈务军， 付功义， 等. 透镜式缠绕肋压扁缠绕过程数值模拟分析[J]. 宇航学报， 2011， 32(1)： 224-232.

Li R X， Chen W J， Fu G Y， et al. Numerical simulation analysis of flattening and winding process of lens type winding rib[J]. Acta Astronautica Sinica， 2011， 32 (1)： 224-232.(in Chinese)

[ 8] 李瑞雄， 陈务军， 付功义，等. 透镜式缠绕肋压扁缠绕过程静力法与动力法数值模拟分析研究[C]/ /第十届全国现代结构工程学术讨论会， 天津， 2010.

Li R X， Chen W J， Fu G Y，etal. Study on numerical simulation of static and dynamic methods in the process of flattening and winding of lens type winding rib[C]/ /The 10thNational Symposium on modern structural engineering， Tianjin， 2010.(in Chinese)

[ 9] 邹涛， 陈务军， 彭福军， 等. 透镜式缠绕肋收展过程数值模拟分析[J]. 哈尔滨工程大学学报， 2013 34(2)： 151-156.

Zou T， Chen W J， Peng F J， et al. Numerical simulation analysis of the unfolding and retracting process of lens wound rib[J]. Journal of Harbin Engineering University， 2013， 34(2)： 151-156.(in Chinese)

[10] 蔡祈耀， 陈务军， 张大旭， 等. 透镜式薄壁管状空间伸展臂压扁拉扁数值模拟与试验[J]. 上海交通大学学报，2016， 50(04)： 601-607.

Cai Q Y， Chen W J， Zhang D X， et al. Numerical simulation and experiment of flattening and flattening of lens thin-walled tubular space extension arm [J]. Journal of Shanghai Jiaotong University， 2016， 50(04)： 601-607.(in Chinese)