航天器点阵夹层圆柱壳构型多学科优化设计

许 琦，阎 军*，蒋存存，范志瑞，郝 平，周 强，郭军辉，孙 维

(1. 大连理工大学工业装备结构分析国家重点实验室，大连116024； 2. 北京空间技术研制试验中心，北京100094)

1 引言

随着我国载人航天事业的快速发展，深空探测成为我国航天领域不可或缺的一环[1]。 深空探测存在周期长、距离远以及宇宙环境复杂等诸多因素，在复杂环境下，航天器结构能否满足承载、隔热、防撞击等方面性能，直接影响任务执行的成败。 深空探测航天器结构需满足多学科、多功能、多系统协同工作的设计要求，而传统的铝合金加筋壳结构功能单一，已经不能满足航天探测任务的需求。 为此，设计一种集承载、隔热、防撞击等性能于一体的多功能融合圆柱壳结构是解决目前深空探测领域瓶颈问题的方案之一。

三维点阵结构被认为是最具潜力的下一代轻量化多功能结构形式之一，点阵材料作为一种结构化材料，有着传统金属或合金材料所不具备的力学及物理性能，如超轻质、高比刚度、高比强度、多功能化以及性能可设计性等优势[2]，工程中常用的点阵结构拓扑构型包括四面体型[3]、金字塔型[4]、Kagome 型单胞[5]，这些构型已成功应用于航空航天领域，如火箭承力筒、航天器机身、级间段、直升机尾翼等[6]。

目前，针对点阵结构的研究多集中在点阵结构的力学、热学等物理性能方面，通过对比不同单胞构型结构在实际工况中的使用情况，研究其结构及物理属性[7-8]。 基于点阵结构的特点，其构成的材料多用于吸能设计，张国旗[9]基于金字塔形单胞构成的夹芯板，研究了复合材料点阵结构的吸能及低速冲击性能；杨辉等[10]对金属点阵结构的低速冲击性能进行了分析；郑华勇[11]建立了理想冲击载荷下的3D-Kagome 点阵夹层板等效刚度和强度的分析方法，且以结构抗冲击性能为目标，进行了数值优化设计，发现3D-Kagome 点阵夹芯板在抗冲击性能方面具有很大的优势；Wadley[12]针对多空的金属结构制造进行了研究；赵冰等[13]研究了基于钛合金的金字塔型、四面体型、X型等三维点阵结构的制备工艺与压缩性能，分析了不同单胞构型在弹性变形、弹性屈曲等方面的性能优势。 上述研究多是基于某一具体单胞构型构成的宏观结构进行的力学性能分析，但针对宏观结构的优化设计，研究还不够充分。 工程实际往往涉及热、力等多学科响应，且学科间有着一定的相互作用，采用单目标进行结构优化设计显然不能满足实际工程需求。

现有多目标的优化多采用Isight 软件设计，实验设计及代理模型技术的引入在很大程度上降低了多学科优化中的大规模有限元计算。 基于Isight 软件进行优化的流程为：首先进行单胞选型设计和样本点数据构造，然后通过Abaqus 参数化建模得到样本点数据在外载荷下的强度、屈曲荷载等响应，最后在此基础上构造代理模型并进行多目标优化。 俞必强等[14]基于Isight 优化平台提出了多学科随机搜索优化算法，克服了传统解耦方法的局限性。 赵国伟等[15]基于Isight 和ABAQUS 对制动蹄进行轻量化设计，优化结果实现了轻量化，同时保证了强度和刚度满足设计需求。

综上所述，本文基于四面体单胞构型，建立双层点阵圆柱壳，基于单目标优化及不同宏观密度，考察结构的整体强度性能和抗屈曲性能，探究影响结构性能的因素。 以结构的总质量、等效热传导系数、一阶屈曲载荷为目标进行了多目标优化设计，考虑制造性约束，根据优化算法给出多目标优化中Pareto 解集中的前沿解，作为最终点阵圆柱壳结构设计的参考。

2 航天器设计要求及有限元模型建立

2.1 技术指标

航天器为航天员提供了基本的生存环境，其承载、密封、空间辐射屏蔽等综合性能决定了航天员安全及生理、心理健康。 结合工程实际，在轻量化设计的同时，航天器所考虑的工况及相应的设计需求如下：

1)采用总高度为6.4 m 的双层四面体夹层点阵圆柱壳舱壁结构(图1)，其总质量M≤1129 kg；

2)发射过程中，航天器纵向超重加速度为6.8g，横向超重加速度为0.5g，舱壁结构的一阶屈曲载荷Fb＞2000 kN；

3)在稳态条件下对点阵圆柱壳结构进行热传导设计，结构的等效热传导系数κ＜2.5 W/(m·K)；

4)在轨运行时，舱体内部承受0.15 MPa 的气压，其最大Mises 应力σmax＜300 MPa。

图1 双层四面体夹层点阵圆柱壳舱壁结构示意图Fig.1 Schematic diagram of double tetrahedral sandwich lattice cylindrical shell bulkhead structure

结构外表面直径Φ＝4000 mm、高度H＝6400 mm。根据实际运载火箭空间及舱内空间布置限制，舱壁结构的内外面板间距h ＝50～100 mm，外面板厚度t1＝0.5～2 mm，内面板厚度t2＝2～5 mm，中间面板厚度t0＝0.5～2 mm， 外层单胞杆件半径r1＝0.25～0.75 mm，内芯杆件半径r2＝1.25 ～1.75 mm，外层单胞高度h1＝20 ～40 mm。 结构整体采用7075 铝合金材料，其弹性模量E ＝71 GPa，泊松比γ ＝0.33，密 度ρ ＝2.81 g/cm3，热 传 导 系 数α ＝173 W/(m·K)，比热容c＝0.96 J/(g·K)。

2.2 有限元模型的建立

本文中需要建立不同单胞数目的点阵圆柱壳模型，内、外壳之间分布着大量杆件，且要求单胞内的杆件和内、外层壳面连接到一起，这样形成了具有大量周期性分布的微单胞结构，如果采用传统CAE 界面进行建模，重复工作量巨大，且每修改一次参数都需要重新操作一遍，并不现实。 因此基于Abaqus/Python 二次开发建立了不同单胞构型的点阵圆柱壳结构有限元模型，并进行静力分析和屈曲分析。 分析过程中，夹芯杆件采用空间二节点线性梁单元(B31)，内外壳采用空间四节点Mindlin 壳单元(S4R)。 网格划分过程中注意点阵结构与壳单元之间的连接需保证单元节点间距在容差范围之内，避免由于网格合并带来的有限元求解错误。 边界条件需对点阵圆柱壳结构下边界施加固支边界条件，并在内壳的内表面上施加一个大气压的压强，在上边界施加等效后的由内压产生的对壳体两端的拉力。 对于结构屈曲载荷分析而言，除上述内压作用下的载荷外，还需对全部壳单元施加重力相关体载荷，对全部梁单元施加重力等效后的线载荷。

3 点阵圆柱壳多学科优化过程

优化过程采用Isight 平台集成，使用多岛遗传算法[16]和NSGA-Ⅱ算法[17]进行求解。 同时，为了克服优化迭代中有限元计算所带来的大量计算成本，优化引入了代理模型技术。 常用的代理模型创建方法包括响应面法、Kriging法及径向基函数法等。 响应面法对非线性程度较高的模型拟合精度较差，Kriging 模型需要大量的采样点。 考虑到屈曲特征值等目标或约束与设计变量之间的强非线性函数关系，本文采用径向基函数创建代理模型，可对高度非线性模型有很好的近似，且所需样本点数目较少[18]，其数学表达式如式(1)所示：

其 中， w(x) ＝[w1…wn]T，φ ＝[φ(d1)…φ(dn)]T，wi是权系数， φ(di) 是径向函数， di＝‖x - xi‖ 是待测点x 与样本点xi之间的欧氏距离。

采用Isight 软件的优化流程图如图2 所示，具体步骤如下：

图2 点阵圆柱壳多学科优化流程图Fig.2 Flowchart of multi-disciplinary optimization of cylindrical shell lattice structure

1)在给定变量的取值范围内，采用拉丁超立方采样方法生成变量空间内均匀的样本点。

2)根据各样本点设计参数的取值，采用Abaqus 参数化建模技术，建立航天器舱壁有限元模型。 通过有限元分析，求得结构的热学、力学响应，即内压作用下结构强度指标、等效热传导系数、结构极限屈曲载荷。

3)以航天器结构的舱壁厚度与杆件半径等作为输入变量，将结构内压作用下的强度与热传导系数等作为输出变量，建立设计变量与结构响应之间的径向基神经网络代理模型。采用交叉验证技术[19]，验证所建立的代理模型精度。 在验证过程中，将样本数据分成训练集和测试集2 个互补的子集。 为了降低结果的可变性，通常对一个样本数据集进行多次不同的划分，得到不同的互补子集，进行多次交叉验证，并取多次验证的平均值作为验证结果。如果精度不满足要求，则重复步骤1) ～3)，直至满足要求为止。

4)获取满足精度要求的代理模型后，采用适当的优化算法对航天器进行单目标(多岛遗传算法)/多目标(NSGA-II 算法)的优化。

4 单目标优化设计

根据2.1 节航天器的设计要求，舱壁采用双层四面体点阵夹层圆柱壳结构。 由于3D 打印的制造性约束要求，单胞的杆件半径和单胞高度存在约束关系：hi≪40×ri＋10。 以点阵夹层圆柱壳总质量M 为目标函数，考虑结构的热传导系数、强度、极限屈曲载荷为约束条件，其优化列式见式(2)。 其中，X 为设计变量的集合，各变量的含义详见2.1 节。

分别研究不同周向、径向单胞数目对结构物理性能的影响。

4.1 设计1：周向单胞30 个，径向单胞4 个

双层点阵夹层圆柱壳结构采用周向单胞数目为30 个，径向单胞数目为4 个的排布方案。 优化过程中，热传导系数采用热阻模型[20]计算得到，最大Mises 应力以及一阶极限屈曲载荷通过Abaqus 有限元分析得到，为降低优化的成本，采用代理模型建立了目标函数M 和设计变量之间的映射关系。 在径向基代理模型创建过程中，采用最优拉丁超立方法[21]生成1000 个分布均匀的样本点，并计算各样本点所对应的最大Mises 应力和一阶屈曲载荷。

采用多岛遗传算法进行单目标优化，种群数目为100，岛数量为5，最大代数为200，交叉与变异概率均为0.05，优化结果见表1。 通过Abaqus对优化结果进行校核，得到结构最大Mises 应力为127.9 MPa，一阶屈曲特征值λb为1201，一阶屈曲载荷Fb为1.2×107N，满足设计约束，得到应力云图和结构一阶屈曲模态见图3。

图3 设计1 单目标优化结果校验Fig.3 Validation of the single-objective optimized results of the first design

4.2 设计2：周向单胞45 个，径向单胞4 个

采用与设计1 相同的模型参数，加密周向单胞数到45 个，径向单胞数仍为4 个，以结构最小总质量为目标进行单目标优化设计。 优化结果见表1，通过Abaqus 对优化结果进行校核，得到结构最大Mises 应力为156.1 MPa，一阶屈曲特征值为549，一阶极限屈曲载荷Fb为4.2×106N，应力云图和一阶屈曲模态见图4。

图4 方案2 单目标优化结果校验Fig.4 Validation of the single-objective optimized results of the second design

4.3 设计3：周向单胞360 个，径向单胞4 个

进一步加密周向单胞数到360 个，径向单胞数为4 个，其余参数不变，以结构最小总质量为目标函数进行单目标优化，优化结果见表1。 通过Abaqus 对优化结果进行校核，得到结构最大Mises 应力为156.2 MPa，一阶屈曲特征值为481，一阶极限屈曲载荷Fb为6.2×106N，应力云图和一阶屈曲模态见图5。

从上述3 种设计结果中可知，两层点阵夹层圆柱壳既能满足对结构强度、抗屈曲性能的要求，同时单位长度的结构总质量更小，且四面体单胞易于制造，符合设计需求。 随着单胞密度的增加，最为敏感的是结构的热传导系数，结构越密，隔热性能越差。 单胞数为30 和45 时，杆件尺寸较大，适合采用传统工艺方法制造，当采用3D 打印技术进行制造时，对单胞内杆件的倾斜角度有要求，周向单胞数为360 个的设计方案更符合3D 打印中对悬垂角的要求。

图5 方案3 单目标优化结果校验Fig.5 Validation of the single-objective optimized results of the third design

5 多目标优化设计

由于点阵夹层圆柱壳结构多应用于多种物理场共同作用的环境，对该结构进行多目标优化设计，采用和单目标优化过程中相同的结构，几何参数不变，单胞阵列数目采用4.3 节讨论的满足制造约束要求的单胞排列数目，即周向360 个，径向4 个。 结构物理参数与单目标优化采用的参数一致。 此处采用NSGA 多目标优化算法对结构整体热传导、强度指标进行多目标优化设计，通过多次试算调整，设置种群规模为100，最大迭代数目为200，变异率为0.2，交叉率为0.9。 优化列式如式(3)所示：

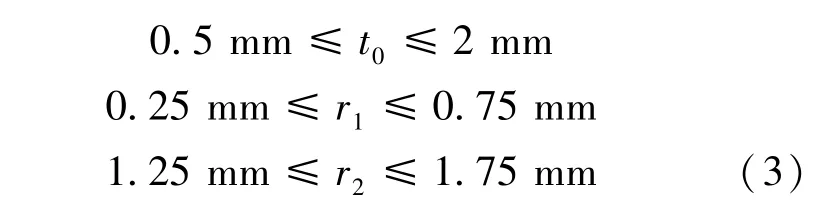
基于目前已经获得的双层点阵圆柱壳结构的多学科优化结果，给出以质量、热传导系数以及Mises 应力为目标的Pareto 解集，并将Pareto 解集在每2 个目标函数所构成的平面内投影，如图6所示。 图6 反映了在给定约束下，最优设计方案中各目标函数取值界限及其相互影响关系。 当满足轻量化需求时，可使得结构的热传导系数下降，但同时使得结构的Mises 应力提升，结构强度失效的风险增加。 因此考虑设计中的不同需求，在满足强度、轻量化和热传导系数的前提下，从Pareto 解集中获得几组多目标优化的代表性解，分别用于描述多功能结构的最小应力、最小传热性能和最小质量，如表2 所示。 在以最小应力为指标的代表性解中，各设计变量的取值均比较大，这有利于增加结构整体的刚度，降低应变水平，从而使得应力最小。 在以最小质量为指标的代表性解中，内外层及中间层壳体的厚度均比较小，由于壳体质量在总质量中占主导，降低壳体厚度可有效降低结构质量。 由于优化中引入了最大应力约束，因此为了降低应力水平，杆件的尺寸相应增大。 然而，杆件尺寸的增大增加了点阵夹层的有效传热面积，热传导系数也相应增大。 当以最小传热为指标的代表性解中，杆件的面积均较小。为了避免由于杆件面积变小而引起的应力过大，三层壳体的厚度均得到加强，通过减小杆件应变以达到降低应力水平的目的。

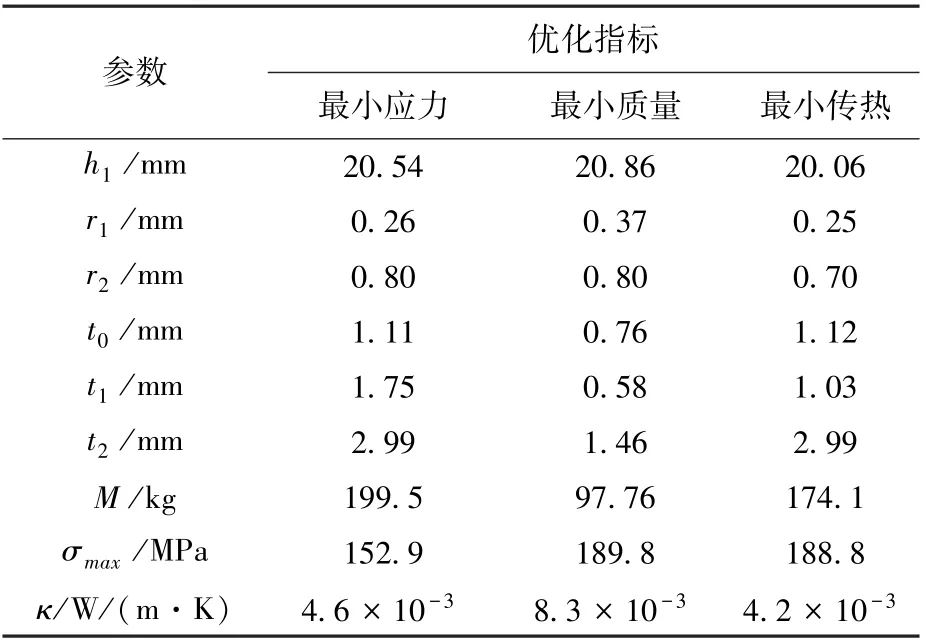
表2 多目标优化代表性解Table 2 The representative solution of multi-objective optimization

图6 多目标优化的Pareto 解集Fig.6 The Pareto set of multi-objective optimization

6 结论

1)通过对四面体夹层点阵圆柱壳结构进行单目标优化可知，单胞密度对结构的热传导系数影响较大，单胞密度越大，结构的隔热性能越差。此外，单胞密度的增加会对结构的最大Mises 应力造成影响。

2)双层点阵圆柱壳既能满足对结构强度、抗屈曲性能的要求，同时单位长度的结构总质量最小，而且由于四面体单胞制造更方便，因此在满足设计要求的同时更适合在实际的工程应用。

3)基于双层四面体点阵结构的多目标优化，给出了多物理场情况下，分别用于描述多功能结构的最小应力、最小传热性能和最小质量的最优解集，为实际工程中点阵圆柱壳的应用提供了理论基础与优化设计方面的指导。

参考文献(References）

[ 1] 李一帆. 载人深空探测关键技术研究[J]. 导弹与航天运载技术， 2018 (1)： 24-31.

Li Y F. Research on the key technologies in manned deep space exploration[J]. Missiles and Space Vehicles. 2018(1)： 24-31.(in Chinese)

[ 2] Evans A G，Hutchinson J W，Fleck N A，et al. The topological design of multifunctional cellular metals[J]. Progress in Materials Science， 2001， 46(3-4)：309-327.

[ 3] Deshpande V S， Fleck N A. Collapse of truss core sandwich beams in 3-point bending[J]. International Journal of Solids and Structures， 2001， 38(36-37)：6275-6305.

[ 4] Wallach J C， Gibson L J. Mechanical behavior of a three-dimensional truss material[J]. International Journal of Solids and Structures， 2001， 38(40-41)：7181-7196.

[ 5] Hyun S， Karlsson A M， Torquato S， et al. Simulated properties of Kagomé and tetragonal truss core panels[J]. International Journal of Solids ＆ Structures， 2003， 40(25)：6989-6998.

[ 6] Del Olmo E， Grande E， Samartin C R， et al. Lattice structures for aerospace applications[J]. European Space Agency，2012， 691： 6.

[ 7] 王展光， 刘利军，应建中，等.金字塔形栅格材料的静态压缩力学性能[J].热加工工艺，2011，40(10)：27-29.

Wang Z G，Liu L J， Ying J Z， et al. Static compressive properties of pyramidal lattice material[J]. Material ＆ Heat Treatment， 2011，40(10)：27-29.(in Chinese)

[ 8] 张弥，王晓东，苏亚东，等.钛合金点阵夹芯结构弯曲性能[J].中国有色金属学报，2018，28(03)：457-464.

Zhang M，Wang X D，Su Y D，et al. Bending behavior of titanium truss core sandwich structure[J]. The Chinese Journal of Nonferrous Metals， 2018，28(03)：457-464.(in Chinese)

[ 9] 张国旗. 复合材料点阵结构吸能特性和抗低速冲击性能研究[D]. 哈尔滨：哈尔滨工业大学，2014.

Zhang G Q. Energy Absorption and Low Velocity Impact Damage Desistance of Composite Lattice Structure[D]. Harbin：Harbin Institute of Technology， 2014.(in Chinese)

[10] 杨辉，尹冠生，李轩，等.金属点阵格栅三明治结构低速冲击响应分析[J].塑性工程学报，2018，25(04)：245-253.

Yang H， Yin G S， Li X， et al. Analysis on response of metal lattice sandwich structures under low velocity impact[J].Journal of Plasticity Engineering，2018，25(04)：245-253.(in Chinese)

[11] 郑华勇. 3D-Kagome 点阵夹芯板的力学性能研究[D]. 哈尔滨：哈尔滨工业大学， 2006.

Zheng H Y. Mechanical Performance of the 3D Kagome Truss Panels[D]. Harbin： Harbin Institute of Technology， 2006.(in Chinese)

[12] Wadley H N G. Cellular metals manufacturing[J]. Advanced Engineering Materials， 2002， 4(10)：726-733.

[13] 赵冰，李志强，侯红亮，等.钛合金三维点阵结构制备工艺与压缩性能研究[J].稀有金属，2017，41(03)：258-266.

Zhao B，Li Z Q，Hou H L，et al. Fabrication and compression test of titanium alloy with three dimensional lattice structure[J]. Chinese Journal of Rare Metals， 2017， 41(03)：258-266.(in Chinese)

[14] 俞必强，杨晓楠，李威.基于Isight 的多学科随机搜索优化方法[J].计算机集成制造系统，2019，25(03)：743-751.

Yu B Q，Yang X N，Li W. Multidisciplinary stochastic search optimization method based on Isight[J]. Computer Integrated Manufacturing Systems，2019，25(03)：743-751.(in Chinese)

[15] 赵国伟，唐进元，张质子.ISIGHT 集成CATIA 和ABAQUS的制动蹄轻量化设计[J].中南大学学报(自然科学版)，2016，47(07)：2260-2265.

Zhao G W， Tang J Y， Zhang Z Z. Brake shoe’s lightweight design based on ISIGHT integrated CATIA and ABAQUS[J].Journal of Central South University，2016，47(07)：2260-2265.(in Chinese)

[16] Whitley D， Rana S， Heckendorn R B. The island model genetic algorithm： On separability， population size and convergence[J]. Journal of Computing and Information Technology，1999， 7(1)： 33-47.

[17] Deb K，Pratap A，Agarwal S，et al. A fast and elitist multiobjective genetic algorithm： NSGA-II[J]. IEEE Transactions on Evolutionary Computation， 2002， 6(2)： 182-197.

[18] 刘哲， 金达锋， 范志瑞. 基于代理模型的复合材料带加强筋板铺层优化[J]. 清华大学学报：自然科学版， 2015(7)：782-789.

Liu Z， Jin D F， Fan Z R. Laminate optimization of a composite stiffened panel based on surrogate model[J]. Journal of Tsinghua University(Science and Technology)， 2015(7)：782-789.(in Chinese)

[19] Krogh A， Vedelsby J. Neural network ensembles， cross validation， and active learning[C]/ /Advances in Neural Information Processing Systems 7，MIT Press， 1995： 231-238.

[20] 李嘉禄，高涵，焦亚男. 基于热阻网格法的正交三向复合材料导热系数预测模型[J]. 天津工业大学学报，2019，38(05)：20-24.

Li J L， Gao H， Jiao Y N. Thermal conductivity prediction model of orthogonal three-directional composites based on thermal resistance grid method[J]. Journal of Tianjin University of Technology，2019，38(05)：20-24.(in Chinese)

[21] Jin R， Chen W， Sudjianto A. An efficient algorithm for constructing optimal design of computer experiments[J]. Journal of Statistical Planning and Inference， 2005， 134(1)： 268-287.