基于Kriging 代理模型的大直径运载火箭蒙皮桁条结构分步优化方法研究

吴 栋，王志祥，刘观日，张大鹏*，雷勇军

(1. 国防科技大学空天科学学院，长沙410073； 2. 北京宇航系统工程研究所，北京100076)

1 引言

薄壁加筋圆柱壳结构是航空航天结构中常见的结构形式，蒙皮桁条结构是其中一种典型的结构。 现有运载火箭型号中约有80%的箭体舱段采用了整体加筋和桁条加强的薄壁壳体结构，如运载火箭的级间段蒙皮桁条和贮箱等结构[1-2]。针对蒙皮桁条结构开展优化设计能减轻运载火箭箭体的结构质量，并且对提升运载火箭的可靠性、安全性和发射成功率有着重要意义。

近年来，研究人员基于层级设计理念[1-3]开展了大量多级加筋结构承载能力和优化研究。Wang 等[4]提出了一种多级加筋板结构，并对该结构开展了轴压作用下极限承载能力和缺陷敏感性的研究；Wang 等[5]和郝鹏[6]提出了考虑初始几何缺陷的薄壁加筋圆柱壳结构在轴压作用下极限载荷的预测方法，并基于该方法提出了考虑几何缺陷的薄壁加筋圆柱壳结构的优化设计方法；范书群等[7]基于有限元方法，提出一种半硬壳结构框-桁匹配设计方法；张铁亮等[8]基于代理模型对加筋板的布局进行优化；张柱国等[9]基于进化Kriging 模型的优化方法对金属加筋板的尺寸和布局进行设计；郝鹏等[10]基于径向基函数代理模型，提出一种蒙皮桁条结构新型减轻孔设计。

10 m 级重型运载火箭对结构减重有较大的需求，同时尺度效应又增加了设计难度。 目前，针对10 m 级重型运载火箭薄壁加筋圆柱壳结构的轻质优化研究较少。 本文以10 m 级重型运载火箭的结构轻质优化设计为背景，以大直径运载火箭级间段蒙皮桁条结构为研究对象，基于Python语言建立蒙皮桁条结构参数化模型，采用显式非线性动力学算法分析结构的后屈曲状态，分析不同蒙皮网格规模对计算精度和计算效率的影响规律；针对蒙皮桁条结构优化中涉及连续的尺寸优化以及离散的拓扑优化问题，对优化变量进行合理分组，提出基于Kriging 代理模型和组合优化算法对蒙皮桁条结构进行分步优化，以获得不同截面形式桁条下的最优结构形式。

2 蒙皮桁条结构后屈曲分析

2.1 蒙皮桁条结构有限元建模

蒙皮桁条结构由蒙皮、桁条、中间框和端框组成。 蒙皮内侧沿着轴向均匀分布4 个“Π”型截面的中间框，2 个“L”型截面的端框。 蒙皮外侧沿着环向均匀分布若干根桁条，蒙皮桁条结构的几何模型如图1 所示，端框、中间框截面如图2 所示，桁条截面如图3 所示。

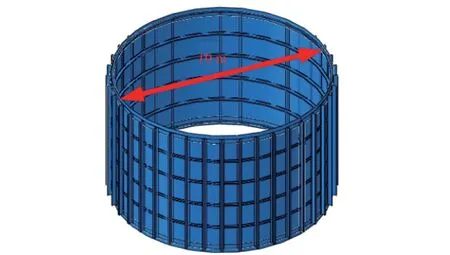
图1 蒙皮桁条结构几何示意图Fig.1 Geometric diagram of skinned truss structure

图2 端框和中间框截面示意图Fig.2 Schematic diagram of the end frame and the middle frame

图3 桁条截面示意图Fig.3 Schematic diagram of truss

基于Python 语言建立蒙皮桁条结构的参数化模型。 由于蒙皮桁条结构使用较薄的蒙皮和桁条，结构上体现为板壳特性，为了能够准确模拟桁条局部截面平动和转动，采用壳单元划分网格[11]，桁条腹板高度方向划分两层单元。 在蒙皮与桁条、蒙皮与端框、蒙皮与中间框之间施加粘接约束。 为获得轴压作用下蒙皮桁条结构的极限载荷，分别在上下端面建立参考点，并与相应端面节点建立多点耦合约束单元，对下参考点施加固支约束，上参考点约束除轴向位移外的其他自由度，匀速施加35 mm 强制位移。 模型选用铝合金材料，铝合金材料的弹性模量为70 GPa，泊松比为0.3，密度为2.78×10-6kg/mm3，屈服应力为440 MPa，强度极限为550 MPa，延伸率为6%。

2.2 蒙皮桁条结构后屈曲分析

对于轴压作用下的薄壁加筋圆柱壳结构，一般情况下，允许蒙皮在较小的载荷下发生局部失稳。结构的极限承载能力是由结构的后屈曲状态决定的，相较于弧长法和隐式非线性算法，显式非线性动力学算法能很好地跟踪轴压载荷下薄壁加筋圆柱壳结构的后屈曲行为[12]。 本文采用显式非线性动力学算法分析蒙皮桁条结构的后屈曲状态。

使用较粗的单元划分网格会使计算结果误差较大，较细的单元划分网格会导致结构分析计算量加大[13]，需要合理地设置网格规模。 为了准确反映蒙皮失稳模态，需分析蒙皮网格规模对显式非线性动力学算法的影响。 采用如表1 中所示的结构初始设计参数，得到3 种蒙皮网格规模对结构极限载荷的影响规律，如表2 所示。 随着蒙皮网格规模的提升，结构的极限载荷减少，表明网格的细化导致计算误差减小，计算精度提高，同时计算耗时相应增加。 筋格内网格数为4×23 与4×31相比，极限载荷计算结果相差0.56%，但计算耗时减少了1.3 倍。 综合考虑计算精度和计算效率，在后续计算中采用筋格内网格数量为4×23的蒙皮网格，如图4 所示。

表1 蒙皮桁条结构初始设计参数【注】Table 1 Initial design parameters of skinned truss structure

3 基于Kriging 代理模型和组合优化算法的分步优化策略

3.1 优化问题描述

蒙皮桁条结构的轻质优化包含拓扑优化、尺寸优化和几何优化[14]。 拓扑优化是优化桁条的数量；尺寸优化是优化单元的截面尺寸；几何优化是优化各结构的截面形状[14]，使其在满足承载能力需求的前提下通过改变截面形状提升结构的性能。 具体可以描述如式(1)所示：

其中，xHT为桁条参数， xHTmin为桁条各参数的下限，xHTmax为桁条各参数的上限；xZJK为中间框参数，xZJKmin为中间框各参数的下限， xZJKmax为中间框各参数的上限； xe＝0 表示“Π”型截面桁条，xe＝1 表示“I”型截面桁条，f(x) 为结构的质量表达式，Fcr为结构的极限载荷，Fcr*为结构的设计载荷。

3.2 Kriging 代理模型

在构建代理模型前，需选取样本点，通过后屈曲分析得到样本点的结构质量和极限载荷。 试验设计决定了构建代理模型的样本点规模和空间分布情况[9]。 本文采用试验设计中的优化拉丁超立方抽样方法选取样本点。 该方法具有良好的空间填充性和均匀性。 大多数试验设计方法中试验次数与因素个数成比例或指数增加，而优化拉丁超立方抽样方法的试验次数等于水平数，适用于影响因素较多的情况，能显著减少试验次数[9]。

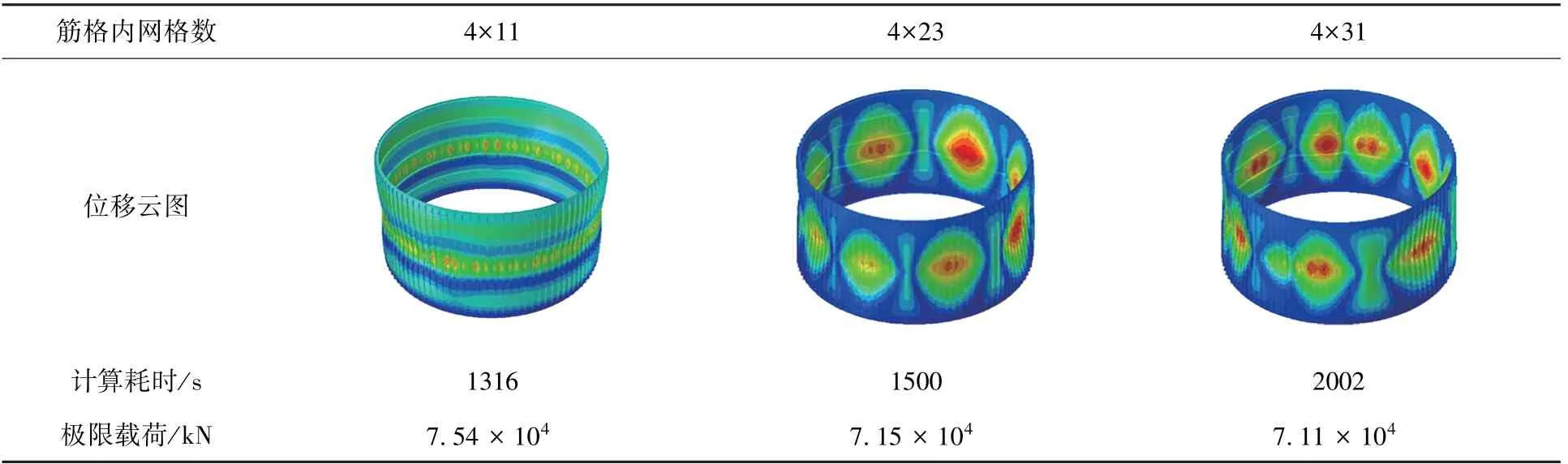
表2 不同蒙皮网格规模下结构整体失稳位移云图Table 2 Collapse displacement fringes in different skinned grid scale

图4 筋格内的网格数为4×23Fig.4 The number of grids in the rib is 4×23

代理模型利用已知样本点的输出值来预测未知点的输出值。 目前常用的代理模型有响应面模型、径向基函数代理模型、Kriging 代理模型和神经网络代理模型。 当问题的非线性程度较高时，多使用Kriging 代理模型[9]。 Kriging 模型是一种空间局部插值的方法，其基本思想是对已知函数进行加权来估计未知函数，并使得估计值与真实值之间的方差最小且数学期望相同的一种方法[15]。

设x0为未观测的需要估值的点，x1，x2，…，xN为周围的观测点，观测值相应为y(x1)，y(x2)，…，y(xN)。 未观测点的估计值记为~y(x0)，它由相邻观测点的已知观测值加权求和得到[16]，如式(2)所示：

其中，λi为待定的加权系数。

采用R2检验作为代理模型近似能力的评价标准，R2的表达式如式(3)所示：

其中，[xi，y(xi)] 为待验证样本点，s(xi) 为代理模型xi处的预测值， ¯y 为待验证样本点输出的平均值。 R2的取值范围在[0，1]之间，且值越大(越接近于1)，拟合的精度越高，当R2＞0.9 时，可认为代理模型具有足够高的拟合精度。

3.3 分步优化策略

在蒙皮桁条结构中，桁条是承受轴向力的主要结构，它提升了蒙皮的受压、受剪失稳临界应力；中间框通过支撑纵向桁条以提高桁条稳定性并增加结构径向刚度，从而提高蒙皮桁条结构的承载能力。 范书群等[7]对大直径火箭半硬壳结构框-桁匹配性研究表明，桁条在两框中间发生弯曲失稳时，中间框也同时失稳，此时结构为最优设计形式。 因此在第一步对桁条结构参数进行优化设计时，中间框设计得足够强，以确保桁条在两框之间发生失稳破坏。 在第二步优化时，基于桁条结构参数优化结果，对中间框结构参数进行优化，具体流程如图5 所示。 其总体思想是利用试验设计方法选取样本点，为缩短设计周期，利用高性能计算机群对样本点进行后屈曲分析得到其结构质量和极限载荷，根据样本点的输入-输出关系构建Kriging 代理模型。 对蒙皮桁条结构参数进行合理分组后，采用基于多岛遗传算法(Multi-Island Genetic Algorithm， MIGA)和修正可行方向算法(Modified Method of Feasible Directions， MMFD)的组合优化算法对蒙皮桁条结构进行分步优化。组合优化算法能充分发挥全局优化算法和梯度优化算法的优势，在全局空间内高效、准确地找到最优解。

本文研究主要耗时集中在对构建代理模型所需的初始样本点的有限元计算上，采用高性能计算机对单个样本点进行单次有限元计算耗时约20 分钟。 为缩短计算耗时，提高优化效率，本文基于高性能计算机群并行计算多个初始样本点，对初始样本点的后屈曲分析时间减少了约3/4，能极大地缩减设计周期。

图5 优化流程图Fig.5 Flow chart of optimization

4 蒙皮桁条结构轻质优化算例

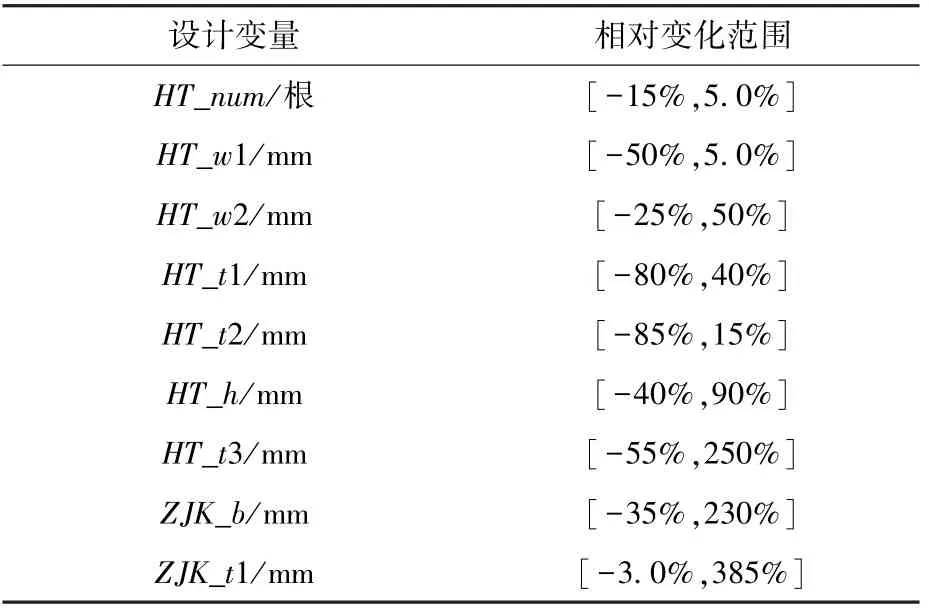
表3 蒙皮桁条结构参数变化范围Table 3 Parameter range of the skinned truss structure

4.1 桁条选型及参数优化

优化后的桁条结构参数相对初始值的变化量如图6 所示，横坐标中Mass 代表蒙皮桁条结构的质量。 可以看出，进行优化后，相较于初始设计结构，“Π”型截面桁条的结构质量减轻了6.3%，而“I”型截面桁条的结构质量减轻了2.9%，说明“Π”型截面结构的承载效率更高。 因此，选取“Π”型截面桁条进行后续的优化研究。

4.2 中间框参数优化

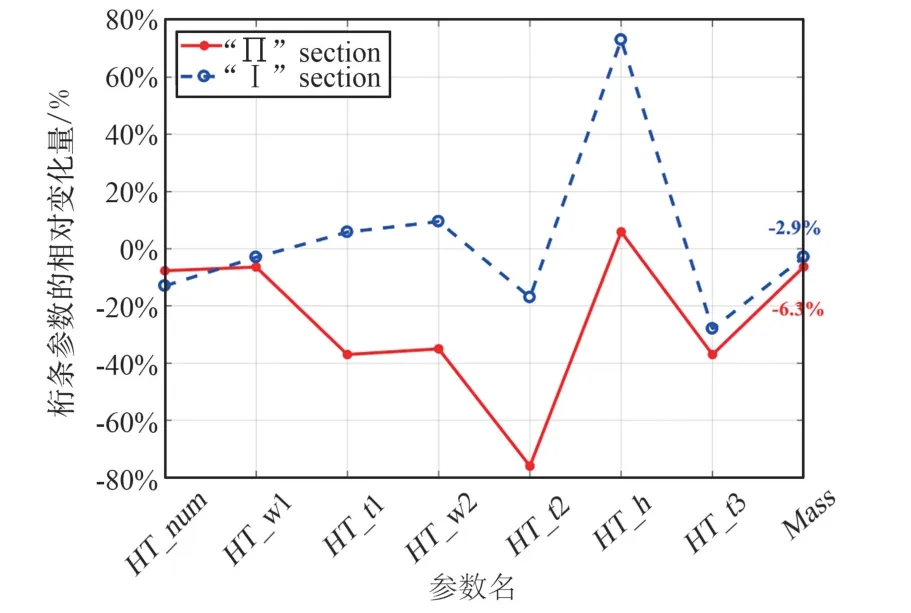
图6 优化后的桁条结构参数相对变化量Fig.6 Relative change of structural parameters of optimized trusses

对中间框结构参数进行优化后，优化后的蒙皮桁条结构参数、质量和极限载荷相对初始值的变化量如图7 所示。 可以看出，优化后的蒙皮桁条结构相较于初始设计结构，质量减轻16%，减重效果明显。 优化后蒙皮桁条结构位移-载荷曲线如图8 所示，结构极限载荷为7.01×104kN，大于结构的设计载荷， 说明优化后的蒙皮桁条结构的承载能力满足要求。

图7 优化后的蒙皮桁条结构参数相对变化量Fig.7 Relative changes of structural parameters of the skinned trusses

图8 蒙皮桁条结构位移-载荷曲线Fig.8 Displacement-loading curve of skinned trusse structure

5 结论

本文针对蒙皮桁条结构轻质优化设计中变量类型众多且有限元分析耗时长的问题，采用基于Kriging 代理模型和组合优化算法的分步优化策略开展优化研究。 主要结论如下：

1) 计算耗时随着蒙皮网格规模增加而增加。当蒙皮网格达到一定规模时，提升网格规模，极限载荷的计算结果相差较小。 综合考虑计算精度和效率，采用筋格内网格数量为4×23 的蒙皮网格；

2) 采用高性能计算机群对初始样本点进行并行计算，计算耗时减少了约3/4，极大地缩减了设计周期；采用组合优化方法能充分发挥全局优化算法和梯度优化算法的优势，便于在全局空间更快找到最优解，二者综合使优化效率得到提升；

3) 相较于“I”型截面桁条的蒙皮桁条结构，“Π”型截面结构承载效率更高；

4) 相较于初始设计，优化后的蒙皮桁条结构减重16%，且满足承载能力要求，验证了所提方法的有效性。

参考文献(References）

[ 1] 梅勇， 雷勇军， 冯韶伟， 等. 超静定捆绑火箭传力路径的组合优化策略[J]. 南京航空航天大学学报， 2016， 48(06)： 909-916.

Mei Y， Lei Y J， Feng S W， et al. Combination optimization strategy for load trans-path of hyper-static strap-on launch vehicle [J]. Journal of Nanjing University of Aeronautics ＆ Astronautic， 2016， 48(06)： 909-916.(in Chinese)

[ 2] Hao P， Wang B， Li G， et al. Hybrid optimization of hierarchical stiffened shells based on smeared stiffener method and finite element method[J]. Thin-Walled Structures， 2014，82： 46-54.

[ 3] Quinn D， Murphy A， Glazebrook C. Aerospace stiffened panels initial sizing with novel skin sub-stiffening features[J]. International Journal of Structural Stability and Dynamics，2013， 12(5)： 531-542.

[ 4] Wang B， Tian K， Hao P， et al. Load-carrying capacity and imperfection-sensitivity analysis of hierarchical stiffened panels[J]. Solid Rocket Technology， 2014， 37： 408-412.

[ 5] Wang B，Hao P，Li G，et al. Generatrix shape optimization of stiffened shells for low imperfection sensitivity[J]. Science China Technological Sciences， 2014， 57(10)： 2012-2019.

[ 6] 郝鹏. 面向新一代运载火箭的网格加筋柱壳结构优化研究[D]. 大连：大连理工大学，2013.

Hao P. Optimum Design of Stiffened Shell Structures for New Generation Launch Vehicle [D].Dalian： Dalian University of Technology， 2013. (in Chinese)

[ 7] 范书群，戴政，黄诚，等. 大直径火箭半硬壳结构框-桁匹配性设计[J]. 强度与环境， 2015， 42(3)： 34-41.

Fan S Q， Dai Z， Huang C， et al. Matching design of framestringer for large scale semigrid launch vehicle cylindrical structure[J]. Structure ＆ Environment Engineering， 2015，42(3)： 34-41. (in Chinese)

[ 8] 张铁亮， 丁运亮. 复合材料加筋壁板的结构布局优化设计[J]. 南京航空航天大学学报， 2010， 42(1)： 8-12.

Zhang T L， Ding Y L. Structural layout optimization of composite stiffened panel[J]. Journal of Nanjing University of Aerona Utics ＆ Astronautics， 2010， 42(1)： 8-12. (in Chinese)

[ 9] 张柱国，姚卫星，刘克龙. 基于进化Kriging 模型的金属加筋板结构布局优化方法[J]. 南京航空航天大学学报，2008(04)： 497-500.

Zhang Z G， Yao W X， Liu K L. Configuration optimization method for metallic stiffened panel structure based on updated kriging model[J]. Journal of Nanjing University of Aerona Utics ＆ Astronautics， 2008(04)： 497-500. (in Chinese)

[10] 郝鹏， 王博， 邹威任， 等. 基于RBF 模型的蒙皮桁条结构减轻孔优化[J]. 固体火箭技术， 2015， 38(05)： 717-721.

Hao P， Wang B， Zou W R， et al. Optimum design of lightening holes for skin-stringer structures based on RBF model[J]. Journal of Solid Rocket Technology， 2015， 38(05)：717-721.(in Chinese)

[11] 张希. 基于显式有限元方法的蒙皮桁条结构稳定性分析方法[C]/ /北京力学会第十九届学术年会论文集， 北京，2013： 495-496.

Zhang X. Stability analysis method of skin truss structure based on explicit finite element method [C]/ / Proceedings of the 19thAnnual Academic Meeting of the Beijing Institute of Mechanics， Beijing， 2013：495-496. (in Chinese)

[12] 郝鹏， 王博， 李刚， 等. 基于代理模型和等效刚度模型的加筋柱壳混合优化设计[J]. 计算力学学报， 2012， 29(4)： 541-548.

Hao P， Wang B， Li G，et al. Hybrid optimization of grid-stiffened cylinder based on surrogate model and smeared stiffener model[J]. Chinese Journal of Computational Mechanics，2012， 29(4)： 541-548. (in Chinese)

[13] 李洋， 赵斌， 龙连春. 网格疏密对加筋圆柱壳有限元计算的影响分析[C]/ /北京力学会第17 届学术年会论文集，北京，2011： 392-393.

Li Y， Zhao B， Long L C. Influence of reinforced cylindrical shell’s grid density on finite element calculation[C]/ /Proceedings of the 17thAnnual Conference of Beijing Mechanics Society， Beijing， 2011： 392-393. (in Chinese)

[14] Dominguez A， Stiharu I，Sedaghati R. Practical design optimization of truss structures using the genetic algorithms[J]. Research in Engineering Design， 2006(17)： 73-84.

[15] 安俊虎. 空间燃料站贮箱结构优化设计[D]. 大连：大连交通大学， 2018.

An J H. Optimum Structural Design for Tank of Space Fuel Station[D]. Dalian：Dalian Jiaotong University， 2018. (in Chinese)

[16] 韩忠华. Kriging 模型及代理优化算法研究进展[J]. 航空学报， 2016， 37(11)： 3197-3225.

Han Z H. Kriging surrogate model and its application to design optimization：A review of recent progress[J]. Acta Aeronautica ET Astronautica Sinica， 2016， 37(11)： 3197-3225. (in Chinese)