仿骨单位薄壁结构轴向和斜向耐撞性研究

范晓文，杨 欣，许述财，黄 晗，霍 鹏

(1. 河北农业大学机电工程学院，保定071000； 2. 清华大学汽车安全与节能国家重点实验室，北京100084)

1 引言

薄壁结构具有优良的耐撞性、理想的变形模式和令人满意的经济性，广泛应用于军事装备、航天器和汽车的防护[1-3]。 为提高薄壁结构的吸能性能，国内外研究人员通过理论分析、冲击试验和有限元模拟对其进行了大量的研究[4-7]。 Liang等[8]总结了多种适用于金属薄壁材料应变速率敏感特性研究的本构模型，如Cowper-Symonds 模型、Johnson-Cook 模型、Zerilli-Armstrong 模型、BP- partom 模型和Khan-Huang 模型等。 Baroutaji等[9]通过冲击和仿真试验对圆管、方管、锤形管、多胞管等常规管及波纹管、开孔管等非常规管进行了轴向、斜向、径向或横向的吸能特性和变形模式的研究。 虽然上述研究通过改变薄壁结构的几何形状改善了其耐撞性，但复杂的几何结构和多胞结构增加了薄壁结构自身质量，难以制造和应用。 因此，应以结构轻量化为前提，探寻简单且合理的结构，将其应用到薄壁管的优化设计中。

自然界中，许多生物已进化出以最轻质量承受最大外力的耐撞结构，随着工程仿生技术的发展，研究人员设计了各种仿生薄壁结构[10]。 Yin等[11]基于木贼类植物的茎结构设计了6 种具有不同截面结构的仿生管，通过有限元法研究了仿生管在轴向和横向载荷下的耐撞性。 研究表明，仿生管的耐撞性优于圆管和方管，且其壁厚、内管直径和晶胞数显著影响其耐撞性。 许述财等[12]基于竹结构设计了由仿生节、仿生单元和仿生内管组成的仿生管，利用有限元法模拟了仿生管的轴向碰撞吸能特性，并利用响应面法求得了仿生管的最优结构。 邹猛等[13]以牛角为生物原型提取了影响牛角耐撞性的结构特征参数，设计了仿牛角锥形薄壁管，比吸能(Specific Energy Absorption，SEA)比普通锥管高1.8 倍。 上述仿生结构虽有效提高了薄壁管的比吸能，但增加了薄壁结构的质量且提高了受冲击时的峰值载荷。 宋家锋等[14]受竹结构启发，设计了变厚度薄壁结构，通过仿真分析研究该结构在轴向冲击下的耐撞性，确定壁厚比和节长比为影响耐撞性的主要因素，但未对节数和壁厚对仿生管耐撞性的影响和仿生管在斜向冲击下的耐撞性进行研究。

除上述生物原型外，鹿角同样具有高强度和优异的耐撞性。 Kitchener[15]发现鹿角的比强度高于低碳钢，并确定鹿角结构可抵抗挠曲。 Chen等[16]对鹿角进行的压缩试验表明，干鹿角的纵向压缩强度约为197.3 MPa，远高于其横向压缩强度(66.7 MPa)。 通过对鹿角切片的显微观察发现，骨单位是鹿角的主要结构单元。 可见，骨单位的特殊结构对鹿角轴向和横向的力学性能有显著影响。 本文以骨单位为仿生原型，基于其微观结构，设计等梯度厚度薄壁结构，应用非线性有限元法对其进行仿真分析，采用全因子试验对其在轴向和斜向冲击载荷下的耐撞性进行研究，并采用加权优化法确定其最优结构。

2 仿骨单位薄壁结构设计

2.1 骨单位结构分析

骨单位(Osteon)，又称哈弗氏系统，为鹿角等长骨骨干主要结构单位[17]。 如图1 所示，骨单位呈内径相同而外径逐层加厚的圆管状，其长轴与鹿角的长轴平行，具有4～20 层同心环骨板结构，每层骨板的长度相等，自顶层至底层壁厚逐层递增，每层厚度增长值相等[18]。

图1 骨单位结构示意图Fig.1 Diagram of osteon structure

2.2 仿骨单位薄壁结构模型

提取骨单位的结构特征参数，分别定义为层数n、最大壁厚tmax和梯度值a，通过结构仿生，设计了1 种等梯度壁厚薄壁结构(Equal Gradient Thickness Thin-walled Structure，EGTTS)，其模型如图2 所示。 考虑实际应用，EGTTS 的长度l 和最大外径d 分别设定为120 mm 和50 mm。 由于骨单位每层骨板的长度相等且上下层骨板厚度的梯度值相等，EGTTS 每层的长度为120/n mm 且自上至下的梯度值a 为定值。

图2 EGGTS 结构示意图Fig.2 Diagram of EGGTS structure

使用Hypermesh 软件建立EGTTS 的有限元模型，管壁采用shell 单元。 为保证仿真精度和减少计算时长，将EGTTS 的有限元模型网格尺寸设定为2.5 × 2.5 mm[19]。 EGTTS 的材料为AA6061铝合金，材料参数如表1 所示。

表1 AA6061 铝合金材料参数Table 1 Material parameters of aluminum alloy AA6061

在EGTTS 模型的底端施加约束以固定模型，在其顶部设置质量为1000 kg 的移动刚性墙，如图3 所示，以10 m/s 的速度撞击EGTTS，撞击时间为10 ms。 仿真未考虑EGTTS 的材料失效。

图3 EGTTS 有限元模型撞击载荷示意图Fig.3 Diagram of impact load of finite element model of EGTTS

2.3 有限元模型的验证

加工制作的EGGTS 样件如图4 所示，尺寸如表2 所示，材料为铝合金AA6061，在室温环境下对EGGTS 样件进行压缩试验，以验证其有限元模型的有效性。 冲击试验中，落锤质量约为211 kg，落锤距样件顶端的掉落垂直高度为5.5 m(落锤自由落体至样件顶端时，落锤速度为10 m/s)。 通过计算，此时落锤动能远大于EGTTS 样件所能吸收的能量，可使样件充分压缩。

表2 EGGTS 样件的尺寸Table 2 The size of EGGTS sample

图4 EGGTS 样件Fig.4 Sample of EGGTS

EGGTS 的试验与仿真结果对比如图5 所示。 由图5 可知，EGGTS 的位移-比吸能和位移-力曲线的仿真结果与试验结果基本一致。 随着位移的增加，试验所得的比吸能值先高于仿真值，后低于仿真值，最大误差为8%。 当压溃位移为2 mm 时，由于实际样件的铝合金材料与仿真分析中材料的高速应变率存在差异，因此EGGTS 样件在验证试验中出现仿真分析中未出现的初始峰值力；当压溃位移为20 mm 和40 mm 时，试验所得到的EGGTS 的力值略高于仿真值，这是由于仿真分析中EGGTS 被设置为壳体，不会出现应力集中现象，而真实试验中，在EGGTS 的壁厚发生梯度变化的位置会在变形时发生应力集中现象，因此EGGTS 的压溃力试验值会高于仿真值。

EGGTS 的试验与仿真变形模式对比如图6所示，仿真试验可较准确地反映实物结构的变形模式。 EGGTS 具有由顶层至底层壁厚逐层增加的结构特性，因此当受载发生变形时，EGGTS可以保持整体结构的稳定性，由顶层开始逐层进行渐进折叠变形。 但由于样件材料参数无法与仿真分析参数完全一致，实际材料粘度较低，因此试验中压溃位移为40 mm 时，EGGTS 出现撕裂现象，但仿真分析与试验中EGGTS 仍存在变形一致性。

综上，EGGTS 的仿真结果与样件试验结果差异较小，证明了EGGTS 有限元模型的有效性。

图5 EGGTS 仿真和试验的位移-比吸能和位移-力曲线对比图Fig. 5 Comparison of x-SEA curve and x-F curve in simulation and experiment of EGGTS

图6 EGGTS 仿真和试验变形模式对比图Fig.6 Comparison of deformation modes in simulation and experiment of EGGTS

3 不同结构参数的仿真分析

3.1 试验方案

设计三因素三水平仿真试验，将n、tmax和a 作为试验因素，分别设置4 层、5 层、6 层；2.8 mm、2.9 mm、3.0 mm；0.2 mm、0.3 mm、0.4 mm 等间距三水平，以探讨因素n、tmax和a 对EGGTS 耐撞性的影响，并寻求EGGTS 的最优结构。

以最优结构的EEGTS 为仿真分析对象，并选取与EEGTS 的长度、外径及最大壁厚相同的普通圆管(Cylindrical tube， CT)作为对照管，进行0°、10°、20°和30°碰撞载荷下的仿真对照试验，以研究EGGTS 在轴向和斜向冲击载荷下的吸能特性及变形模式。

3.2 薄壁结构耐撞性评价指标

为正确评估EGTTS 的耐撞性，选择比吸能、平均压溃力(Mean crushing force， MCF)、峰值压溃力(Peak crushing force， PCF)和压溃力效率(Crushing force efficiency， CFE) 作 为 评 价 指标[20]。

1)SEA：单位质量薄壁结构所吸收的能量，见式(1)。 SEA 是衡量薄壁结构吸能能力的重要参数，其值越高，薄壁结构吸能能力越强。

其中m 为薄壁结构的总质量，EA为薄壁结构被压溃过程中吸收的能量，如式(2)所示：

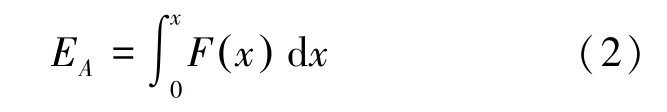
其中x 为压溃位移，F(x)为瞬时压溃力。

2)MCF：薄壁结构压溃过程中压溃力的平均值，如式(3)所示：

3)PCF：薄壁结构压溃过程中压溃力的最大值。 PCF 过大会造成碰撞过程中人员头部损伤指标(Head Injury Criterion， HIC)值过高，引起伤亡[21]。

4)CFE：MCF 与PCF 的比值，见式(4)。 CFE值越大，薄壁结构吸能效率越高。

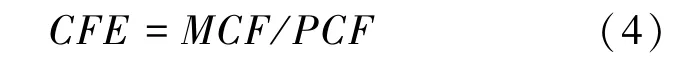
3.3 三因素三水平试验结果分析

利用LS-DYNA 软件对27 个(3×3×3)具有不同层数n、最大壁厚tmax和梯度值a 的EGGTS 进行仿真计算。 选择压溃过程的前100 mm 压溃位移计算耐撞性评价指标SEA、MCF、PCF 和CFE。

3.3.1 层数n 的影响

将27 种EGGTS 分为9 组，每组的3 个EGGTS 的n 不同(n ＝4、5、6 层)，而tmax与a 相同，如表3 所示。

表3 组A1 至A9 的设计变量值Table 3 Design variables from group A1 to A9

9 组具有不同n 的EGGTS 的SEA、MCF、PCF和CFE，如图7 所示。 由图7 可见，n 对EGGTS的SEA 影响较小，而对MCF、PCF 及CFE 的影响显著。 n ＝5 层时EGGTS 的SEA 较高，

而n ＝4 层时EGGTS 的SEA 较低。 当tmax和a 一定时，EGGTS 的n 越大，其顶端壁厚越小且壁厚变化次数越多，其MCF 与PCF 越低。但n ＝4 层的EGGTS 的CFE 较高，表明虽然该层数结构MCF 和PCF 较高，但其吸能效率也较高。

9 组EGGTS 中，n ＝6 层、tmax＝2.9 mm 且a ＝0.4 mm 的EGGTS 的SEA 最高，n ＝6 层、tmax＝2.8 mm 且a ＝0.3 mm 的PCF 最低。

3.3.2 最大壁厚tmax的影响

将27 种EGGTS 分为9 组，如表4 所示。 每组的3 个EGGTS 的tmax(tmax＝2.8 mm、2.9 mm、3.0 mm)不同，而n 与a 相同。 因CT 的n ＝1，a ＝0，仅tmax可变，所以仅在此节中进行27 种EGGTS与CT 耐撞性能的对比。

表4 组B1 至B9 的设计变量Table 4 Design variables from group B1 to B9

具有不同tmax的9 组EGGTS 和CT 的SEA、MCF、PCF 和CFE 如图8 所示。 由图8 可见，因具有等梯度壁厚结构，27 种EGGTS 的MCF和PCF 远低于CT，而多数EGGTS 的SEA 和CFE 高于CT，因此，等梯度壁厚结构的耐撞性能明显优于普通圆管。 tmax＝2. 9 mm 的EGGTS的SEA 较高，而tmax＝2. 8 mm 的EGGTS 的SEA较低。

EGGTS 的MCF 与PCF 随tmax的增大而提高，tmax＝2.8 mm 的EGGTS 的MCF 与PCF 总是最低，表明tmax＝2.8 mm 的结构可有效降低碰撞压溃力。 tmax＝3.0 mm 的EGGTS 的CFE 较高，表明其吸能效率较高。

图7 改变n 的9 组EGGTS 的耐撞性指标值Fig.7 Value of crashworthiness index of 9 groups of EGGTS with variable n

图8 改变tmax的9 组EGGTS 的耐撞性指标Fig.8 Value of crashworthiness index of 9 groups of EGGTS with variable tmax

3.3.3 梯度值a 的影响

将27 种EGGTS 分为9 组以研究a 对EGGTS的耐撞性的影响，每组的3 个EGGTS 的a 不同(a＝0.2 mm、0.3 mm、0.4 mm)，而n 与tmax相同，如表5 所示。

表5 组C1 至C9 的设计变量Table 5 Design variables from group C1 to C9

9 组具有不同a 的EGGTS 的SEA、MCF、PCF和CFE 如图9 所示。 a ＝0.4 mm 的EGGTS 的MCF 和PCF 较低，这是由于当n 与tmax相同时，a越大，EGGTS 自上至下每层壁厚越小，因此其MCF 和PCF 越低。 而a ＝0.3 mm 的EGGTS 具有最高的SEA 与CFE，表明其具有较好的吸能能力与压溃稳定性。 9 组EGGTS 中，tmax＝2.9 mm、n ＝6 层且a ＝0.4 mm 的EGGTS 的SEA 最高，tmax＝2.8 mm、n ＝6 层且a ＝0.3 mm 的EGGTS 的PCF最低。

综上，层数n、最大壁厚tmax和梯度值a 对EGGTS 的耐撞性有显著影响，但3 个参数对EGGTS 各耐撞性指标的影响程度不同，导致各类EGGTS 的耐撞性存在差异，所以确定最优的结构参数组合对提高EGGTS 的耐撞性具有重要意义。

3.3.4 确定最优结构参数组合

采用加权计算的方法来评价27 种具有不同结构参数的EGGTS 的耐撞性优劣，选择SEA、PCF 和CFE 为评价指标，以式(5)计算27 种EGGTS 的权值。

式中，α1、α2、α3是3 个评价指标的权重因子，且α1＋α2＋α3＝1，取α1＝0.4，α2＝α3＝0.3[22]。 通过SEA/SEAmax、PCF/PCFmax和CFE/CFEmax运算进行无量纲化处理。

图10 显示出了27 种EGGTS 的W 值，由图可知n ＝6 层、tmax＝2.8 mm、a ＝0.3 mm 的EGGTS 具有最大的W，这表明具有此结构参数组合的EGGTS 耐撞性最优。

图9 改变a 的9 组EGGTS 的耐撞性指标Fig.9 Value of crashworthiness index of 9 groups of EGGTS with variable a

图10 27 种EGGTS 的W 值Fig.10 W value of 27 kinds of EGGTS

3.4 EGGTS 和CT 对照试验

3.4.1 吸能特性分析

选择具有最佳结构参数组合的EGGTS(n ＝6层、tmax＝2.8 mm、a ＝0.3 mm)和具有相同l、d 和tmax的CT 进行0°、10°、20°和30°冲击载荷下的对照仿真试验。 图11 ～图14 分别为EGGTS 和CT在0°、10°、20°和30°冲击载荷下的位移-比吸能与位移-载荷曲线图。

由图11 可得，轴向(0°)冲击载荷下，EGGTS和CT 的SEA、MCF、PCF、CFE 分别为41.43 kJ/kg、31.86 kN、 54.02 kN、 58.98% 和 40.13 kJ/kg、55.35 kN、107.47 kN、51.50%。 EGGTS 的SEA、CFE 较CT 提高了3.2%、14.5%，而MCF、PCF 降低了30.9%、42.4%。 前90 mm 压溃位移的CT 表现出更佳的吸能能力，而EGGTS 在压溃位移为70 mm时，由于其壁厚增大，参与变形的结构增多，吸能能力大幅提高，随压溃位移增加，EGGTS 的SEA 高于CT。 观察位移-载荷曲线，CT 在压溃过程中出现初始峰值压溃力，随后压溃力按照一定频率波动，而由于EGGTS 顶层壁厚较薄，不存在初始峰值压溃力，且压溃力随压溃过程中壁厚的逐层增加而逐渐增大。

由图12 可得，10°冲击载荷下，EGGTS 和CT的SEA、MCF、PCF、CFE 分别为27.47 kJ/kg、29.09 kN、56.93 kN、51.10% 和31.84 kJ/kg、56.43 kN、85.87 kN、65.72%。 EGGTS 的SEA、CFE 较CT 降低了13.7%、22.2%，但MCF、PCF降低了48.4%、33.3%。 10°冲击载荷下，EGGTS未出现吸能量大幅增加的现象，但呈现出加速提高的趋势，其SEA 低于CT。 而由于EGGTS 自上至下壁厚逐层递增的结构特性，未出现初始峰值压溃力，载荷曲线随壁厚的增加而波动上升，其MCF、PCF 远低于CT。

图11 0°载荷下位移-吸能比和位移-载荷曲线图Fig.11 x-SEA and x-F curves under 0° load

由图13 可得，20°冲击载荷下，EGGTS 和CT的SEA、MCF、PCF、CFE 分别为21.64 kJ/kg、25.14 kN、49.86 kN、50.42% 和18.13 kJ/kg、37.14 kN、79.53 kN、46.70%。 EGGTS 的SEA、CFE 较CT 提高了19.3%、8.0%，而MCF、PCF 降低了32.3%、37.3%。

由图14 可得，30°冲击载荷下，EGGTS 和CT的SEA、MCF、PCF、CFE 分别为15.14 kJ/kg、18.22 kN、34.49 kN、52.82% 和13.69 kJ/kg、29.98 kN、61.57 kN、48.70%。 EGGTS 的SEA、CFE 较CT 提高了10.6%、8.5%，而MCF、PCF 降低了39.2%、44.0%。 EGGTS 和CT 在20°与30°冲击载荷下的位移-比吸能曲线和位移-载荷曲线呈现出相近的变化趋势。 EGGTS 的SEA 开始低于CT，但随压溃位移的增加而大幅提高，最终超过CT。 观察位移-载荷曲线，EGGTS 的载荷呈现递增波动的趋势，这与其自上至下壁厚逐层递增的结构特点相呼应。 而CT 仍出现远高于EGGTS峰值压溃力的初始峰值压溃力，其降低初始碰撞加速度的能力低于EGGTS。

图12 10°载荷下x-SEA 和x-F 曲线图Fig.12 x-SEA and x-F curves under 10° load

3.4.2 变形模式分析

图15～图18 分别为EGGTS 和CT 在0°、10°、20°、30°冲击载荷下的变形模式图。 0°和10°冲击载荷下，EGGTS 始终呈现稳定的渐进折叠变形模式，未发生失稳和坍塌现象。 0°冲击载荷下，CT首先发生渐进折叠变形，当褶皱数量增加后，其下部失稳导致大幅度折叠变形。 而在10°冲击载荷下，CT 经历较长时间的渐进折叠变形后失稳，并发生坍塌。

20°和30°冲击载荷下，由于GEETS 具有自上至下壁厚逐层递增的结构，仍保持稳定的渐进折叠变形模式，褶皱数量随冲击角度的增大而减少，未出现塌陷和整体弯曲现象，具有较强的吸能能力。 而CT 由于壁厚相等，仅有少部分结构发生折叠变形，随后发生整体弯曲变形，且冲击角度越大，发生整体弯曲的时间越早。 整体弯曲变形模式使CT 的大部分结构未发生变形，导致其能量吸收大幅减少，吸能能力大幅降低。 可见，仿生薄壁结构在承受高角度的冲击载荷时，具有理想的变形模式和更广泛的应用空间。

图13 20°载荷下x-SEA 和x-F 曲线图Fig.13 x-SEA and x-F curves under 20° load

图14 30°载荷下x-SEA 和x-F 曲线图Fig.14 x-SEA and x-F curves under 30° load

图15 0°冲击载荷下EGGTS 和CT 的变形模式图Fig.15 Diagram of deformation modes of EGGTS and CT under 0° impact load

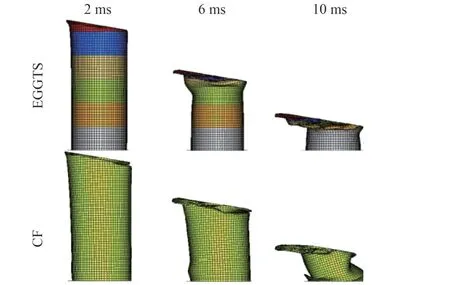
图16 10°冲击载荷下EGGTS 和CT 的变形模式图Fig.16 Diagram of deformation modes of EGGTS and CT under 10° impact load

图17 20°冲击载荷下EGGTS 和CT 的变形模式图Fig.17 Diagram of deformation modes of EGGTS and CT under 20° impact load

图18 30°冲击载荷下EGGTS 和CT 的变形模式图Fig.18 Diagram of deformation modes of EGGTS and CT under 30° impact load

4 结论

1)轴向冲击载荷下，层数为6、最大壁厚为2.8 mm、梯度值为0.3 mm 的仿生薄壁结构具有最优的耐撞性。

2)较同外径及最大壁厚的普通圆管，仿生薄壁结构的质量降低了31.3%，比吸能分别提高了3.2%、-13.7%、19.3%和10.6%，而峰值压溃力分别降低了42.4%、33.3%、37.3%、44.0%。 在0°、10°、20°、30°载荷下，仿生薄壁结构始终呈现稳定的渐进折叠变形模式，而随载荷角度的增加，普通圆管由渐进折叠变形模式转变为整体弯曲变形模式。 因此，仿生薄壁结构的吸能特性和变形模式较普通圆管在实际应用中更具优势。

3)将骨单位的结构特征应用到薄壁结构的设计中，可以提高薄壁结构的耐撞性能，降低质量，可作为航天器吸能元件轻量化设计的参考。

参考文献(References）

[ 1] Miller W S， Zhuang L， Bottema J， et al. Recent development in aluminum alloys for the automotive industry[J]. Materials Science and Engineering： A， 2000， 280(1)： 37-49.

[ 2] Toros S，Ozturk F，Kacar I. Review of warm forming of aluminum-magnesium alloys[J]. Journal of Materials Processing Technology， 2008， 207(1-3)： 1-12.

[ 3] Bartczak B，Gierczycka-zbrozek D，Gronostajski Z， et al. The use of thin-walled sections for energy absorbing components：a review[J]. Archives of Civil and Mechanical Engineering，2010， 10(4)： 5-19.

[ 4] Cao J， Amir K， Gan N F， et al. Crashworthiness of functionally graded density aluminum foam-filled tapered thin-walled structures[J]. Journal of Automotive Safety and Energy，2016， 7(01)： 35-48.

[ 5] 邹猛， 魏灿刚， 许述财， 等. 汽车碰撞中锥形晶胞薄壁金属管吸能特性的仿真研究[J]. 汽车安全与节能学报，2012， 3(04)： 326-331.

Zou M， Wei C G， Xu S C， et al. Simulation study on energy absorption characteristics of tapered cell thin-walled metal tube in automobile collision[J]. Journal of Automotive Safety and Energy， 2012， 3(04)： 326-331. (in Chinese)

[ 6] Abramowicz W. Thin-walled structures as impact energy absorbers[J]. Thin-Walled Structures， 2003， 41(2-3)： 91-107.

[ 7] Qiu X M， Yu T X. Some topics in recent advances and applications of structural impact dynamics[J]. Applied Mechanics Reviews， 2011， 64(3)： 034001-1-034001-12

[ 8] Liang R， Khan A S. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures[J]. International Journal of Plasticity， 1999， 15(9)： 963-980.

[ 9] Baroutaji A， Sajjia M， Olabi A G. On the crashworthiness performance of thin-walled energy absorbers： recent advances and future developments[J]. Thin-Walled Structures， 2017，118： 137-163.

[10] 任露泉， 梁云虹. 仿生学导论[M]. 北京： 科学出版社，2016： 32-65.

Ren L Q， Liang Y H. Introduction to Bionics[M]. Beijing：Science Press， 2016： 32-65.(in Chinese)

[11] Yin H， Xiao Y， Wen G， et al. Crushing analysis and multiobjective optimization design for bionic thin-walled structure[J]. Materials ＆ Design， 2015， 87： 825-834.

[12] 许述财， 邹猛， 魏灿刚， 等. 仿竹结构薄壁管的轴向耐撞性分析及优化[J]. 清华大学学报(自然科学版)， 2014，54(03)： 299-304.

Xu S C，Zou M，Wei C G，et al. Axial crashworthiness analysis and optimization of a bionic thin-walled tube based on bamboo structure. [J]. Journal of Tsinghua University(Science and Technology)， 2014， 54(03)： 299-304. (in Chinese)

[13] 邹猛， 于用军， 张荣荣， 等. 仿牛角结构薄壁管吸能特性仿真分析[J]. 吉林大学学报(工学版)， 2015， 45(6)：1863-1868.

Zou M，Yu Y J，Zhang R R，et al.Simulation analysis of energyabsorption properties of thin-wall tube based on horn structure[J]. Journal of Jilin University(Engineering and Technology Edition)，2015，45(6)：1863-1868. (in Chinese)

[14] 宋家锋， 王会霞， 盖宏健， 等. 基于竹结构的薄壁吸能管仿生优化研究[J]. 载人航天， 2017， 23(04)： 473-481.

Song J F， Wang H X， Gai H J， et al. Bionic optimization design of thin-walled energy absorption tube inspired by bamboo structure[J]. Manned Spaceflight， 2017， 23(04)： 473-481.(in Chinese)

[15] Kitchener A C. Biomechanics and Evolution[M]. Cambridge University Press， 1991：43-50.

[16] Chen P Y， Stokes A G， McKittrick J. Comparison of the structure and mechanical properties of bovine femur bone and antler of the North American elk(Cervus elaphus canadensis)[J]. Acta Biomaterialia， 2009， 5(2)： 693-706.

[17] Robling A G， Stout S D. Morphology of the drifting osteon[J]. Cells Tissues Organs， 1999， 164(4)： 192-204.

[18] Cooper D M L，Erickson B，Peele A G，et al. Visualization of 3D osteon morphology by synchrotron radiation micro-CT[J].Journal of Anatomy， 2011， 219(4)： 481-489.

[19] 林云成， 宋家锋， 刘升福， 等. 基于竹节结构的保险杠横梁仿生优化及仿真分析[J]. 汽车安全与节能学报， 2018，9(04)： 410-417.

Lin Y C，Song J F，Liu S F， et al. Bionic design optimization and simulation analysis of bumper beam inspired by the structure of bamboo node[J]. Journal of Automotive Safety and Energy， 2018， 9(04)： 410-417. (in Chinese)

[20] Chen B C，Zou M，Liu G M，et al. Experimental study on energy absorption of bionic tubes inspired by bamboo structures under axial crushing[J]. International Journal of Impact Engineering， 2018， 115： 48-57.

[21] 马伟杰， 史永万， 刘志新. 基于线性回归的头部损伤评价指标分析[J]. 中国汽车， 2019(08)： 52-56.

Ma W J， Shi Y W， Liu Z X. Analysis of head injury criteria based on linear regression[J]. China Auto， 2019(08)： 52-56.(in Chinese)

[22] Song J F，Xu S C，Wang H X，et al. Bionic design and multiobjective optimization for variable wall thickness tube inspired bamboo structures [J]. Thin-Walled Structures， 2018， 125：76-88.