足垫垂直冲击月壤理论模型研究

武士轻，王永滨*，候绪研，薛萍萍，龙 龙

(1. 北京空间机电研究所，北京100094； 2. 哈尔滨工业大学机电工程学院，哈尔滨150001)

1 引言

着陆器月面着陆冲击特性是决定着陆任务成败的关键因素，过大的着陆冲击将直接导致内部仪器失效，进而影响后续的月面实地探测任务，特别是载人登月任务对着陆冲击响应提出了更高的要求。 因此，量化分析着陆冲击过程对提升着陆器的着陆可靠性、保障航天任务的实施具有十分重要的意义。

着陆器着陆过程中，足垫与月壤首先接触，相互作用，伴随着月壤颗粒飞溅、错动、滑移，与着陆器缓冲机构一起吸收着陆冲击的能量。 此过程中，足垫承受的冲击力将直接传递至着陆器上，足垫侵入月壤的深度将影响着陆器的倾斜姿态。 因此足垫冲击月壤颗粒的动力学行为对着陆器的着陆安全性及稳定性有直接的影响。

在仿真方面，目前利用的手段集中在多体动力学、有限元、离散元仿真工具上。 曾福明[1]运用MSC 软件对着陆器缓冲性能进行仿真分析，结合实验验证，其柔性多体动力学方法建立的着陆器冲击模型与实测数据基本吻合，该结论指导了工程实现。 蒋万松等[2]基于MSC 软件的二次开发模块，建立了考虑铝蜂窝材料缓冲作用和月壤力学性质的动力仿真模型，研究了着陆器在不同地面坡度和月壤物理性质条件下的着陆性能，并进行了着陆冲击离散元仿真研究，探讨了着陆过程的能量耗散路径。 陈金宝等[3]针对未来目标天体表面低重力场模拟，推导了探测器软着陆动力学相似性关系，利用瞬态动力学仿真软件进行了验证。 万峻麟等[4]针对典型月壤，利用DYTRAN 软件开展了动力学研究，表明多级铝蜂窝缓冲器具有较好的缓冲性能，同时指出月壤物理机械性能有待深入研究。 梁东平[5]利用ABAQUS软件建立了月壤模型，对均布静荷载作用下月壤的变形进行了分析。 邹猛等[6]基于颗粒流程序PFC3D 对月壤静力学特性进行了离散元模拟研究，描述了月面探测车辆行驶下的月壤承压特性模型与剪切特性模型。

在理论及试验研究方面，可以借鉴土力学对刚体冲击土体的研究，例如基于强夯法固结理论的动力固结模型、Scott 的阻尼自由振动模型。 钱家欢等[7]考虑了加卸载过程对Scott 模型进行了改进。 郭见扬[8]将刚体与地基的接触力变化简化为三角形而开展了方法研究。 高有斌等[9]对加卸载过程加入应力修正系数。 牛志荣等[10]在研究土体受冲击时，依据土体的塑性极限相对于冲击动量和土体的刚度系数之间的比例关系，将冲击过程进行了细分。 钟世英[11]结合有限元及大量试验对NASA 模型进行了改进，其模型计算结果与试验测试结果具有一致的变化趋势，冲击时间的计算值与测试值相差不大。

以上研究偏重于借助仿真及试验进行运动缓冲特性分析，仿真计算周期及成本较高，缓冲试验离散度较大，可重复性差。 为能够从理论层面更好地分析足垫运动特性、更快地预测实验测试结果，指导工程应用，同时弥补仿真计算周期长的缺点，本文将细化冲击过程，构建足垫垂直冲击月壤的理论模型，提取足垫冲击过程的动力学特征参数，并将仿真结果与理论计算进行对比。

2 理论模型构建

以着陆器足垫为研究对象，冲击过程分为加载阶段和卸载阶段，见图1。 根据月壤对足垫的作用列力平衡微分方程，进行求解。

图1 典型着陆过程Fig.1 Typical landing process

将足垫简化为球形，如图2 所示，在冲击过程中，足垫与月壤的接触半径r 不断增大，R 为足垫球面轮廓半径，Z 为侵入月壤深度，M 为足垫质量，F 为足垫所受轴向力。

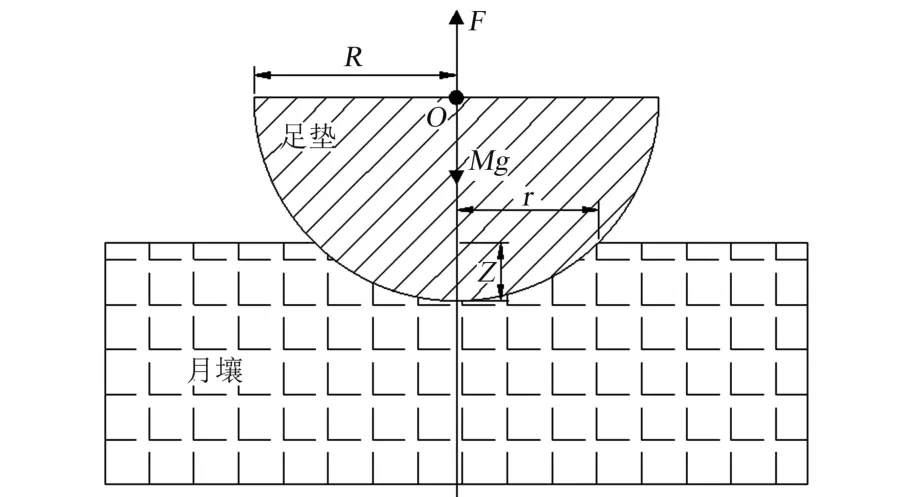
图2 足垫受力示意图Fig.2 Force on the foot pad

足垫冲击月壤，月壤的密实度随之发生变化，月壤对足垫的冲击作用也随之发生变化，采用Bekker 模型[12]来模拟此过程，该模型是把月壤颗粒当作变刚度的弹簧。 卸载阶段足垫正下方的月壤密实度相对稳定，参考岩土力学的强夯固结理论可以建立卸载阶段的微分方程。

2.1 加载阶段模型

在加载阶段，忽略月壤塑性及粘滞力(阻尼)对动力响应的作用，假设正方向为竖直向下，则足垫的力学方程为式(1)。

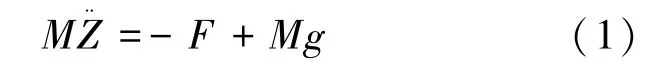
结合Bekker 提出的承压模型，足垫所受月壤平均正应力如式(2)所示。

式中，σ 为足垫单位面积法向应力，r 为足垫冲击接触半径，kc为月壤黏聚模量，一般取2.8 kN/mn＋1[13]，kφ为月面的摩擦模量，一般取820 kN/mn＋2[13]，n 为变形指数。

由式(1)、(2)得足垫的平衡方程如式(3)所示。

式中，x 为足垫运动位移。 根据初始下陷量和初始冲击速度得到2 个初始条件如式(4)、(5)所示。

将足垫简化为球形，如图2 所示，在冲击过程中足垫与月壤的接触半径r 与R 之间的关系如式(6)所示。

2.2 卸载阶段模型

在卸载阶段，即冲击过程的第二阶段，不考虑重力，此时接触区域月壤密实度已经接近稳定，足垫的基本动力学方程为式(7)。

式中，C 为月壤阻尼常数，S 为卸载阶段月壤弹性常数，如式(8)～(11)所示。

式中， r2为卸载阶段足垫与月壤接触面半径，其与R、x 关系亦满足式(6)，ρ 为月壤密度，E为月壤弹性模量，μ 为泊松比，S′为卸载阶段月壤等效刚度。 依据连续性条件，加载阶段结束时刻的位移、速度和加速度与卸载阶段初始时刻相等。

3 离散元模型

为了验证理论模型的正确性，结合EDEM 离散元软件进行仿真计算，采用滚动等效法，即采用球形模型通过放大球形颗粒间的滚动摩擦系数来模拟非球形月壤颗粒的特性。 利用Hertz-Mindlin无滑动接触模型，建立月壤的离散元模型，见图3。 参数查阅文献及采用模拟月壤进行实际测试，具体数据见表1[14-16]、表2[17]。 足垫材料为铝合金。 通过初步仿真分析，一定范围内颗粒的大小对仿真结果影响不大，因此结合计算效率，研究中将模拟月壤基本颗粒尺度定为直径1 mm。

图3 足垫冲击月壤离散元模型Fig.3 Discrete element model of foot pad impacting lunar soil

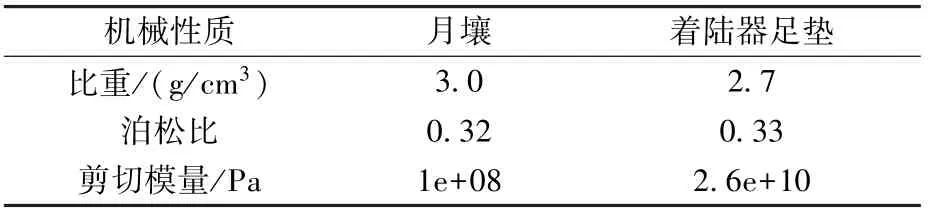
表1 仿真所用材料参数[14-16]Table 1 Material parameters used in the simulation[14-16]

表2 模型间相互作用参数[17]Table 2 Interaction parameters between models[17]

结合上述参数，进行了离散元分析。 不同时刻月壤颗粒速度云图如图4 所示。 通过提取月壤及足垫的运动速度，可以看出足垫冲击月壤过程集中在两者接触的前0.01 s。 在此过程中，足垫首先接触正下方的月壤，使其颗粒速度增加，受挤压的月壤颗粒以半椭圆球的影响区域向外扩展，足垫所受合力近似竖直，说明月壤的总体趋势是被向下压，仅在月壤表层出现少量颗粒飞溅，此过程与理论分析一致。

图4 足垫冲击月壤典型响应云图Fig.4 Typical response cloud map of foot pad impacting lunar soil

4 计算结果分析

影响足垫与月壤相互作用的参数主要是着陆速度、足垫质量和足垫着陆倾斜角度。 本文仅研究足垫垂直冲击月壤，因此以下针对不同的着陆速度及不同的足垫质量，分别利用理论模型及离散元仿真进行计算，提取足垫位移、轴向力等动力学信息，进行对比。

4.1 着陆速度

足垫冲击月壤速度分别为1 m/s、2 m/s、4 m/s、6 m/s，足垫质量设定为4 kg，足垫垂直冲击，月面坡度0°。

为了更直观地将仿真与理论模型进行对比，提取离散元仿真中的冲击速度所形成的月壤形貌，如图5。

理论模型不能体现撞击坑直径变化，但是可以计算得到撞击坑深度(侵入深度)。 足垫冲击月壤的侵入位移曲线如图6 所示，不同着陆速度下，足垫的动态响应曲线形态特征相似，峰值不同，说明不同着陆冲击速度下，足垫与月壤相互作用的过程相似。

图5 不同足垫冲击速度形成的月壤撞击坑形状Fig.5 The crater shape of lunar soil formed by different impact velocities of foot pads

图6 不同冲击速度下足垫的位移曲线Fig.6 Displacement curve of the foot pad under different impact speeds

足垫的位移及最终侵入深度与足垫初始冲击速度正相关，初始冲击速度越大，撞击坑深度越大，两者存在正相关关系。 卸载阶段足垫冲击的深度一定程度上反映月壤的密实度，稳定后的侵入深度一定程度上反映了月壤的变形程度，而且初始冲击速度越大，加载阶段结束得越快，冲击持续的时间越短。

如图7 所示，在加载阶段，随着足垫与月壤接触，月壤受挤压变形，月壤密实度越来越大，足垫所受轴向力迅速增大，轴向力的峰值与足垫初始冲击速度正相关。 冲击速度越大，轴向力刚开始的增长率越大，相应足垫速度减小且减小得越来越快。

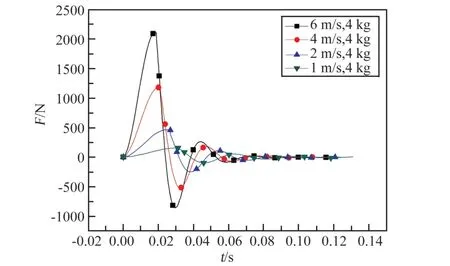
图7 不同着陆速度下，足垫轴向力随时间的变化Fig.7 Changes of axial force of foot pad with time at different landing speeds

当速度降低为0 时，开始卸载阶段，在卸载阶段，月壤密实度不再变化，但月壤的变形较大，随着月壤受挤压的变形恢复，对足垫有一定的反弹，此后着陆器会产生小幅度的振动，振幅越来越小，趋于平衡。

为了将理论模型计算结果与离散元仿真进行比对，特将离散元仿真中撞击坑外轮廓颗粒坐标提取并导入MATLAB 中，从而得到撞击坑深度H(侵入深度)与冲击速度v 的曲线。 两者侵入深度对比见图8，两者趋势一致，误差控制在13%以内。 离散元计算数值大于理论计算值，对曲线进行拟合，可以得出，其侵入深度与冲击速度成线性关系，其基本公式见图8。

图8 侵入深度对比(仿真与理论）Fig.8 Comparison chart of intrusion depth (simulation and theory）

轴向力对比见图9，理论分析与仿真趋势一致，误差在10%以内。 基于多项式拟合的基本公式见图9。 数值上，理论计算结果大于离散元仿真计算，分析其原因，理论模型中冲击加载阶段没有考虑月壤的塑性及阻尼效应。 因此，理论模型建立的月壤刚度较大，从而体现出侵入深度小，但是峰值轴向力大。

图9 峰值轴向力对比(仿真与理论）Fig.9 Comparison chart of peak axial force (simulation and theory）

4.2 足垫质量

足垫质量分别为2 kg、4 kg、6 kg、8 kg，着陆速度设定为4 m/s，足垫垂直冲击，月面坡度0°。

提取离散元仿真中的不同足垫质量冲击所形成的月壤形貌，如图10 所示。

图10 不同冲击质量下形成的月壤撞击坑形状Fig.10 Lunar impact craters formed under different impact masses

不同足垫冲击质量下，足垫的动态响应曲线形态特征一致，但是峰值不同。 如图11 所示，足垫的位移及侵入深度，与冲击质量正相关。 在0～0.01 s 加载阶段，虽然冲击质量不同，但是冲击位移近似相同。 后续，随着足垫与月壤的冲击碰撞，质量越大，其侵入的月壤深度越深。 经过卸载阶段后，撞击坑深度和冲击速度依旧正相关。 分析其原因，足垫冲击质量越大，其着陆携带动能越大，撞击坑的深度也越深，震荡衰减后的位移也越大，相应的冲击时间也越长。

如图12、图13 所示，轴向力的峰值与足垫冲击质量正相关。 在加载阶段，不同冲击质量下，轴向力刚开始几乎相同，因为不同足垫质量工况的冲击初速度是相同的，因此，不同质量的足垫的位移、速度近似，月壤的变形挤压近似，所以轴向力刚开始是近似的。 但是随着冲击过程的进行，同样的轴向力下，质量越小，正向加速度越大，速度越小，位移变化小，足垫受到恢复力小。

图11 不同冲击质量下足垫的位移曲线Fig.11 Displacement curve of foot pad under different impact masses

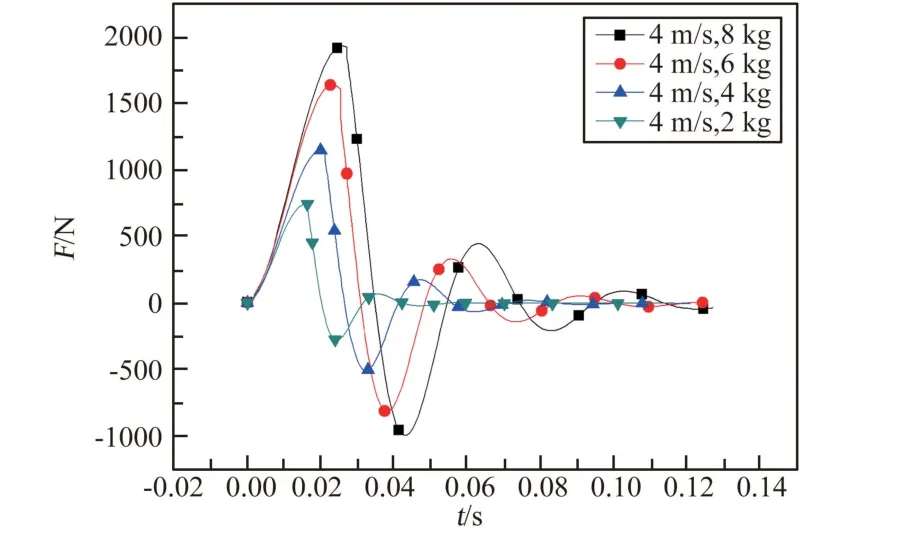
图12 不同冲击质量下，足垫轴向力随时间的变化Fig.12 Changes of axial force of foot pad with time for different impact masses

图13 不同冲击质量下，足垫加速度随时间的变化Fig.13 Changes of impact acceleration of foot pad with time for different landing masses

为了将理论模型计算结果与离散元仿真进行比对，特将撞击坑外轮廓颗粒坐标提取并导入MATLAB 中，得到撞击坑深度H(侵入深度)与足垫质量M 的曲线。 两者侵入深度对比见图14，两者趋势一致，误差在13%以内。 对曲线进行拟合，可以得出，侵入深度与足垫质量成线性关系，其公式见图14。

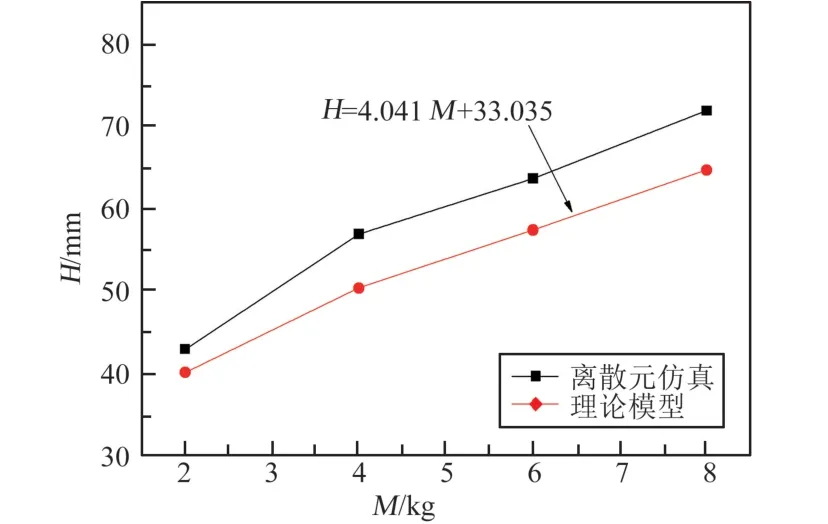
图14 侵入深度对比图(仿真与理论）Fig.14 Comparison chart of intrusion depth(simulation and theory）

轴向力对比见图15，理论分析与仿真趋势一致，误差在15%以内。 在此范围内，轴向力与足垫质量近似成线性，其基本公式见图15。 数值上，理论计算结果大于离散元仿真计算，因为理论模型冲击加载阶段没有考虑月壤的塑性及阻尼效应，因此，体现出来理论模型建立的月壤刚度较大，从而体现出来的侵入深度小，但是峰值轴向力大。

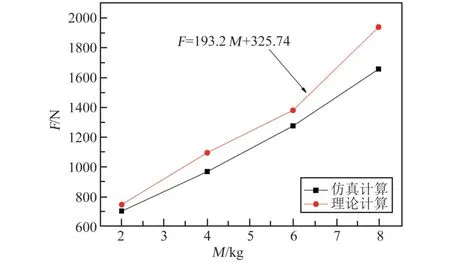
图15 峰值轴向力对比图(仿真与理论）Fig.15 Comparison chart of peak axial force (simulation and theory）

5 结论

1)基于岩土力学理论建立的理论模型，可反映出足垫冲击月壤的运动特性及力学特性，与离散元仿真相比，两者误差在15%以内。

2)理论模型与离散元相比，月壤刚度较大，因此与离散元仿真相比，其侵入深度较小，峰值轴向力较大。

3)足垫侵入月壤深度、着陆过程中峰值轴向力与足垫着陆速度正相关。 侵入深度与足垫冲击速度近似线性，峰值轴向力用多项式进行拟合，便于快速得到其它冲击速度下足垫的动力学响应；冲击加载时间与着陆速度负相关。 因此后续在着陆器月面着陆过程中，应依靠反推发动机等控制方式，降低着陆速度以降低着陆过载。

4)着陆过程中峰值轴向力、冲击时间以及侵入深度与足垫着陆质量正相关，峰值过载与着陆器质量负相关。 因此后续在着陆器月面着陆过程中，应采用结构优化设计，降低着陆质量，缩短着陆器着陆稳定时间，降低冲击力。

参考文献(References）

[ 1] 曾福明， 杨建中， 朱汪，等. 月球着陆器着陆缓冲性能研究[J]. 航天器工程， 2010，19(5)：43-49.

Zeng F M， Yang J Z， Zhu W， et al. Research on landing impact attenuation performance of lunar lander[J]. Spacecraft Engineering， 2010，19(5)：43-49.(in Chinese)

[ 2] 蒋万松， 黄伟， 沈祖炜，等. 月球探测器软着陆动力学仿真[J]. 宇航学报， 2011， 32(3)：462-469.

Jiang W S， Huang W， Shen Z W， et al. Soft landing dynamics simulation for lunar explorer[J]. Journal of Astronautics 2011，32 (3)：462-469.(in Chinese)

[ 3] 陈金宝， 万峻麟， 成玫，等. 深空探测着陆器着陆冲击动力学相似技术研究[J]. 振动工程学报， 2015， 28(6)：871-878.

Chen J B，Wan J L，Cheng M，et al. Research of dynamics similarity technology in planetary landing[J]. Journal of Vibration Engineering， 2015，28 (6)：871-878.(in Chinese)

1.1 危害特点：主要危害心叶、嫩芽。被害叶形成许多细密而长形的灰白色斑纹，使叶子下垂，严重时扭曲、变黄枯萎。有时还会传播植物病毒。

[ 4] 万峻麟， 聂宏， 李立春，等. 基于瞬态动力学方法的月球探测器软着陆腿着陆冲击性能分析[J]. 兵工学报， 2010，31(5)：567-573.

Wan J L，Nie H，Li L C，et al. Analysis of the landing impact performance for lunar landing leg with transient dynamic method[J]. Acta Armamentarii，2010，31(5)：567-573.(in Chinese)

[ 5] 梁东平， 柴洪友. 着陆冲击仿真月壤本构模型及有限元建模[J]. 航天器工程， 2012，21(1)：18-24.

Liang D P，Chai H Y. Lunar soil constitutive model and finite element modeling for landing impact simulation[J]. Spacecraft Engineering， 2012，21(1)：18-24.(in Chinese)

[ 6] 邹猛， 李建桥， 贾阳，等. 月壤静力学特性的离散元模拟[J]. 吉林大学学报：工学版， 2008，38(2)：383-387.

Zou M， Li J Q， Jia Y， et al. Statics characteristics of lunar soil by DEM simulation[J]. Journal of Jilin University：Engineering and Technology Edition， 2008， 38(2)：383-387.(in Chinese)

[ 7] 钱家欢， 殷宗泽. 土工原理与计算[M]. 北京：中国水利水电出版社， 1996：252-254.

[ 8] 郭见扬. 强夯夯锤的冲击力问题(强夯加固机理探讨之一)[J]. 土工基础， 1996，10(2)：36-37.

Guo J Y. The investigation of impact force of dynamic rammer[J]. Soil Engineering and Foundation， 1996，10(2)：36-37.(in Chinese)

[ 9] 高有斌， 刘汉龙， 张敏霞，等. 强夯加固地基的土体竖向位移计算方法研究[J]. 岩土力学， 2010，31(8)：323-328.

Gao Y B， Liu H L， Zhang M X， et al. Simplified calculation method of soil vertical displacement under dynamic compaction[J]. Rock and Soil Mechanics，2010，31(8)：323-328.(in Chinese)

[10] 牛志荣，杨桂通. 强夯作用下土体动力特性研究[J]. 工程力学， 2006，23(3)：118-125.

Niu Z R，Yang G T. Dynamic characteristics of soils during and after dynamic consolidation[J]. Engineering Mechanics，2006，23(3)：118-125.(in Chinese)

[11] 钟世英. 模拟月壤力学特性及软着陆足垫动力响应研究[D]. 杭州：浙江大学， 2012.

Zhong S Y. The Study on Mechanical Properties of Simulated Lunar Soil and Dynamic Response of Soft Landing Footpad[D]. Hangzhou： Zhejiang University，2012.(in Chinese)

[12] 贝克M G.地面-车辆系统导论[M].《地面-车辆系统导论》翻译组，译.北京：机械工业出版社，1978：126-128.

Bekke M G.Introduction to Ground Vehicle System [M]. Introduction to Ground Vehicle System Translation Team， translated. Beijing： Mechanical Industry Press，1978：126-128.(in Chinese)

[13] Oravec H A， Zeng X， Asnani V M. Design and characterization of GRC-1： A soil for lunar terramechanics testing in Earth-ambient conditions[J]. Journal of Terramechanics，2010， 47(6)： 361-377.

[14] Zou M，Jian Q Li，Liu G M，et al. Experimental study of terramechanics characters of simulant lunar soil[J]. Rock ＆ Soil Mechanics， 2011， 32(4)：1057-1061.

[15] Willman B M， Boles W W， Mckay D S， et al. Properties of lunar soil simulant JSC-1[J]. International Journal of Rock Mechanics ＆ Mining Science ＆ Geomechanics Abstracts，1995， 33(1)：13A.

[16] Oravec H A. Understanding Mechanical Behavior of Lunar Soils for the Study of Vehicle Mobility[D]. Krylov：Case Western Reserve University， 2009.

[17] French B M， Heiken G， Vaniman D， et al. Lunar sourcebook： ausers guide to the Moon[J]. Sky ＆ Telescope，1991，254：56-62.