精解·探规·寻根·迁移：数学教师研题的四重境界

【摘 要】研究习题是高中数学教师的基本教学任务，也是必备素养与能力。教师研题有四重境界：第一，多思精解，比较不同解法的效率差异;第二，探求规律，理解试题内在的本质属性;第三，探寻题根，挖掘试题背后的命题思路;第四，有效迁移，开发试题蕴含的教学价值。

【关键词】高中数学;多思精解;探求规律;探寻题根;有效迁移

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2020）91-0033-05

【作者简介】曾荣，江苏省南通市教育科学研究院（江苏南通，226001）数学教研员，正高级教师，江苏省特级教师。

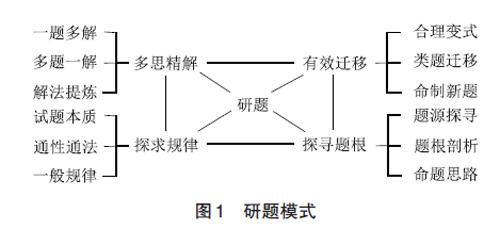
习题是课堂教学内容的巩固与深化，应当为学生发展数学学科核心素养提供助力。优质的数学习题教学，有利于帮助学生理解数学知识的本质，感悟数学的基本思想，积累数学思维的经验，提升数学学科核心素养。研究习题是高中数学教师的基本教学任务，也是他们的必备素养与能力。笔者认为，教师研究习题，不能局限于会解、能讲，而应该依托优秀的试题，追求更高境界——多思精解、探求规律、探寻题根、有效迁移。教师研题的基本模式如图1所示。本文结合江苏省南通市2020年高三第一次模拟考试第17题谈谈教师研题的四重境界。

一、第一重境界：多思精解，比较不同解法的效率差异

教师研题的基础是解题，用合适的方法、广阔的思维进行解题，要善于进行一题多解、多题一解、解法提炼。一道优秀的试题往往讲究解法的多样性和不同解法效率的差异性，这种差异性体现出解题人思维品质和数学素养的差异。教师研题时要从学生能力基础、知识本质体现、思想方法渗透等多角度进行思考，探求不同的解法，深入比较不同解法效率的差异性。在精解一道题的基础上，教师要善于举一反三，向解一类题、一组题方向发展。

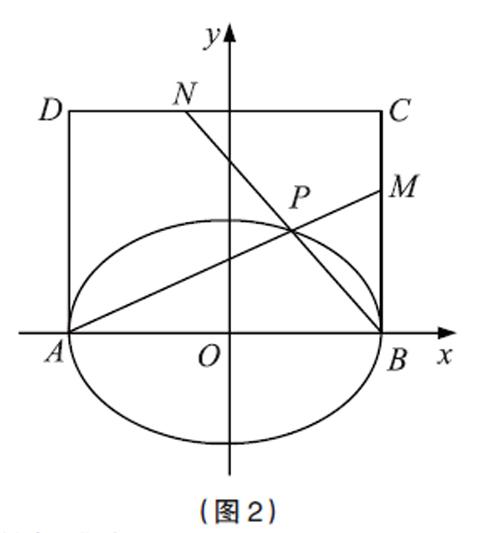
题1（南通市2020年高三一模第17题）：如图2，在平面直角坐标系xOy中，椭圆E： [x2a2] + [y2b2]=1（a>b>0）的焦距为4，两条准线间的距离为8，A，B分别为椭圆的左、右顶点。

（1）求椭圆E的标准方程;

（2）已知图中四边形ABCD是矩形，且BC=4，点M，N分别在边BC，CD上，AM与BN相交于第一象限内的点P。

① 若M，N分别是BC，CD的中点，证明：点P在椭圆E上;

② 若点P在椭圆E上，证明：[BMCN]为定值，并求出该定值。

【思路分析1】第②问是一个“动中求定”的问题，在动态图形中研究定值问题。对于这样的图形，我们要思考图形因何而动，图形中的动态元素之间存在怎样的联系，因为动因决定了运算对象。本题如果理解为点P运动而引起直线AP，BP运动，从而导致整个图形在运动，那么我们不妨从设点P（x0，y0）开始。

【運算路径1-1】

设点P（x0，y0）[?KAP?AP?yM?BM][?KBP?BP?xN?CN] ? [BMCN]（用x0，y0表示）[P在随圆上]求出定值。

【相似思路】考虑到点P为椭圆上的点，我们也可以通过三角换元的方式设出点P的坐标为P（2[2cosθ]，2sin[θ]）。这种做法，运算的路径和原来基本一致，但变量从两个变为一个，便于学生实际操作。

【运算路径1-2】

设点P（2[2cosθ]，2sin[θ]）

[?KAP?AP?yM?BM][?KBP?BP?xN?CN] ? [BMCN]（用[θ]表示）?求出定值。

【思路分析2】如果把点P理解为AP与BP的交点，因为直线AP与BP运动导致点P跟着运动，从而导致整个图形在运动，那么我们不妨从设AP与BP的方程开始进行运算。

【运算路径2】

[设点AP的方程：y=k1（x+2[2]）?yM?BM][设点AP的方程：y=k1（x+2[2]）?xN?CN][ [BMCN]（用k1，k2表示）][?k1·k2= - [b2a2] = - [12]][?求出定值。]

【思路分析3】从研究的目标出发，将BM和CN分别利用点M的纵坐标和点N的横坐标表示，故可以从设点M的和点N的坐标开始运算。

【运算路径3】

【比较反思】 以上几种方法是解析几何中的常见解法，但不同解法的效率有明显差异。在同一数学情境中，不同的运算思路、运算程序的设定，体现了一定的规划设计能力。对于具体的数学运算，我们要善于结合运算情境，深刻理解运算对象的特征，挖掘其内涵。只有以数学思维为基础进行规划设计，运算能力的提升才能得到有效的落实。

二、第二重境界：探求规律，理解试题内在的本质属性

多思精解，深入比较不同解法的效益差异，可以帮助师生优化解题路径，提升学科素养。同时，我们应该依托试题，探求其内在规律，理解试题内在的本质属性。在深入研究多种解法的基础上，我们应进一步思考，问题背后的知识本质是怎样的？解题方法蕴含着怎样的通性通法、数学思想？是否存在更一般的规律？为什么会有这样的规律？对题1，我们进行如下思考：

【思考1】题1依托矩形这一背景，研究了与椭圆有关的问题。第①问是给定了两个特殊的分点，研究了对应的直线的交点在椭圆上。如果不是中点，而是三等分点、四等分点，……，n等分点呢？有没有更一般的结论呢？

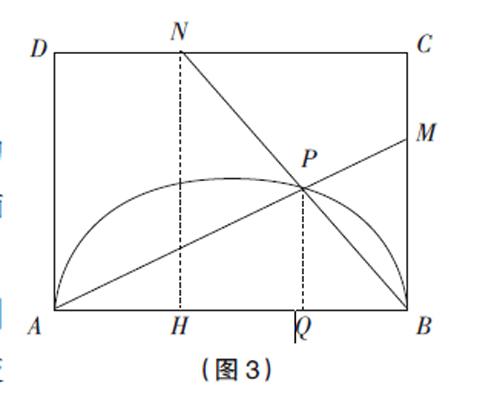
【规律1】如图3，在矩形ABCD中，M，N分别在边BC，CD上，且[BMBC] = [CNCD]，则AM，BN的交点在一个椭圆上。

【思考2】规律1中的交点形成的轨迹能形成一个完整的椭圆吗？如何才能形成一个完整的椭圆？

【规律2】如图4，在规律1的基础上利用对称性，可以形成一个完整的椭圆。

【思考3】第②问中，已知点P在一个特殊的椭圆上，可证[BMCN]为定值。若对于任意的椭圆 [x2a2] + [y2b2]=1（a>b>0），[BMCN]仍为定值吗？

【规律3】如图5，在平面直角坐标系xOy中，A，B分别为椭圆E： [x2a2] + [y2b2]=1（a>b>0）的左、右顶点。已知图中四边形ABCD是矩形，点M，N分别在边BC，CD上，AM与BN相交于第一象限内的点P。若点P在椭圆E上，则[BMCN] = [ba]。（证明方法可参考题1第②问）

三、第三重境界：探寻题根，挖掘试题背后的命题思路

对于一道试题，教师若能多思精解、由特殊到一般、把握本质属性、研透内在规律，已属不易。然而，优秀的教师往往不止于此，他们会研究问题出处，探寻题根，并深刻挖掘基于题根的命题思路。这种基于“问题从哪里来？怎么演变过来的？命题者的命题思路和方法是怎样的？”的思考，力求站在命题者的视角审视问题，求本归真，更有利于提升师生的数学学科素养。本题题根如下——

题2（苏教版高中数学选修2-1 P38第14题）：把矩形的各边n等分，如图6连结直线，判断对应直线的交点是否在一个椭圆上？

【题根分析】本题依托矩形这个载体，通过等分的方式产生了有限个点。等分的实质是“成比例”，通过“成比例”可以将“有限”转化为“无限”，由此进一步通过对应直线相交的方式产生的无数个点。研究这些点的特征，实质上是研究动点的轨迹问题。

【命题思路】在高考、模考中如果直接考查轨迹问题，那么对学生的学习要求高、难度大。为了让问题能更加适合于考查学生，命题者通过“特殊化”和“逆向思考”的方式改变了问题的呈现方式，使试题源于教材，但不拘泥于教材。

（1）特殊化：在题1第①问中，命题者将分点特殊化，取其中一个特殊的分点进行研究。因为只取了一个点，就不再是对轨迹问题的研究了。命题者结合具体数据，给出特殊的椭圆，将求椭圆轨迹问题转化为求在特定椭圆上的特殊点。这样，动态问题转化为静态问题，大幅度降低了难度，适合用于考查学生。

（2）逆向思考：满足某一特征的点在曲线上，曲线上的点都满足某一特征，这是解析几何研究的两个主要问题。题1第①问研究的目标是点在曲线上。命题者在命制第②问时，通过逆向思考，告知曲线上的一个动点，进而研究相关点的几何特征。在这个“动”的情境中，可以通过不同的引参方案，考查学生的思维能力和数学运算素养。

四、第四重境界：有效迁移，开发试题蕴含的教学价值

教师研题不仅仅是为了提升自身的数学素养，更重要的是为了开发试题蕴含的教学价值，帮助学生提高数学解题能力，加深对数学的理解。教师将自己解题、探规、寻根的经历转化为一种探究活动，可以帮助學生实现对问题的再发现、再解决。同时，在教学中，教师还要善于有效迁移，对试题进行改编、变式、拓展，举一反三，让学生在迁移、深化中体悟数学的本质和数学的系统性、结构性，感悟数学的统一之美、变化之美。

迁移1 （苏教版高中数学选修2-1 P48第16题）：如图7，在矩形ABB'A'中，把边AB分成n等份。在边B'B的延长线上，以BB'的n分之一为单位连续取点。过边AB上各个分点和A'作直线，过B'B延长线上的对应分点和点A作直线，这两条直线的交点为P，P在什么曲线上运动？

迁移2 （苏教版高中数学选修2-1 P54第13题）： （阅读题）在工程中，画拱宽为2a，拱高为h的抛物线，常用下面的画法：

（1）作矩形ABCD，使AB=2a，DA=h;

（2）分别取CD，AB的中点O，H，把线段DA，OD，HA各n等分;

（3）如图8连线得到各交点，将交点连成光滑曲线，就得到抛物线的一半;

（4）用同样方法画出另一半。

你能说明上述画法的正确性吗？

对于以上问题，我们要在外在形式、结构的一致性的基础上，深刻认识本质的一致性。

【思考1】你能研透上述题2、迁移1、迁移2的本质一致性吗？（椭圆、双曲线、抛物线统称为圆锥曲线。圆锥曲线在定义的方式、知识的结构、研究的方法等方面具有一致性。设计这样的问题，意在引领学生举一反三，由表及里，深刻认识圆锥曲线的本质。）

【思考2】你能参考题1的改编方式，将迁移1、迁移2改编成形如题1的考题吗？（在深刻认识问题本质的同时，教师也要学会“再创造”，借鉴优秀试题的命制方式，“再创造”出更多的优秀试题，让学生有机会再练、再悟、再提高。）

数学家波利亚曾指出：“解题是人类最富有特征的一种智力活动。”作为数学教育工作者，我们不能仅仅满足于一般意义上的解题，我们要善于深度研题。通过“多思精解—探求规律—探寻题根—有效迁移”的路径，使得研题活动助力教师的专业成长，助力智慧课堂的有效达成，也助力促进学生核心素养的不断提升。

【参考文献】

[1]教育部.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社，2018.

[2]曾荣.优化解题路径  提升运算素养——以解析几何为例谈数学运算素养的培养[J].教学月刊·中学版：教学参考，2019（4）：46-50.

[3]曾荣.命题视角下的习题教学——以《应用基本不等式求最值》一课为例[J].教育研究与评论：中学教育教学，2017（2）：89-92.