改进遗传算法求解订单分批优化模型

冯爱兰，王晨西，孔继利

1.北京科技大学 机械工程学院，北京100083

2.北京邮电大学 现代邮政学院，北京100876

1 引言

目前，网上零售发展迅速，它给人们带来极大便利的同时，也给电商配送中心带来了巨大的挑战。配送中心订单呈现出小批量、多品种的特征，拆零拣选成为其主要的业务形态。这种业务形态下需要的劳动量更大，劳动程度更密集，因此，提高拣选作业效率极其重要。

在电商配送中心内部，通常将存储区和拣选区分开以提高运营效率。在拣选区内，往往根据货品的拣选频率设置不同的拣选区。拣选频率较低的商品存放在普通隔板货架区进行拣选，拣选频率较高的货品则存放在流利式货架区进行拣选。流利式货架扩展性好，拣选效率高，出错率低，单个SKU 存放数量较多，且补货不影响拣货流程，因此得到了广泛的应用。但在实际拣选中，流利式货架拣选策略大多依据管理者经验，或引用普通隔板货架适用的策略，导致拣货员等待时间过长，拣选效率不高。

流利式货架分区拣选系统，如图1 所示，由于其拣选效率高，分区管理方便，责任便于追踪，拣货员易于熟悉自己的拣选区域，广泛应用于快速拣选区内周转频率较高货品的拣选。van Gils T 等人[1]讨论了订单分批、储位指派、路径策略、分区拣选之间的关系，通过实验证明仓库在考虑同时采用这四项策略时，将可以获得显著的收益。优化流利式货架分区拣选系统的订单分批方法和储位指派策略将会使拣选效率得到进一步提升。学者李诗珍[2]通过仿真研究得出：订单分批策略对减少拣货作业的总时间影响最大。至今，对拣选系统中订单分批方式、模型及求解算法的研究依然是热点。目前主要的订单分批方式有时窗分批、单品合计量分批、固定订单量分批、智能型分批等。

图1 流利式货架分区拣选系统场景

从订单分批模型来看，大多学者根据研究场景和优化目标的不同建立数学模型。王占磊[3]考虑双区型仓库中以总拣选距离最短为目标，以多个拣选设备并存为条件建立优化模型。赵兰[4]以拣选总行走时间与分拣时间之和为优化目标，对分批模型和求解算法进行仿真实验，并分析了订单数量、批次容量等参数对优化目标的影响。马飞[5]考虑路径相似度，以分批后所有批次的总相似程度最大为目标建立数学模型。王转等人[6]基于电商配送中心人到货整箱拣选系统，考虑拣选器具和商品包装体积，构造了以最大化里程节约量为目标的订单分批模型。王旭坪等人[7]考虑订单完成期限，建立以最小化平均有效订单服务时间为目标的订单分批模型。Jiang Xiaowei[8]考虑带缓存区的订单分批及任务释放顺序问题，建立以总作业时间最短为目标的订单分批模型。

在模型求解方法上，大多学者考虑相似度规则，设计启发式算法来求解。订单分批问题是NP 难问题，精确算法难以适应实际拣选系统，目前主要有种子算法、节约算法、数据挖掘算法、智能算法等。Tseng 等[9]研究了两种不同拣选路径规则下的9 种种子选取规则和10种订单添加规则的表现。Lam 等[10]给订单设置优先规则，根据优先级顺序再考虑拣货箱约束，进行订单合并分批。魏伟[11]利用节约算法进行订单路径计算并设计遗传算法求解以最短路径为目标的数学模型，最后通过仿真验证其有效性。马飞[5]用数据挖掘中的系统聚类分析方法求解订单分批模型。吴天行[12]引入“反学习”概念，对传统的蜂群算法加以改进，提升求解订单分批算法的性能。Xiang Xi 等[13]用变邻域搜索算法求解了其提出的订单分批模型。邵泽熠等[14]针对传统K-均值算法中K 值人为确定造成聚类结果误差大的缺点，采用密度和最小距离综合最优指标确定多个初始聚类中心，并运用改进遗传K-均值算法确定最优分批数量，进行订单分批优化。Hong S等人[15]考虑了流利式货架拣选系统中的拥堵问题，建立订单分批模型对系统中的等待时间进行了优化。

学者对订单分批的研究多考虑拣货员的拣选时间及拣货路径的因素，忽略了任务在系统中的滞留给订单响应速度带来的影响。在流利式货架分区拣选系统中，任务在系统中的滞留会延长订单响应速度，并且给缓存区造成一定压力，进而增加拣选系统的空间成本。

学者对储位指派策略的研究，忽略了货架高低对拣货员拣取带来的影响，当货品存放至不同层数时，会导致不同的拣取时间，当订单行数增加时，可以优化的空间非常大。Petersen 等人[16]比较了分类存储和随机存储，考虑了类的数量，发现分类存储比随机存储节约拣货员的行走时间。李晓春[17]研究了流利式货架分区拣选系统中，在拣货员拣货速度不同的情况下，通过对品项在各分区间储位的安排以平衡各分区拣货员的作业量，提出了储位指派算法。但在电商背景下，商品变化比较频繁，商品周转率易随季节变动，定位存储的管理成本较大。

在分区拣选系统中，拣货员之间互相影响，订单分批问题不仅要考虑订单分批结果，还要考虑分批后的任务释放顺序。相同的订单分批结果，当任务释放顺序不同时，系统的处理效率会有很大差异。流利式货架作为快速拣选区的常用货架，提升仓库整体拣货效率和订单响应速度非常重要。由于其布局的特殊性，无需考虑路径带来的影响，普通货架中的订单分批策略是否适应流利式货架值得讨论。

本文考虑流利式货架分区拣选系统中相邻区域互相影响的特点，考虑减少相邻区域作业时间的差值（Minimize the sum of the differences of working time between any adjacent areas）以减少拣货员在交接处的等待时间和货物在系统中的滞留时间，以所有相邻区域作业时间差值之和最小和订单分批数量最小为目标，建立多目标规划数学模型，此模型用MSD 表示，并用改进的遗传算法求解订单分批结果及任务释放顺序，对流利式货架分区拣选系统进行优化。

在储位指派方式上，本文从拣货员拣取的便捷性出发，将周转频率较高的货品存放至流利式货架中拣货员最容易拣取的层数，以减少总体拣货时间，提出分类随机指派策略。

2 问题描述

流利式货架分区拣选系统就是将流利式货架划分出多个拣选区域进行作业，相邻区域处设置有缓存区，在整个拣选过程中，各个拣选区域大小保持不变的拣选系统。由于不等分区在实际场景中应用较少，且分区方案受多种因素影响，本文将研究场景设定为随机存储下的等分区接力式拣选系统，对于不等分区拣选系统，本文研究方法同样适用。

流利式货架分区拣选系统中，分区大小相同，且在拣选过程中大小不变，每个区内有一名拣货员，每个拣货员负责相应区域的拣选作业，如图2 所示，拣选作业方向从左至右，区域2 的拣货员相对于区域1 为下游拣货员，相对于区域3 为上游拣货员，相邻区域交接处设有交接缓存区（Interface buffer）。每一名拣货员从左侧缓存区或任务释放端领取任务，推着拣货箱（Container）拣完相应区域的任务后，将拣货箱放至下游的缓存区或任务完成端，之后空手返回上游的缓存区领取新任务，如果缓存区无待拣选任务则静止等待，直到有任务出现。每个拣货员配有手持终端，任务开始时，手持终端扫描箱子上的二维码，提取任务，任务完成后，再次扫描二维码，确认完成当前区域的任务。

系统中涉及到的时间如下：

任务开始时间：每个区域的拣货员开始新任务，完成手持终端与拣货箱任务绑定工作的时间，即拣选前的准备工作时间；

拣选时间：拣货员读取任务，寻找待拣选商品，拣取商品放至拣货箱的时间；

前进行走时间：拣货员在有拣选任务时，在所负责区域内推着拣货箱向下游前进的时间；

任务完成时间：拣货员完成任务后，将拣货箱放至缓存区，并进行设备操作的时间；

返回行走时间：拣货员空手返回至上游缓存区的时间；

等待时间：拣货员返回至上游缓存区时，没有待拣选任务，进而静止等待的时间；

作业时间：拣货员开始任务到完成任务返回出发点的所有时间，即工作时间。

在串行拣选中，同一个任务依次进入每个拣选区域，不同区域每个人拣选的任务是不一样的，每个任务经过每个区域都会产生任务开始时间、拣选时间、前行行走时间、任务完成时间和返回行走时间，即当前任务在当前区域的作业时间。拣货员在系统中的等待和货物在系统中的滞留时间几乎不可避免，不仅造成了时间的浪费，也会造成拣货员工作负荷的不平衡，如何减小所有拣货员完成任务的总时间，减少人员在交接处的等待消耗以提高系统效率，降低人员成本，是管理者迫切需要解决的问题；如何降低任务在系统中的滞留时间以缩短任务的履行时间，提高订单响应速度，是提高顾客满意度的迫切需要。

3 模型构建

3.1 模型假设

基于对流利式货架分区拣选系统的作业特点分析，模型假设如下：

（1）货架中储位大小相同，且同种商品只存在货架一处；

（2）拣货员的任务熟练程度相同，由于每层货架拣选的便捷程度不同，每层货物的拣取时间不同；

（3）拣货员的拣货行走速度和空手行走速度视为相同且恒定，忽略加速时间和减速时间；

（4）货品补充及时，不会缺货；

（5）拣货员一次拣取动作只拣取一个订单中一个品项；

（6）每个订单中每种SKU数量为1；

（7）订单不能分割，也不能插单；

（8）每个订单中所含商品的总体积不超过拣货箱容积；流利式货架拣选的订单非顾客原始订单，当待拣选订单总体积超过拣货箱容积时，订单不再进行分批；

（9）不超过拣货箱最大容积限制的任务都可以放进拣货箱进行拣选，本文忽略商品的形状及三维，在设置拣货箱容积时，会考虑将最大拣货箱容积限制的设定数值小于拣货箱的实际容积。

图2 分区拣选系统作业过程示意图

模型参量如下：

I 表示订单总数，i=1,2,…,I ；

B 表示流利式货架分区数量，z=1,2,…,B；

m 表示货架层数；

nz表示第z 区最后一列的编号，n0=0；

f 表示拣货位编号，图3是一个m 为4的货位编号顺序；

Vmax表示拣选设备最大容量；

Vf表示第f 个储位处所存取商品的单位体积；

PTzj表示第z 个区内的拣货员拣选第j 批任务的拣选时间；

ptf表示第f 个储位处所存取商品的单位拣选时间；

决策变量如下：

J 表示订单合并批次数量，j=1,2,…,J ；

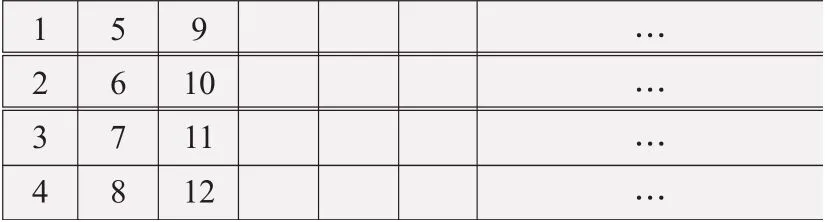
图3 流利式货架储位编号顺序

3.2 模型建立

在流利式货架中，人员的总行走时间与所有任务的路径长度和速度相关，速度相同且恒定的情况下，减小任务数量可以缩减人员行走时间；减小相邻区域作业时间的差值可以缩减人员在系统中的等待时间或货物在系统中的滞留时间，以此缩减完成任务的总时间，提高系统效率。所以，本文以相邻区域作业时间差值之和最小和订单分批数量最小为目标，建立流利式货架分区拣选系统的数学模型。

Objective：

Subject to：

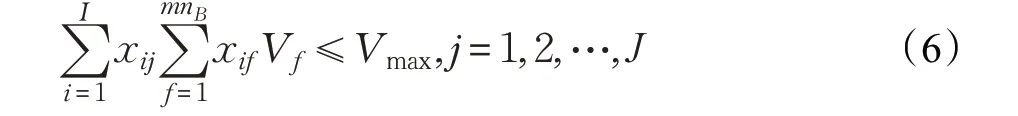
式（1）为最小化分批数量；式（2）为最小化所有相邻区域作业时间差值的和，由于相邻区域的任务开始时间、前行行走时间、任务完成时间和返回行走时间相同，故在公式中相互抵消；式（3）为J 的取值范围；式（4）为第z 个区的拣货员拣选第j 批任务的拣货时间；式（5）表示一个订单只能分到一个批次里，即订单不能分割；式（6）为拣货箱的容量约束，每一个拣货任务中商品的总体积不能超过拣货箱最大容量。约束（6）保证了目标函数（1）在最小化的过程中不会出现不可行解。这是一个多目标0-1整数规划模型。

3.3 问题特点

本文提出的订单分批模型与一般的订单分批问题相比，有以下特点：

（1）两个目标的处理问题。在模型中，目标2 是( J-1) ×( B-1) 个差值的和，所以目标1 中J 的最小化将体现在目标2 中，两者不是独立的两个目标。因此，在求解过程中如何处理两个目标之间的关系直接影响解的收敛过程。求解多目标问题的方法主要有：主要目标法、统一目标法、分层序列法、Pareto 法等。本文中，由于两个目标有相关性，量级也不同，较难判定权重，难以归一化处理，且一个目标在另一个目标中有所体现，因此考虑对两个目标设置优先级，用分层序列法求解。分层序列法首先根据目标的重要程度进行排序，每次都在前一目标的最优解内，寻找下一目标的最优解，直到最后求出共同的最优解。订单分批数量J 会直接影响拣货员的行走距离，进而影响总完成时间，所以优先目标1，在目标1每次达到最优的情况下，寻找令目标2差值之和最小的个体。

（2）解的结构复杂。流利式货架分区拣选系统中，相邻拣货员的作业时间差值会影响货物在系统中的滞留和拣货员在系统中的等待，因此订单分批之后的任务释放顺序非常重要。订单分批结果及任务释放顺序都会影响目标2 差值的大小，在算法求解过程中，既要得到订单分批结果，又要得到任务释放顺序。

（3）模型目标对优化指标的客观反映。本文的目标是最小化分批数量和最小化相邻区域的作业时间差值，两者都不直接是反映仓库拣货效率及订单响应度的指标，但是通过减少作业时间的差值可以缩小拣货员的作业总完成时间和任务的平均履行周期。

4 求解MSD模型的改进遗传算法

这种场景下的订单分批问题，类似于多目标装箱问题，除了考虑使用的箱子数最小，还要考虑缩短相邻区域作业时间差值。从文献来看，研究多目标装箱问题的文献不多，可参考的算法较少。但是遗传算法在订单分批问题的研究中应用广泛，充分证明了它在解决订单分批问题上的可行性，且遗传算法有很强的全局搜索能力和较强的鲁棒性，所以本文设计了遗传算法求解所提出的MSD订单分批数学模型。

4.1 个体编码及解码方式

采用实数编码方式，订单数为I ，则染色体为I 以内整数的随机排列。考虑拣货箱容积限制，按排列顺序进行分批。用一个实例来表述：假设订单个数为20，每个订单都可计算出其商品总体积，订单编号为1到20之间的整数，则染色体编码为20以内整数的随机排列，如图4所示，图中第一行为一个染色体排列。

解码过程如下：按照染色体排列，根据图4 第二行中每个订单对应的商品总体积。将货品依次进行分批，当待分批订单不能加入到当前批次时，此订单成为一个新的批次，不限定订单的批次数。假设拣货箱容积为15，计算此染色体所需分批次数。订单18 为第一个批次，订单8的体积加上订单18大于15，所以不能分入一批，订单8 为第二批，订单14 的体积4.87 加上7.76 小于15，则订单14与订单8为第2批，订单6的体积4.36加上4.87，再加上7.76 大于15，则订单6 为第3 批，依次对每个订单进行分批，得到订单分批结果及任务释放顺序，如图5所示，案例共分11批。

这种编码方式下，任意产生一组排列都是可行解，一组排列对应一种订单分批结果和任务释放顺序，有效解空间为I!。

初始种群生成采用随机生成的方式，随机生成一定数量的染色体，每个染色体是I 以内整数的随机排列。

许多算法中采用的限定产生特定批次数的编码方式，会产生不可行解，并且会引导种群向每批任务拣货箱容积利用率高的方向进化，忽略了任务释放顺序的优化及接力式拣选系统的特点。本文采用的编码方式，虽然初始随机产生的染色体对应的订单分批数量较多，但是多数染色体对应的每批任务总体积相差较小，这样就会在遗传过程中很好地利用任务均衡性的优点，以减少差值。同时，目标函数中最小化订单分批次数的目标也会引导种群向拣货箱容积利用率高的方向进化。

4.2 适应度函数

适应度函数在算法设计中，直接影响算法的进化方向和解的质量。本文的多目标问题采用分层序列法求解订单分批结果及任务释放顺序，由于目标2为最小化( J-1) ×( B-1) 个相邻区域作业时间差值的和k（时间以秒为单位，k 为大于1的整数），每个差值和J 的缩小都会降低总差值k，因此优先目标1，在目标1每次达到最小的情况下，寻找目标2的最优解。为了保留k 较小个体的优秀基因结构，又保证J 向最小化的方向进化，设计了以下适应度函数。

步骤1 计算所有待分批订单的商品总体积，除以拣货箱的最大容积Vmax，向上取整得到这批订单所需的理论最小分批数量Jmin。

步骤2 计算每个染色体所需的订单分批数量J 、订单分批结果及任务释放顺序，方法如4.1节中介绍，案例中J=11，订单分批结果及任务释放顺序如图5。

步骤3 通过订单分批结果及任务释放顺序计算每个染色体对应的所有相邻区域作业时间差值，再求和得到k。

步骤4 适应度计算公式如式（7）所示：

将订单分批数量J 放在指数位置，将差值k 放在底数位置，这样当适应度比较时，J 较小的染色体会占据主要优势，被选择的几率更大。当k 相同时，会优先选择J 较小的个体，J 相同时，会优先选择k 小的个体。这样在选择过程中，优先了目标1，便于在目标1最小的情况下，寻找k 最小的个体，也给k 较小但是J 没有达到最小的个体进化空间，保留其令k 值小的优秀基因结构，使得算法在向拣货箱容积利用率高的方向进化。

4.3 选择策略

遗传算法中，根据适应度值对每个个体进行操作。遵循“适者生存”的原则，适应度越高的个体，越容易被选中进入下一代。

本文结合精英保留策略和轮盘赌的方法作为新的选择策略。先用轮盘赌的方法选出交叉个体进行交叉；经过交叉与变异之后，再进行精英保留策略；父代和子代分别通过适应度排序，选取父代x%的优秀个体和子代的优秀个体组成新的种群，即用父代x%的优秀个体替换掉子代相同数量的较差个体。

这样优秀个体也可以参与交叉、变异，为产生更优秀的基因结构提供可能，也可以在组成新的种群时保留历史最优个体，使算法尽快收敛。

4.4 交叉算子

轮盘赌的选择操作完成之后，算法通过交叉算子产生新的个体。交叉是形成新个体的重要步骤，也是遗传算法不同于其他进化算法的重要特征。

图4 订单数量为20的一组订单排列及对应的商品总体积

图5 订单分批结果及任务释放顺序

通过编码方式可知，一个解内部整数的顺序调整可以变化订单分批方式和任务释放顺序，每个整数是不能重复的且不可遗漏的，基于此考虑采用基于映射的交叉方式，随机选择两个点，两个切入点之内的部分保留，并形成映射关系，将两端与其相同的基因替换为形成映射关系的基因。由于在交叉变异之后还会有父代的精英保留操作，所以交叉概率设置为1，以增强群体中新结构的引入，也不用担心改良基因的丢失速度。在交叉过程中，随机选择交叉点和中间段的交叉长度。

例如，图6为两条染色体，随机选择两个交叉点，假定选取第4与第5个基因之间为第一个交叉点，第11与第12 个基因之间为第二个交叉点，两个交叉点将每个染色体分成三段，如图7所示；形成三对映射关系：（11，4，10，12，14）；（18，6）；（9，2）；经过映射变换后新的染色体如图8所示。

图6 交叉前的染色体

图7 取交叉点后的染色体

图8 交叉完的染色体

4.5 变异算子

变异操作是指通过改变染色体本身的基因值来生成新的个体，给个体增添新的基因结构，提高了群体多样性，可以提高算法的局部搜索能力，有效地避免算法的早熟现象，是遗传算法中非常重要的步骤。

根据解的特点，采用随机两点变异，也就是交换变异。参与变异的个体数等于种群大小乘以交叉概率，每个待变异个体随机选择两个点进行交换，形成新的个体。如图9所示，第1行是变异前的染色体，将第5个基因和第14个基因交换，形成第二行的新染色体。

图9 变异前的染色体和变异后的染色体

5 实例分析

本文将MSD的订单分批方法与以最小化订单分批数量为目标的单目标分批方法、先到先服务订单分批方法进行对比，验证MSD订单分批方式的优化效果，并将改进的遗传算法与基于节约原则的种子算法对比，验证改进遗传算法求解MSD方法的效果。

种子算法在订单分批问题中应用广泛，由于本文的研究背景是流利式货架，用基于节约原则的种子算法（Seed algorithm based on saving principle）求解MSD数学模型，选取种子的方法及订单累加原则要考虑流利式货架分区拣选系统的特点。选取种子的方法为：计算每个订单在每个区作业时间的标准差，选择标准差最小的订单作为种子订单；累加订单方式为：节约原则，选取剩余订单池中与种子订单合并后，所有相邻区域作业时间差值之和减小量最大的订单进行累加。种子订单采取不断更新模式，每次并入种子订单都更新种子。在累加过程中，考虑拣货箱最大容积约束，不能再添加订单时，将当前种子作为新的一批任务，重新选取新种子。由于计算差值时，要将所有订单进行分批，因此除去已分批订单，将剩余订单按体积降序排列计算差值之和k 。在算法过程中，加入优秀个体保留原则，每次累加订单，都将当前最优个体与历史个体比较，选取最优个体作为新的历史最优个体，此算法结果用M-SDSP表示。

先到先服务订单分批（First Come First Served）是按订单到达时间先后顺序，考虑拣货设备容积约束进行分批，其灵活性高、简单、快速，可以随时插单，被广泛应用于现实场景中，是一种经典的订单分批方法，其结果用FCFS表示。

以最小化订单分批数量（Minimize Quantity of Order Batching）为目标的模型，类似求解将一定数量的物品放至箱子求最小箱子数量的一维装箱问题，其目标函数为最小化分批数量，考虑拣货箱容积约束和订单不能分割。采用经典的装箱问题算法——降序首次适配算法（First Fit Decreasing）求解，其结果用MQOB表示。

本文提出的以最小化相邻区域作业时间差值之和与最小化订单分批数量为目标的MSD订单分批数学模型，用前一章设计的遗传算法GA 进行求解，其结果用M-GA表示。

基于MATLAB R2015a开发环境，设计实验背景和参数，考虑在不同分区数量下，分析比较不同方法或算法的结果，采用仿真计算的方法求出各种方法下的各指标值，对结果进行比较和分析。

5.1 实验参数与评价指标

流利式货架常用的布局有直线型拣选线和U 型拣选线，本文选取直线型布局进行研究，研究结果对U 型布局同样适用。选用的流利式货架为4 层，在拣选方向，分别等分为3区，4区，5区进行不同场景的实验。图2是分区数量为4的流利式货架布局，储位共有4层，100列，总长50 m，400 个储位即存放400 种SKU，存储方式采用随机存储，储位编号分布如图3所示。

由于流利式货架一般进行拣选频率较高的商品拣选，故将存在货架中的400 种SKU，按拣选频率分成A类，B 类，C 类，种类数占比为1∶1∶2。随机生成10 组订单进行实验，每组订单200 个，每个订单包含1～5 种SKU，每种SKU数量为1件，商品体积都在0.1～6 L之间。

由于拣货员拣取每层货架上货物的便捷程度不同，经查找资料，拣货员拣取的便捷程度从上往下依次是第三层，第二层，第一层，第四层，故本文设置拣货员拣取第一层至第四层中每件商品的时间依次是14 s，12 s，10 s，16 s。

拣货员在拣选时的行走速度为0.5 m/s，返回时的行走速度为1 m/s，每个区域的任务开始时间和任务完成时间为7.5 s，拣货箱最大容量为100 L。

本文提出的MSD订单分批方法考虑缩小拣货员的等待时间和货物的滞留时间，进而缩短所有任务的总完成时间和平均履行周期。因此选取以下指标衡量各方法或算法的表现：

所有任务的完成时间CT ：从0 s开始任务计时，到CT 时所有任务结束，即最后一批任务离开拣选系统的时刻，亦是完成所有拣选任务的时间。

所有任务的平均滞留时间RT ：所有任务在缓存区的滞留时间，当拣货员还未返回至缓存区时，上游拣货员已将任务放至缓存区，货物就会滞留直至下游拣货员返回取走；货物滞留数量影响到交接缓存区的容量，如果滞留货物较多，则需要更多的缓存空间，影响仓库的布局，增加设备和空间成本。

所有任务的平均履行周期FT ：每批任务从进入拣选系统到离开拣选系统的时间为任务的履行周期，计算所有任务履行周期的平均值。

所有拣货员的等待时间之和WT ：所有人完成整个拣选过程中的等待时间，以此来衡量人员的时间浪费。

5.2 实验过程与结果分析

M-SDSP 通过不断选取新种子和累计订单得到订单分批结果及任务释放顺序；FCFS 方式由于订单到达顺序有很大的随机性，故随机生成100 种到达顺序，考虑拣货箱最大容量约束，进行订单分批，得到不同指标结果，求得100种到达顺序下各指标值的平均值。由于订单的商品总体积确定，FFD算法是将订单按商品总体积降序排列，考虑拣货箱容积约束，将待拣选订单依次添加至编号最小的批次里，所以在商品总体积都不相等的情况下，MQOB 方法的结果是一定的。本文提出的M-GA方法，在遗传算法部分，经过多次变换参数，调整遗传算法策略，对比了不同参数下的结果和时间，最终确定遗传算法的参数如下：种群大小为50，交叉概率为1，变异概率为0.3，精英保留数量为父代的20%。算法运行得到满意解，求得满意解的各指标值，每组订单运行10次，求各指标值的平均值。得到满意解后仿真计算求各指标值的方法如图10所示。

计算10组订单的指标值，表1展示了一组订单在不同方法下的各指标值，时间指标均四舍五入为整数。计算每组订单下，M-GA 相对于M-SDSP、FCFS 和MQOB各指标的优化率，取10 组订单各指标优化率的平均值得到表2。

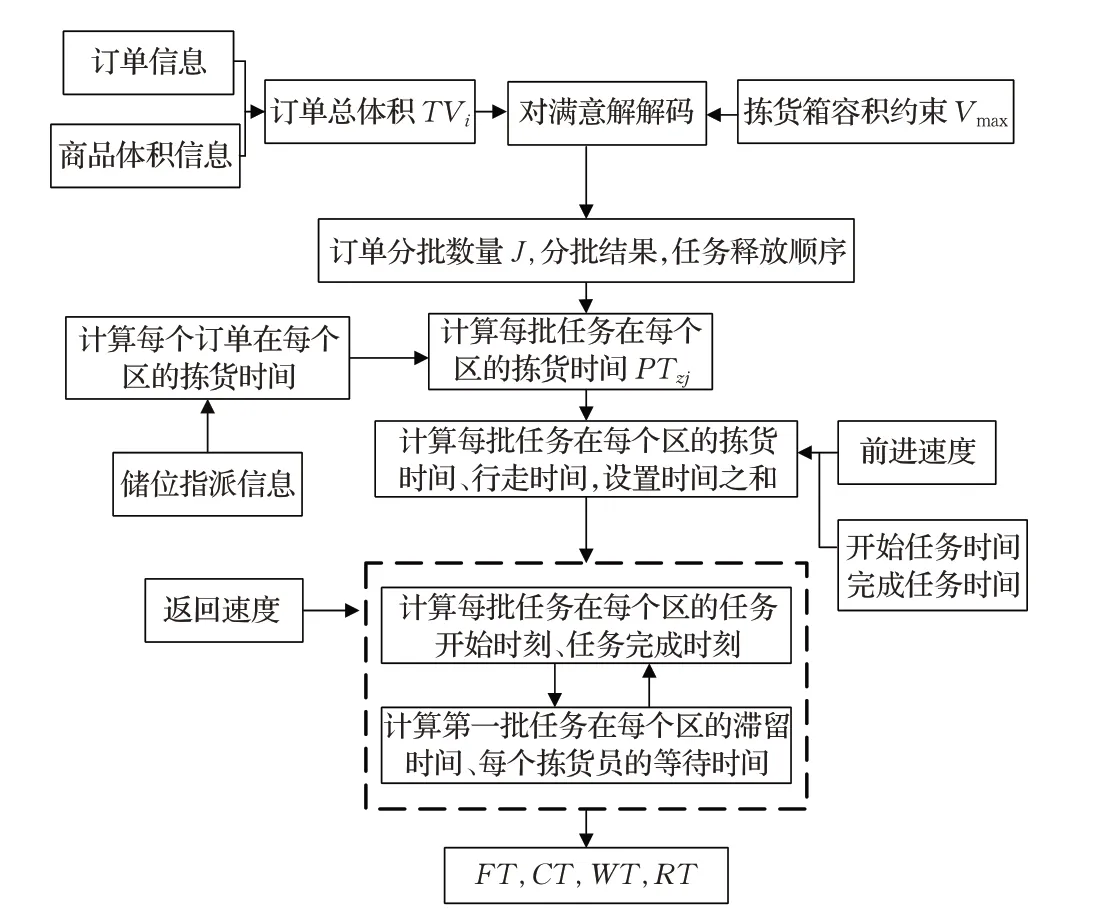
图10 满意解求各指标值的流程图

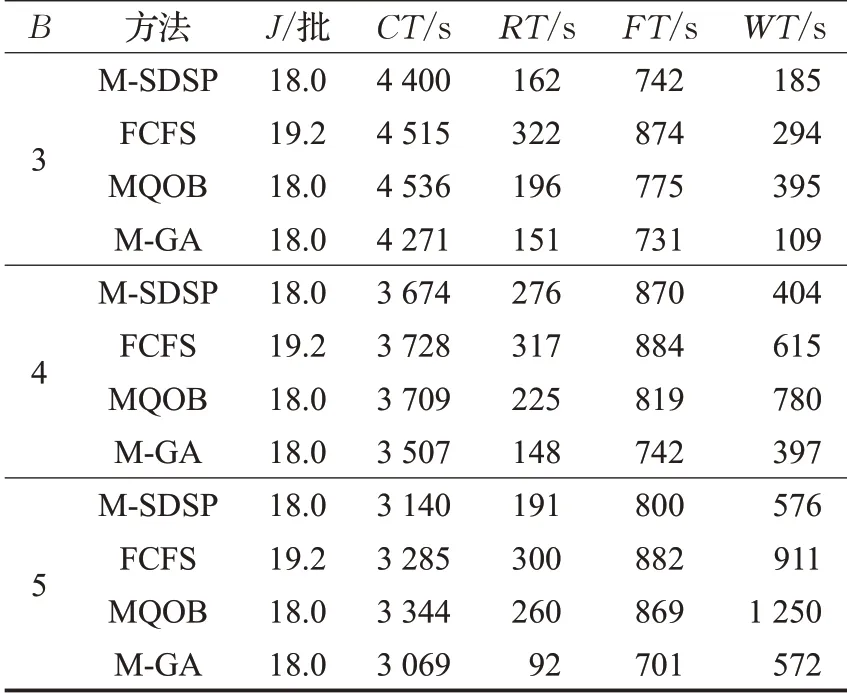
表1 1组订单的各指标值

表2 10组订单M-GA相对其他方法各指标的平均优化率%

从表1 可以看出，M-GA 在所有任务的完成时间CT ，在系统中的滞留时间RT ，平均履行周期FT 和拣货员在系统中的等待时间WT 等指标中，均不同程度小于M-SDSP、MQOB和FCFS的指标值。FCFS方法的订单分批数量均多于M-SDSP、MQOB和M-GA，这是由于FCFS方法中订单到达随机，在拣货箱容量约束下，订单分批次数不能完全达到最小批次数。

从表2可以看出，M-GA相对于M-SDSP、MQOB和FCFS 方法，在不同分区数量下，所有任务的完成时间CT 平均优化率达到2%～8%，在系统中的滞留时间RT的平均优化率达到34%～68%，平均履行周期FT 的平均优化率达到8%～19%，拣货员在系统中的等待时间WT 的平均优化率达到15%～75%。可以得出：本文提出的MSD 方法在各项指标中，均优于先到先服务订单分批方法和以最小化订单分批数量为目标的订单分批方法；并且设计的改进遗传算法M-GA优于基于节约原则的种子算法M-SDSP。

相比两种传统的订单分批模型，本文提出的考虑减小相邻区域时间差值的订单分批数学模型在达到最小分批数量的情况下，减小了相邻区域作业时间差值之和，进而缩短了拣货员的等待时间WT 和货物在系统中的滞留时间RT ，任务的平均履行周期FT 和所有任务的完成时间CT 也相应减少。

通过以上案例可以看出，在分区拣选系统中，相邻区域作业时间的差值不能完全等同于拣货员的等待时间WT 和货物在系统中的滞留时间RT ，但降低差值之和可以降低WT 和RT ，缩短任务完成时间CT ，进而提高拣货员的工作效率。

实验结果表明，拣货员人数的增加，加快了拣货作业进程，减少了所有任务的完成时间，进而提升了系统效率；但人力成本也会增加，区域之间作业时间的差异也会增加拣货人员作业的不平衡性，造成更多货物滞留与人员等待上的时间浪费。管理者需要在增加系统效率的收益与控制人员成本、降低时间消耗的付出之间权衡，结合各方面因素，找到一个合适的分区数量进行空间布局。

6 储位指派策略优化

货架高低会影响拣货员拣取货物的便捷性。货架不同层存储的货物拣取时间不同，从资料中得出，第三层货物最容易拣取，因此考虑拣选频率较高的商品存储在第三层，拣选频率较低的货品存储在底层或第四层，每层内部随机存储，增强存储的灵活性，如图11 所示，从上往下分别存储C 类、B 类、A 类、C 类。根据其特点称其为分类随机存储，其正视示意图如图12所示。

图11 流利式货架分类随机存储侧视示意图

图12 分类随机存储侧视示意图

在前一章中采用了随机存储的指派方式，随机存储是流利式货架中较为常见的存储方式，本文旨在随机存储上进行优化。设计实验比较随机存储和分类随机存储两种储位指派方式在各指标上的表现。在两种储位指派方式下，用本文提出的考虑相邻区域拣选时间差值的MSD 订单分批方法计算前文生成的10 组订单数据在3区、4区、5区情况下的各指标值。

为了更清楚看到储位指派的效果，增加两项指标，第一是任务平均理想履行时间DT ，即任务在系统中无滞留的时间，是每个区域拣货员的任务开始时间、拣选时间、人员的前进行走时间和任务完成时间之和，可以衡量人员在系统中的有效工作时间，分析储位指派方式在拣货时间上的优化效果；第二是拣货员工作时间的标准差SD，通过计算每个拣货员在其负责区域的工作时间（不包含等待时间），得到拣货员工作时间的标准差，以衡量拣货员的工作负荷平衡。

表3展示了1组订单在不同储位指派方式下用M-GA求得的各项指标值，计算分类随机存储相对于随机存储各指标的优化率，计算10 组实验各指标优化率的平均值得到表4。

表3 1组订单在不同指派方式下的各指标值

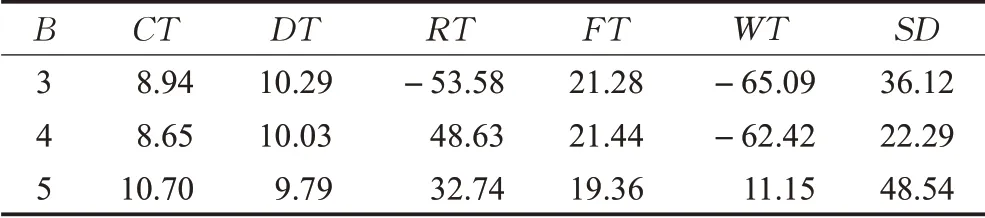
表4 分类随机存储相对于随机存储各指标的平均优化率%

从表3 中可以看出，第一组订单在不同分区数量下，分类随机存储在所有任务的完成时间CT 、理想履行时间DT 、平均履行周期FT 和拣货员工作时间的标准差SD 均优于随机存储。从表4 可以看出，分类随机存储相对于随机存储，所有任务的完成时间CT 优化了8%～10%，理想履行时间DT 优化了10%左右，所有任务的平均履行周期FT 优化了20%左右，拣货员工作时间的标准差SD 优化了22%～49%。由于任务平均理想履行时间DT 的缩短并不能缩短相邻区域作业时间的差值，故拣货员的等待时间WT 和货物的滞留时间RT不一定被优化，但因为其缩短了所有任务的拣选的时间，因而提高了整体的运行效率，使得分类随机存储整体表现优于随机存储。

储位指派方式会影响每个区域的拣货时间，进而影响相邻区域的作业时间差异。分类随机指派方式考虑将拣选频率较高的商品存放至拣货员最易拣取的层数，从根本上减少了每个区域的拣货时间，提升了系统效率，这种思想会在订单规模较大的情况下表现得更明显，从而对整个仓库的运行产生比较重要的影响。

7 结束语

流利式货架作为拣选周转频率较高货品的常用货架，其拣选效率的提高具有很重要的实际意义。本文考虑流利式货架拣选系统的特点，提出以最小化相邻区域作业时间差值之和与最小化订单分批数量为目标的订单分批模型，相比传统的先到先服务订单分批和以最小化订单分批数量为目标的单目标订单分批方法，在所有任务的完成时间、总滞留时间、平均履行周期和所有拣货员的等待时间指标上，均表现优秀。将本文的改进遗传算法与基于节约原则的种子算法对比，验证了本文算法的求解效果。分区拣选系统需要考虑相邻拣货员之间的影响，所以本文提出的订单分批模型不仅要考虑分批结果，还要考虑任务释放顺序。在遗传算法设计中，也考虑了这一点。

储位指派优化中，提出的分类随机指派方式充分考虑了拣货员操作的便捷性，从拣货人员的角度出发，在不增加拣货员作业节奏的同时，整体缩减拣货时间。这种将拣选频率较高的货品存放至拣货主体最容易拣取层数的这种思想也可以应用到更多拣选场景中。

在拣选系统中，本文的拣选主体是拣货员，随着机器人技术的普及，本文的研究成果也可以应用到机器人拣选中。

本文研究的流利式货架分区拣选系统中，拣货员不可跨出自己的区域帮助其他拣货员进行拣选，未来可以对工作人员跨区协同拣货进行深入研究。