不平衡样本下的金融市场极端风险预警研究

温廷新，孔祥博

辽宁工程技术大学 系统工程研究所，辽宁 葫芦岛125105

1 引言

近年来，经济全球化发展和互联网金融的普及使中国正置身于高速驶进的金融列车之上，中国金融市场走向有越来越强的趋势。金融理财产品更加多样化，诸多产品的创新为传统金融市场开启了新大门，市场结构也在不断发生着改变。短期融资券的发行、债券市场结构变化和股票市场融资功能使得直接融资规模得以提高。市场交易者结构、管制措施、定价机制、交易品种类等也都发生了变化，给金融市场带来潜移默化影响的同时也带来更多的风险。从整体上来讲，我国金融市场较其他发达国家而言成立时间尚短且存在许多隐患问题，经历数次金融市场的动荡起伏考验更加暴露出了其体系不完善及抗风险性弱等问题。

金融市场风险是金融市场变量变动或波动引起的金融资产未来价值的不确定性。而极端金融风险（extremely financial risk）会给生产生活带来严重损失，将导致金融市场的剧烈动荡并引起资产的暴涨暴跌。金融风险广泛蕴含于各种金融交易和商品交换的信用支付过程中，属于系统性风险，并且其易成为其他类型金融风险的引发因素。金融风险的类型主要涵盖价格风险、汇率风险、利率风险和通胀风险。

为了应对金融风险灾害，众多学者提出了不同算法并构建预警模型来预测金融市场极端风险的发生。Ahn 等运用SVM 对金融市场风险进行建模，结果表明其能够有效预测金融市场风险[1]。林宇、黄迅等人起初运用随机欠采样（RU）和少数类过采样（SMOTE）算法结合支持向量机对金融市场极端风险进行预测[2]，后通过改进利用自适应合成抽样法和逐级优化递减欠采样方法对SVM进行了改进，使得模型能够克服SMOTE的过拟合问题[3]。肖斌卿、杨旸等人利用遗传算法（GA）优化人工神经网络（ANN）模型对2013年我国金融安全状况进行了预测[4]。李梦雨用K-means 算法对金融系统风险进行分类，然后利用BP 神经网络建立金融系统风险预警模型[5]。衣柏衡、朱建军等人对SMOTE 算法进行了改进，并将其应用于小额贷款公司客户信用风险评估[6]。蒋先玲、张庆波将SMOTE 算法和随机森林结合的模型应用于供应链金融信用风险中并建立信用风险评估指标体系以获得更准确的结论[7]。徐国祥和杨振建利用主成分分析和遗传算法结合支持向量机模型[8]构建了PCA-GA-SVM 模型，分析了影响沪深300 指数的特征指标，并对金融风险进行了预测。以上学者对于金融风险模型的构建及论证已经有了一定的成果，为我国金融风险预测做出了贡献，但模型求解效率与准确度仍有改进余地。

极端金融风险出现的事件概率较小，因此数据样本存在明显的样本不均衡情况，此情况将导致模型训练时易出现过拟合问题。SMOTE方法是众多学者公认的平衡样本的方法，而支持向量机也是一种高维度区分能力显著且泛化能力较强的算法。在本文中SMOTE用于对不平衡数据样本进行过采样，然后使用因子分析来提取特征，后通过粒子群优化算法全局搜索支持向量机的最优参数，利用最小二乘支持向量机LSSVM 降低计算复杂度并提升效率，构造了SMOTE-PSO-LSSVM的风险识别预测模型，提高了识别金融风险能力和风险预控水平。

2 相关理论

2.1 粒子群算法

粒子群优化（Particle Swarm Optimization，PSO）是Eberhart 和Kennedy 在1995 年提出的一种全局搜索算法，结合了动物仿生中鸟类觅食和群聚的行为。它将每个优化问题视为搜索空间中的鸟或粒子，并且每个粒子具有由适应度函数所调整的值。每个粒子还具有飞行速度和方向特征，之后粒子会在迭代寻优中被优化。

在每个迭代寻优过程中，粒子通过个体极值和种群极值进行自我更新：粒子本身所发现的最优解（个体极值pbest）和当前由整个种群发现的最优解（全局极值gbest），即：

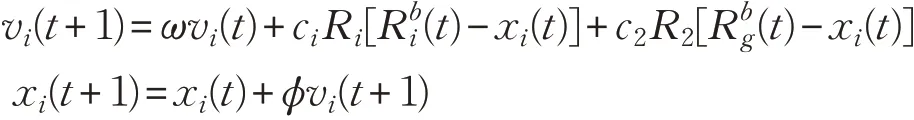
式中，t 是迭代次数；vi(t)是第i 个粒子在t 次迭代的速度；ω 是惯性权重参数；c1,c2是认知系数；R1,R2是均匀分布随机数；Rbi(t)是粒子i 个体历史最优位置；Rbg(t)是群体历史最优位置；xi(t)是粒子在t 次迭代的位置；φ 是一个收缩因子，用来保持速度在一定范围内。

PSO算法是一种随机搜索和并行优化算法，其优势在于简单、鲁棒性好、易于实现、速度快，易找到问题的全局最优解，故本文选择PSO算法对最小二乘支持向量机进行寻优来建立金融风险预测模型。

2.2 最小二乘支持向量机

Suykens等人[9]修改了SVM进而得到了最小二乘支持向量机，它以最小平方误差作为损失函数，并使约束中的不等式约束化为等式约束。

对于给定的数据集(xi,yi),x ∈Rl,y ∈R,i=1,2,…,n,其中，xi是输入数据，维度是l ；yi为对应的输出数据。针对LSSVM，求解最优化问题的目标函数：

式中，φ(⋅)是非线性函数，w 是权值，b 是偏置项，ei是误差，C 是惩罚系数。

通过拉格朗日乘子将式（1）中的约束优化问题变为无约束优化问题，对应的拉格朗日函数表达式为：

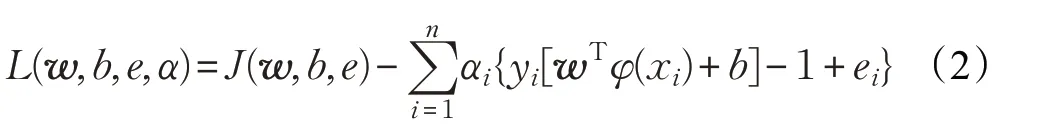
式中，αi是拉格朗日乘子。

对式（2）中的变量求偏导，采用径向基核函数（Radial Basis Function，RBF）：的分类函数表达式如下：

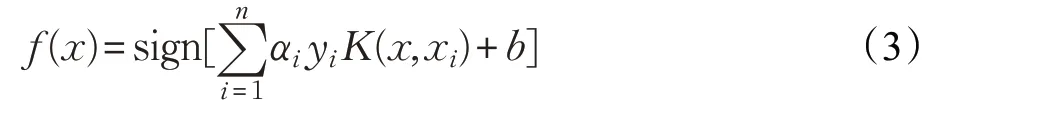
惩罚参数C 和核参数σ 对LSSVM 模型的训练学习能力以及泛化能力起到决定性作用，LSSVM 的分类效果也是由C 和参数σ 的值共同决定的。

3 极端风险预警模型构建

3.1 极端风险样本界定

极端金融风险的主流鉴定方法目前有两种，其一是以金融危机发生时间段作为危机样本划分依据来划分危机样本，其二是使用EVT 值作为门槛约束来过滤出危机样本，如果样本值低于门槛值则界定为危机样本，反之若高于门槛值则为非危机样本。以上两种方法都有其各自优势，目前没有最优的标准。本文将通过把金融危机时期和EVT 两种界定方法结合的方式确定指标，共同界定极端风险样本。将既发生在危机时间段内又低于EVT 门槛值的样本界定为极端风险样本，其余样本认定为非极端样本。

表1 CSI 300与其余收益率之间的下尾相依系数

表2 不同方法求解门槛值

常见的EVT门槛值确定方法有：Hill图法[10]、MEF图法[11]、峰度法、1.65σ 估计法[12]、10%估计法[13]。本文将计算上述5种求门槛值的方法，并最终求平均值μˉ作为界定值。

3.2 特征指标变量选择与提取

特征指标变量的选择直接影响模型构建的好坏和预测性能，因此对于指标变量的选取已经有学者提出适合的指标[2]。所提出的8项股指基本指标内部特征指标分别为开盘价、收盘价、最高价、最低价、成交量、成交额、涨跌额、涨跌幅。本文另外加入两项特征指标前收盘价和换手率。收益率能更好地反映市场综合信息，从而选取8 个外部风险特征指标收益率来反映国际金融市场对国内金融市场的影响，外部风险特征指标为：恒生指数日收益率（HSI）、韩国股指日收益率（KOSPI）、台湾加权指数日收益率（TWII）、标准普尔指数日收益率（GSPC）、纳斯达克指数日收益率（NASDAQ）、日经225指数日收益率（Nikkei225）、道琼斯工业平均指数日收益率（DJIA）、英国金融时报指数（FTSE100）。

利用下尾相关系数检验两个市场同步的概率，刻画国外股指对中国股指的影响程度[14]。由Clayton Copula计算的沪深300与国外股票指数下尾相依系数如表1所示。

观察表中数据发现下尾相依系数大于0.1的有HSI、KOSPI 和TWII，小于0.1 的有Nikkei225 和FTSE100，趋近于0 的有GSPC、NASDAQ 和DJIA。因此本文选取HSI、KOSPI和TWII作为外部特征指标，参考文献[2]中已经对指标进行卡方检验并通过拟合优度检验证实了其有效性，这里不再论证。

模型训练样本数据为2014年12月10日—2015年9月10日沪深300指数共计185条样本，查阅相关资料得出极端危机发生时间段为2015 年6 月15 日—2015 年9月10日共计61条数据。

利用上述的五种计算门槛值的方法确定各自门槛值并求平均，结果如表2所示。

根据门槛值均值进行样本筛选，将发生在极端危机时间段内且低于门槛值的样本归为金融极端风险样本，共计26条。

3.3 SMOTE-PSO-LSSVM模型构建

观察样本数据发现极端风险样本与正常样本在数据量上有较大差异属于不平衡样本集，因此需要利用过采样算法将少数类样本进行扩充合成新样本。

SMOTE 算法过程：少数类样本集设为T ，则最终少数样本将被合成NT 个新样本。声明N 必须是正整数，当给定N 为小于1的数时算法将N 视为1。

过程如下，取一个少数类样本i，它的特征向量xi,i ∈{1,2,…,T}：

（1）找到少数类样本xi的k 个近邻样本，利用欧氏距离计算得出，记作xi(near),near ∈{1,2,…,k}。

（2）从这k 个近邻样本中随机选择一个样本xi(nn)，通过生成一个0至1之间的随机数ς1，合成新样本xi1：。

（3）重复步骤（2）执行N 次，得到N 个新样本：xinew,new ∈1,2,…,N 。对全部T 个样本进行如上操作得到NT 个新样本。

通过上述方法共合成风险样本总计130条，使风险样本与正常样本数据量基本平衡。在模型运算之前需要对数据进行归一化操作消除量纲影响。

使用因子分析法对归一化后的数据进行因子分析提取主要影响因子[15]，将X1收盘价、X2最高价、X3最低价、X4开盘价、X5前收盘价、X6涨跌额、X7成交量、X8成交金额、X9 涨跌幅、X10 换手率利用SPSS 软件首先进行KMO 样本测度及巴特莱特（Bartlett）检验，得到结果如表3。由表3可得，KMO值为0.811，说明这10个变量适合作因子分析，且Bartlett 球体检验统计值显著性概率Sig.值为0小于0.05，因此再次说明了这10个相关性较强的变量适合作因子分析。

表3 KMO样本检验与巴特莱特球体检验

使用SPSS 对这10 个变量进行因子分析得到方差解释如表4，从表4 中看出这10 个特征中可以提取2 个公共因子F1和F2，特征值均大于1，总贡献率为89.791%，即这两个因子包含了原始10个指标中89.791%的信息量，碎石图（见图1）同样显示拐点接近于第二个特征值位置。

表4 总方差解释

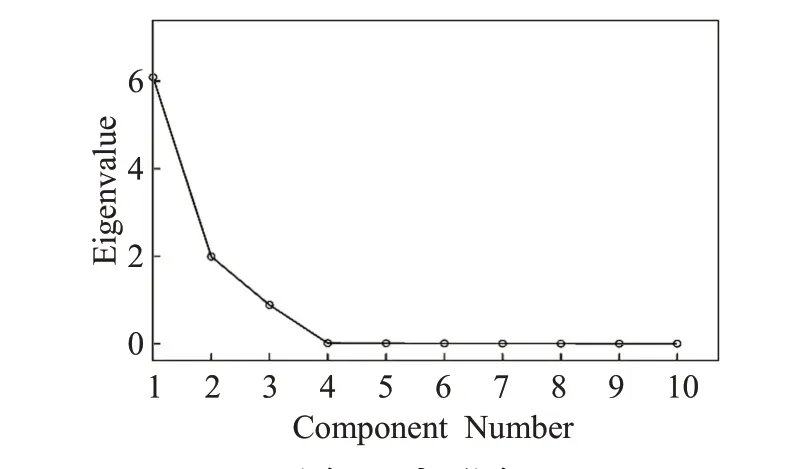
图1 碎石图

利用SPSS 得到两个因子F1和F2与原始10 个特征的因子载荷矩阵，如表5所示。从表5中可以发现，所提取的两个因子中F1由收盘价、最高价、最低价、开盘价、前收盘、成交量、成交金额构成，而F2由涨跌额、涨跌幅及换手率构成，F1及F2部分取值见表6。

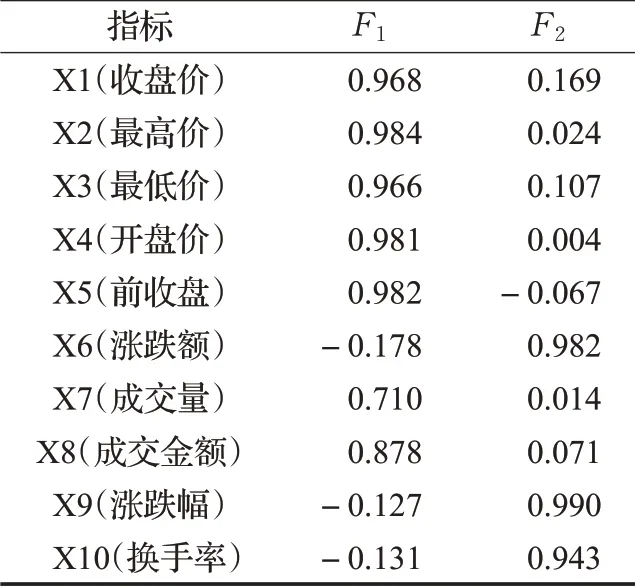
表5 因子载荷矩阵

表6 F1 与F2 取值

将提取的主成分F1、F2作为PSO-LSSVM 的输入向量，将分类结果（极端风险样本、正常样本）作为输出向量建立模型。通过使用Matlab2014a 进行编程，设置粒子群种群规模为30，进化300次，得到图2所示适应度变化曲线，从曲线可以看出迭代70 次时适应度趋于平缓不再发生改变，此时得到LSSVM的最优参数。

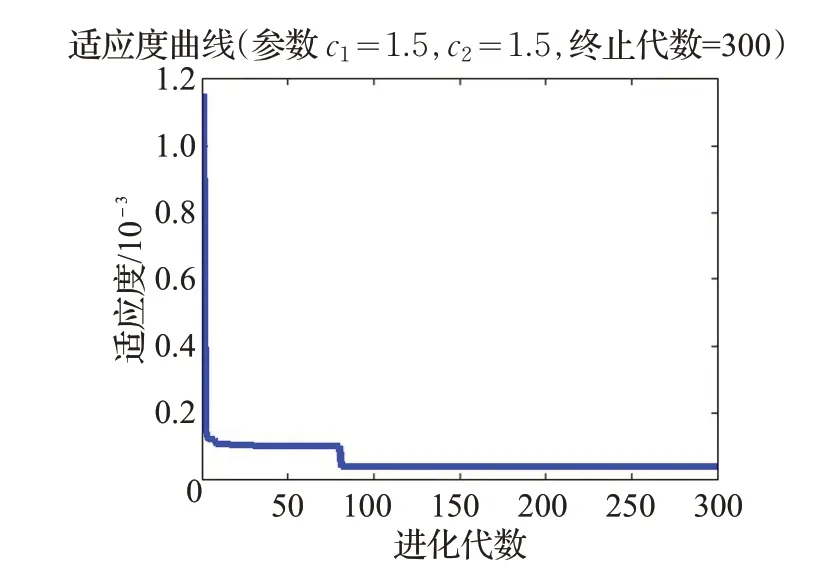
图2 适应度变化曲线

3.4 SMOTE-PSO-LSSVM模型性能对比评估

为了对比SMOTE-PSO-LSSVM与其他模型在精度和效率方面的性能优劣，选择了LSSVM、GA-SVM、PSO-SVM、BPNN、PSO-LSSVM进行对比实验。

实验测试数据选取了我国2007 年—2010 年沪深300指数并进行了数据预处理，样本中含极端风险样本193条，将遗传算法的迭代次数设置为300，种群大小设置为40，交叉概率设置为0.8，变异概率为0.1，经过反复试算确定SVM 模型参数为：krnel_type=“RBF_kernel”，cost=1，eps=0.0020，degree=4；粒子群算将迭代次数设置为300，种群大小也是30，最大粒子速度设置为0.01，最小值为-0.01，粒子大小介于0和1之间，加速常数设置为2，最大权重系数ωmax=0.9，最小权重系数ωmin=0.1。BP 神经网络将输入层设置为2 个节点，隐藏层节点数为9，输出层节点为2（1 表示为[10]，2 表示为[01]，选择其中120个样本进行训练，用30个样本进行测试，采用5折交叉验证共实验30次，并将最终结果取平均值，对比结果如表7所示。

表7 不同模型预测结果比较

从表7 中可以得出SMOTE-PSO-LSSVM 算法在预测金融风险样本上的效果提升明显，准确率高于其他模型，在运行速度上相较于遗传算法和粒子群优化的支持向量机也有了明显的提升，原因是采用最小二乘支持向量机降低了运算复杂度提高了效率。

将不同模型作用在沪深300 指数数据上并预测20条样本测试数据（分类1为风险样本，2为正常样本），预测结果如图3 所示。从图3 中可以看出SMOTE-PSOLSSVM 模型预测精度很高仅错判了一个样本，误判率低于其余四种模型，其作用在不平衡数据样本集上效果尤为明显。

图3 各模型效果对比

4 结论

本文利用沪深300 数据对中国金融市场极端风险进行预警研究，通过用SMOTE、PSO与最小二乘支持向量机LSSVM 组合以构建SMOTE-PSO-LSSVM 模型。与LSSVM、GA-SVM、PSO-SVM、BPNN、PSO-LSSVM对比发现SMOTE-PSO-LSSVM模型具有优秀的金融风险识别能力，在精度与准确率上均优于其他模型。

通过研究证实了SMOTE-PSO-LSSVM模型能够较为准确预测我国金融市场极端风险的发生，对金融市场的风险把控起到了一定的作用。同时可以使投资者更加警惕危机的来临，对投资决策金融理财产品以及把握买卖时机等起到了关键作用。