面向医疗辅助诊断的可视化多属性决策方法

陈 杰，程 胜，徐 梦，史豪斌

1.中国载人航天办公室，北京100083

2.中国航天科技集团公司 软件研发中心，北京100094

3.西北工业大学 计算机学院，西安710072

1 引言

当今社会，计算机已经成为了医学现代化的一种必不可少的工具，计算机辅助诊断已经渗入到了现代医学的方方面面。在传统的医疗诊断中，病因探寻、疾病诊断、合理治理等需要专家依据已有的经验进行决策，这无疑增加了专家们的主观疲劳，甚至可能因为疲惫出现误诊的情况，因此如何使用计算机辅助决策成为了一个热门的课题[1-3]。在医疗辅助诊断中，医疗病症分析以及病情诊断往往存在着多个病情属性。以阑尾炎诊断问题分析，通常阑尾炎疾病分为慢性阑尾炎、急性阑尾炎、阑尾炎穿孔三种不同的类型，症候指标有腹痛开始部位、恶心呕吐、大便、压痛、肌紧张和反跳痛、体温和白细胞数几种指标去评估阑尾炎疾病的种类，阑尾炎疾病的诊断明显属于一类多属性决策问题。

多属性决策是智能决策理论研究中的重要内容，已经被广泛应用于工业过程管理、战术武器评估、战场态势评估、经济效益评估、智能辅助医疗等领域中，对人们的生产生活产生了巨大的作用[4]。同时，作为多属性决策领域的重要分支，近年来，多属性群决策方法的研究热点集中在如何高效配置多属性决策方法的权重[5]、如何设计高效的不同群体交互方式[6]、决策属性与决策权重等作为先验条件不被完全所知情况下的群体决策一致性验证方法等方面[7]。数据聚集算子是数据聚集过程中的一个十分简单，但是十分有效的工具，是多属性决策方法中常用的方法之一[8]。

多属性决策方法充分考虑到决策属性权重系数与属性要素的配置对于决策水平的影响，基于多属性决策理论的辅助决策方法具有解决医学辅助诊断中多属性决策问题的可行性。但是目前多属性决策方法及其相关理论在医学辅助诊断上应用相对较少，本文结合多属性决策方法与复杂网络的相关理论，提出了一种面向医疗辅助诊断的可视化多属性决策方法。

文献[6]针对医学辅助诊断领域中的面向中风后吞咽功能障碍康复治疗的问题，首先给出了一种群体智慧定义以及群体智慧涌现方法，在此基础上，给出了一种基于群体智慧的多属性决策方法，使计算机能够学习群体经验并进行自动决策以实现医学辅助诊断。但是该方法面向群体智能决策，并未讨论个体多属性备选方案辅助决策的方法。文献[9]针对一类多属性群体决策问题进行了探讨，提出了一种广义直觉模糊OWA算子，但是该工作仍然存在一定的缺陷。例如，OWA 算子侧重于数据本身对权重的影响，并未考虑到数据之间的关联以及数据的位置对于权重的作用，因此具有一定的片面性。文献[10]探讨了一类多属性决策领域中决策矩阵元素为区间数的不确定的问题，提出一种基于幂均算子的区间型多属性决策方法。但是，该工作存在的问题是使用幂均算子计算数据之间的支持度，但是没有考虑到数据之间的重要性。在实际情况中，不同重要性的数据需要被赋予不同的权重。

本文针对医疗辅助诊断中的多属性决策问题进行研究，受启发于先前工作[8，11]，结合了复杂网络[12]的相关基础理论，提出了一种面向医疗辅助诊断的可视化有序加权几何平均算子，综合了有序序列中数据的位置、数据的重要程度、数据间的支持度等属性。本文主要有以下三个方面的贡献。首先，针对医学诊断问题，考虑到以往决策算子的弊端，给出了一种具有可视化性的有序加权几何平均算子，该算子通过可视图理论[13]将有序加权几何算子中的有序数据集合转化为复杂网络中的结点集合，复杂网络中的结点与有序数据一一对应，复杂网络中结点之间的连接关系反应了数据之间的可视性。其次，借鉴库伦定律[14]，设置了一种支持度函数，支持度函数反应了网络中某个结点受其他结点的支持程度，该支持函数不仅考虑到了结点之间的距离也考虑了结点自身数值的大小。最后，基于可视化有序加权几何平均算子与支持度函数设计了一种可视化多属性决策方法，该方法被用于解决医疗辅助诊断中的多属性决策问题。

2 多属性决策算子

2.1 有序加权几何算子

在军事、管理以及生产的各个领域中，数据信息的融合技术起着至关重要的作用，同时人们对信息融合算子也一直给予高度的重视。著名学者Saaty等人在1983年提出了著名的加权几何平均算子（Weighted Geometric Averaging，WGA）算子[15]。加权几何平均算子是一种简单易用的信息融合算子，该算子是对每个数据进行加权，加权的依据是每个数据的重要性，然后进行融合。随后在1988 年，Yager 等人提出了一种有序的加权几何平均算子（Ordered Weighted Geometric Averaging，OWGA）[16]。有序算子与经典算子的区别在于前者是对给定的数据信息从大到小进行有序排序处理，并通过对数据信息所在的位置进行加权后融合。但是，后者并没有考虑到数据信息的融合过程可能和数据的位置有一定关系。

定义1 设定一组原始的数据(a1,a2,…,an)，首先对该组数据进行从大到小的排序，获得有序的数据(b1,b2,…,bn)，定义有序加权几何平均算子为：

式中，ω=(ω1,ω2,…,ωn)T是指数加权向量，其中，ωi∈。本文定义bi是一组数据(a1,a2,…,an)中第i 个数值最大的数据。在有序加权几何平均算子中，原始的数据ai与权重无关，而权重与数据融合过程中的位置有关。但是在该算子的设计中，权重的设计没有考虑到数据本身的大小以及数据之间的相互支持度。

2.2 最大熵OWA算子

OWA算子具有两种测度，分别是orness测度与andness测度[17]。针对OWA算子中权值难以确定的问题，文献[18]基于orness测度水平，结合OWA算子与最大熵原理，给出了基于最大熵原理的OWA算子求解的非线性规划模型，如公式（2）所示：

其中，Disper(W)表示权重向量W 的离散度，orness(W)表示具有权值向量W 的OWA算子的orness测度。

使用Lagrange算法求解OWA算子的多项式得到该模型的解析解[19]。

如果α=0，则W=[0,0,…,1]T；如果α=1，则W=[1,0,…,0]T。

如果n=2，则w1=α,w2=1-α。

若n ≥3,0 ＜α ＜1，则：

3 用于医学辅助诊断的可视化有序加权几何算子

3.1 库伦定律

库伦定律是在1785年由法国科学家库伦由实验发现，该定律描述了真空中相距为d 的电荷Q1,Q2之间相互作用力的物理规律。其主要思想是，静止不动的两个点电荷之间相互作用力的计算需要考虑它们的电荷量的乘积以及它们之间距离，而力作用于它们之间的直接连线。库伦定律的表示形式如下所示：

其中，k 为常数，F(Q1,Q2)表示静止电荷Q1,Q2之间的相互作用力，d 是两个静止电荷之间的距离。该定律描述了一种空间中的两个结点之间相互作用力的基本形式。近些年，库伦定律模型的思想已经开始应用到了复杂网络的相关研究中，并引起了学者的广泛关注[14]。

3.2 支持度函数

Lacasa等人在2008年提出了著名的可视图（Visibility Graph，VG）理论，可视图理论建立了时间序列与复杂网络之间的联系，该算法可以将时间序列简单快速地转变为复杂网络[20]。复杂网络中的结点与序列中的数值一一对应，结点之间的连接关系反应在了数据之间的可视性。可视图的定义如下所示。

定义2 设定使用二元组表示的两个数据(i,bi)与(j,bj)，如果两个数据之间具有可见性，则对于任意一个在二者之间的数值(k,bk)均满足：

在可视图中，如果两个数据之间满足可见性，则在可视图中两个结点会被连接。在复杂网络理论中，结点的度一定程度上反映了该结点的重要性，结点的度就是与结点相连的边的个数。一般而言，结点的度越多，结点受其他结点的支持程度越多，结点的支持度往往通过支持度函数来描述，但是如何定义结点的支持度函数一直是一个广受学者关注的问题。本文受到库伦定律的启发，结点的支持度的计算不仅需要考虑结点之间的距离同时考虑结点自身数值的大小。

定义3 设定复杂网络中存在结点Oi,Oj，两个结点的数值分别为Oi,Oj，两个结点之间的距离为dij，定义两个结点之间的支持度函数为：

其中，n 为任意一个正整数。 Sups(OiOj)表示结点Oj对结点Oi的支持度。网络中的所有结点对结点Oi的支持度之和定义为：

3.3 可视化有序加权几何平均算子

使用O={O1,O2,…,On}为一组从大到小的有序数据，该组有序的数据共计有n 个数据，可视化有序加权几何平均算子可以表示为：

K(Oi)表示网络中其他结点对结点Oi的支持度之和，其中。能够对结点Oi产生支持度的结点与之均满足可见性。

本文提出的可视化有序加权几何平均算子借鉴了库伦定律的基本思想。该算子的实际意义是相对于有序加权几何平均算子，该算子将序列中的数据映射为复杂网络中的节点，这使得在计算序列的评估值的时候不仅能够考虑到数据所在的位置对于结点权重的影响，也考虑了结点之间的距离与结点自身数值的大小对于决策结果的影响。理论意义在于，通过一种可视化理论建立了有序加权几何平均算子与复杂网络之间的联系，并借用库伦定律计算结点之间的支持度，这为面向医学诊断的决策算子的权值估计提供一种新的方法。

3.4 案例分析

设定存在一组数据，该组数据的数值分别为：55，45，50，40，70，75，80，85，60。现使用本文提出的可视化多属性决策方法对这些数据进行评价。具体过程如下：

步骤1 首先将这组数据有序化，得到85，80，75，70，60，55，50，45，40。

步骤2 根据可视图理论计算出每一个结点的可见性结点，计算得到：结点85 的可视化结点为80；结点80的可视化结点为：85，75；结点75 的可视化结点为：85，80，70；结点70 的可视化结点为：85，80，75，60，55，50，45，40；结点60的可视化结点为：85，80，75，70，55；结点55 的可视化结点为：85，80，75，70，60，50；结点50 的可视化结点为：85，80，75，70，60，55，45；结点45的可视化结点为：85，80，75，70，60，55，50，40；结点40 的可视化结点为85，80，75，70，60，55，50，45。将该序列部分结点之间的可视化关系使用网络表示如图1所示。图1展示了序列中数值85，80，75，70 的连接关系，其中，结点0，1，2，…，8分别表示数值85，80，75，70，60，55，50，45，40。

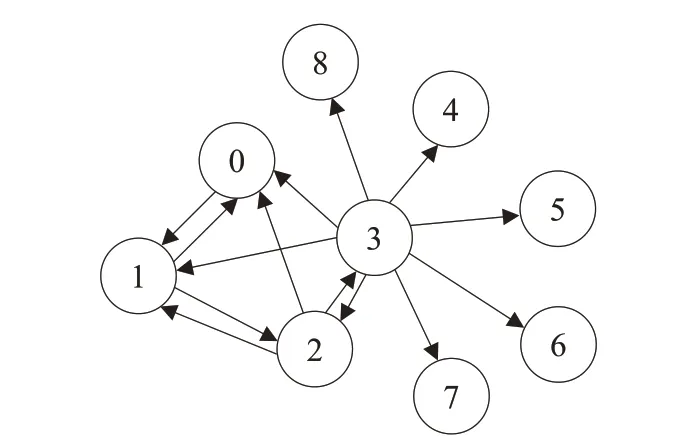
图1 部分结点的可视化网络图

步骤3 根据各个结点之间的连接关系用支持度函数计算出每个结点的支持度，与公式（6）中的库伦定律类似，本文设定n=2，以数值75为例，计算得到数值75的支持度为：

依次计算每个结点的支持度。

步骤4 基于每个结点的支持根据公式（11）计算得到权重向量为：

步骤5 根据公式（10）计算得到可视化有序加权几何平均算子为：

4 应用研究

4.1 可视化多属性决策方法在病情诊断中的应用

以某医院的1 002 例阑尾炎病例数据为例[21]，阑尾炎病例以其病理为标准诊断为慢性阑尾炎、急性阑尾炎、阑尾穿孔三种类型。现以医院的一个实际病例为例[22]，病情从上腹开始疼痛、伴以强烈的恶心与呕吐、腹泻、大于右下腹压痛、肌紧张与反跳痛强烈、入院体温39 ℃，脉搏120 次/s，白细胞数19.35×109/L。基于可视化多属性决策方法为医生提供治疗方案。定义频率为症候的指标例数/该疾病的总例数×100%。例如急性阑尾炎总计有494例，上腹开始疼痛有143例，则其频率为：143/494×100%=29%。阑尾炎病例统计表见文献[22]。

对于该实际病例，将各症候指标属性取对应的频率值，得到如表1的频率矩阵。

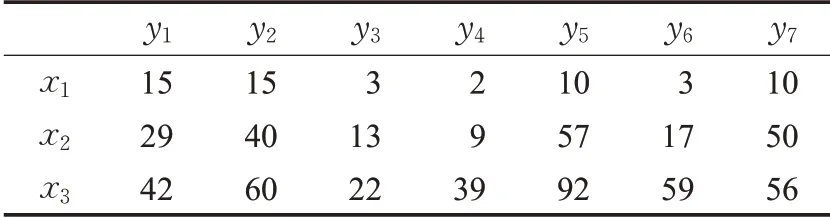
表1 频率矩阵

表1 中，方案集合X={x1,x2,x3},x1表示慢性阑尾炎，x2表示急性阑尾炎，x3表示阑尾穿孔，属性集合Y= {y1,y2,…,y7}分别表示腹痛开始部位等症候指标。基于可视化多属性决策方法对方案集合中的病例进行分析，同时用最大熵OWA 算子进行对比分析，最大熵OWA 算子的参数α 分别取为0.2，0.5，0.6，通过实验结果分析可视化有序加权几何平均算子（VOWGA）与最大熵OWA算子两种不同方法在该案例中所表现出的效果。分别使用VOWGA算子与最大熵OWA算子两种不同方法计算得到的三种方案的评估数值曲线如图2 所示。图2中横坐标分别表示三种不同的疾病，纵坐标分别表示计算得到的评估值。

图2 两种方法的方案评估值

从图2 的实验结果可以看出，本文提出的VOWGA算子计算得到的评估值与三种不同参数的最大熵OWA算子计算得到的结果，曲线趋势上是一致的。不同α 取值的最大熵OWA 算子包含主观因素的程度不同，而当α=0.5 时，包含主观因素最少，VOWGA 算子与包含不同主观因素最大熵OWA 算子计算得到的结果是相似的，这也说明了这两种方法对方案的评估结果是一致的，验证了本文提出方法的合理性。对于慢性阑尾炎x1，计算其可视化有序加权几何平均算子，得到VOWGAx1(y1,y2,…,yn)=11.178 1，依次计算得到急性阑尾炎x2与阑尾穿孔x3的可视化有序加权几何平均算子分别为：

明显x3＞x2＞x1，由此可以判断该病人是阑尾穿孔，而经过手术也确实证实了该病人是阑尾穿孔，由此可以看出本文提出的方法是有效的。

4.2 可视化多属性决策方法在病因诊断中的应用

病因诊断同样是医学辅助诊断中的一个重要的应用。基于所提出的多属性决策方法，本文以广西医科大学老年保健中心收集的2000年1月到2006年12月之间的7 085例60岁以上老年住院者的案例[21]来分析患者医院感染的原因，医院感染的影响因素包括：年龄段、疾病类别、是否使用广谱抗生素等。医院感染统计表见参考文献[23]。设定比例的计算方法：例数/总人数×100%。

本文将影响老年患者医院感染的影响因素分为年龄段、疾病类别、使用广谱抗生素与泌尿道插管等，未使用广谱抗生素与泌尿道插管等四种。设定方案集合X={x1,x2,…,xn}，属性集合Y={y1,y2}。对于年龄段，方案x1表示60～69 岁，方案x2表示70～79 岁，方案x3表示大于80 岁，属性y1表示老年住院患者，属性y2表示感染患者。对于疾病类别，方案x1表示呼吸系统疾病，方案x2表示消化系统疾病，依次类推，属性表示含义不变。对于使用广谱抗生素与泌尿道插管等，方案x1表示使用广谱抗生素，方案x2表示使用泌尿道插管，方案x3表示使用动静脉插管，方案x4使用呼吸机，属性含义同上。对于未使用广谱抗生素与泌尿道插管等，方案x1表示未使用广谱抗生素，方案x2表示未使用泌尿道插管，方案x3表示未使用动静脉插管，方案x4未使用呼吸机，属性含义同上。四种病因的频率矩阵如表2～表5所示。

表2 年龄段频率矩阵

表3 疾病类别频率矩阵

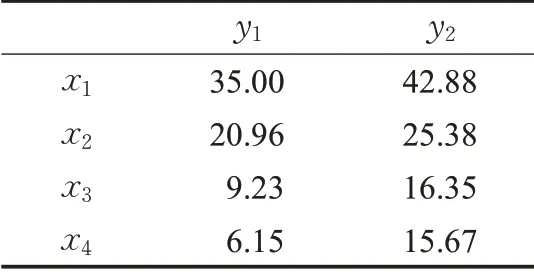
表4 使用广谱抗生素与泌尿道插管等频率矩阵

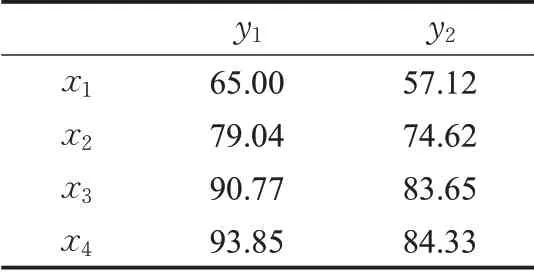
表5 未使用广谱抗生素与泌尿道插管等

同时使用可视化有序加权几何平均算子（VOWGA）与最大熵OWA 算子对该案例进行分析，设定最大熵OWA算子的参数α 取值分别为0.5，0.2，0.6。分别针对年龄段、疾病类别、使用广谱抗生素与泌尿道插管等，未使用广谱抗生素与泌尿道插管等四种不同的影响因素进行分析，计算得到的结果如图3 所示。与图2 表示含义类似，图3 中横坐标分别表示四种不同的决策方案，纵坐标表示计算得到的评估值。

从图3所示的实验结果可以看出，使用有序加权几何平均算子（VOWGA）与参数不同的最大熵OWA算子分别针对这四种因素的分析结果曲线一致，验证了本文提出方法的合理性。不同的算子计算得到的评估值是不同的，这是因为不同算子计算得到的权值不同，最大熵考虑数值本身大小对于权重的影响，但是这种方法没有考虑到数据的位置以及数据之间的关系对于权重的影响，VOWGA算子综合了数据的数值大小以及数值的位置对于权重的影响，在设置支持度函数的时候不仅考虑到了结点之间的距离对于结点的影响，同时考虑了结点的数值大小的影响。从图3 的实验分析得到，70～79岁之间的老人最容易医院感染，消化系统疾病是造成老人医院感染最主要的疾病因素，在所有医院感染的老人中，使用广谱抗生素导致感染的老人数量最多，因此，使用广谱抗生素是老人医院感染最主要的原因，图3（d）所展示的实验结果也验证了这一结论。观察表3 所得到的数据，其中，使用过呼吸机的老人患病几率为19.25%（82/426×100%），使用过动静脉插管的老人患病几率为13.00（85/654×100%），几率较高，因此，使用呼吸机与动静脉插管最容易导致老人医院感染。由此，医院在对住院老人治疗的过程中，应该慎用呼吸机与动静脉插管，少用广谱抗生素。

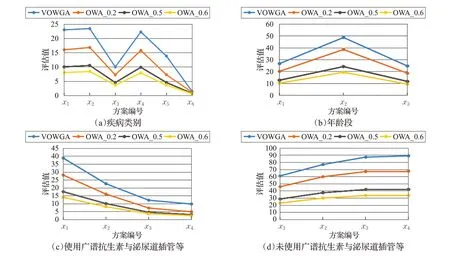
图3 疾病影响因素分析

5 结论

面向医疗辅助诊断问题，为了更加精准地分析医学诊断结果以为医护人员提供有效的决策支持，本文提出了一种可视化多属性决策方法。首先，使用有序加权几何算子将原始数据进行有序化处理，其次，提出了一种可视化有序加权几何算子，使用可视图理论建立有序序列中的数值与复杂网络中结点之间的关系，通过复杂网络中结点之间的连接关系展示了原始数据之间的潜在联系，最后，借用库伦定律设计了一种支持度函数，支持度函数描述了结点之间的支持度。本文提出的方法不仅考虑到数据自身数值的大小同时考虑到了数据的位置以及数据之间的可视化关系。最后，本文通过分析病情诊断与病因诊断两个实际医学活动中的案例验证了本文提出的多属性决策方法的有效性。本文在多属性决策于医学辅助诊断方面的工作较为基础，旨在为医学辅助诊断提供一种可视化多属性决策方法的新思路。