改进蚁群算法在AGV路径规划中的应用

胡春阳，姜 平，周根荣

南通大学 电气工程学院，江苏 南通226019

1 引言

路径规划是指在有障碍物的环境中，寻找一条从起点到终点的无碰撞最优路径[1]。传统的路径规划算法包括人工势场法[2]、启发式搜索法[3]、滚动窗口法[4]等。如今，随着智能算法的不断发展，越来越多的学者将遗传算法[5]、粒子群算法[6]、蚁群算法[7]等智能算法应用到路径规划上。

蚁群算法是Dorigo M 受蚂蚁觅食启发，于1996 年提出的一种仿生算法[8]。随着国内外学者大量研究，现已被广泛应用于解决旅行商问题[9]、车辆调度问题[10]、机器人路径规划问题[11]等。根据自然界中蚂蚁觅食时会在走过的路径上留下可被任意蚂蚁感知的信息素，单个蚂蚁觅食时便会选择信息素浓度较大的路径。随着蚁群不断搜索到食物并将其搬回至蚁穴，路径上的信息素浓度便越来越高，下一代蚂蚁便会通过此路径找到食物。由此可见，蚁群算法是一种正反馈算法，随着蚂蚁迭代次数的不断增多来逼近最优解。但这也使蚁群算法易陷入局部最优，且前期搜索目标盲目性较大，导致收敛速度慢[12]。为此，许多学者对蚁群算法进行改进。文献[13]对信息素进行优化，设定信息素最大最小阈值避免陷入局部最优，虽然有用但效果并不明显。由于蚁群算法参数对结果的影响明显，可传统算法却采用经验法设定参数，浪费大量时间[14]。因此，文献[15]中提出通过粒子群算法对传统蚁群算法进行参数优化，虽然效果明显，但执行时间过长。上述文献仅仅针对传统蚁群算法进行改进，主要解决旅行商问题。而对AGV 路径规划问题来说，大多研究采用栅格地图建立工作环境，并根据易陷入U 型陷阱的特点对传统蚁群算法改进[16]。文献[17]采用一种自适应参数的改进蚁群算法，使得算法在前期收敛速度较快，在后期局部搜索能力变强。但仍未解决算法易陷入局部最优的问题。文献[18]提出了一种基于头尾双向搜索的A*启发函数算法来改进传统蚁群算法，很大程度上提高了算法运行速度和全局搜索能力。但是，由于采用了头尾相遇即停止策略，对局部搜索能力提高不足。文献[19]对移动机器人的路径规划中采用多指标条件，根据AGV小车路径弯折度、运行到位时间、能耗问题等进行多方面限制选择最优路径，虽然未对传统蚁群算法进行改进，却引入多指标的思维，对解决实际系统运行时产生的问题有很大帮助。

在对上述文献研究分析的基础上，考虑到蚁群算法具有速度快、精度高、寻优能力强且易与其他算法相结合等优点。采用头尾双向搜索策略提高全局搜索能力，加快算法前期搜索效率，提高算法前期有效解。增强寻找全局最优解能力；参考遗传算法中变异思想，引进变异因子，增加算法局部搜索空间；参考狼群算法中“按劳分配”原则对传统蚁群算法信息素改进，引入奖惩因子，通过对最优解的信息素进行奖励，对最差解的信息素进行惩罚，并设立最大最小阈值，使算法跳出局部最优解的能力得到加强；对传统遗传算法引入模拟退火思想，对改进的蚁群算法参数进行优化找到对于本地图模型来说，运行时间最短、路径最少的参数；最后对规划出的路径进行多指标处理，减少路径弯折次数所带来的不必要能耗和时间。

2 环境建模

对AGV小车进行路径优化时需要根据其所处工作环境进行二维空间建模，建模方法通常包括自由空间法、拓扑法、栅格法等[20]。因为栅格地图具有简单有效、易于实现等特点，故而采用栅格法进行建模。将AGV小车的工作环境分为20×20的栅格，并将障碍物进行膨化处理，设AGV 小车为质点。确保小车不会在障碍物边界触碰到障碍物。并根据公式（1）建立栅格地图。若栅格上有障碍物则此栅格为黑色，否则为白色，代表可以通过。如图1所示。在实验平台上设定起始位置（0，0）和

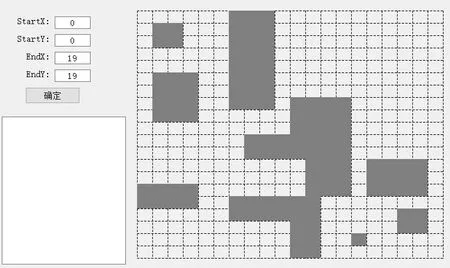
图1 AGV小车路径规划地图模型

终止位置（19，19）。小车共有8个运动方向：北；东北；东；东南；南；西南；西；西北。AGV小车每步可移动步长为1或 2 ，如图2所示。

图2 AGV小车运行方向

3 传统蚁群算法

传统蚁群算法在AGV小车路径规划的应用主要分为觅食规则、信息素规则和移动规则[21]。觅食规则要求设立禁忌表，规定蚂蚁不可行走位置。为避免蚂蚁原地打转，蚂蚁移动后应在禁忌表内加入当前所在位置。

移动规则要求，蚂蚁k 由当前节点i 转移到下一节点j 时的转移概率根据信息素浓度与启发式函数确定，一旦下一步没有可以移动的节点便退出本次查找。为保证路径多样性，假设每只蚂蚁都有犯错的可能，采用轮盘赌法保证小概率节点仍具有被选择的可能，以此加大算法搜索能力。转移概率由式（2）～（4）确定：

信息素规则要求，在蚂蚁运动释放信息素的同时，路径上已存在的信息素按一定比例挥发。蚁群循环一次后，各路径上的信息素按式（5）更新：

式中，ρ 为信息素挥发因子，值为0到1，m 为蚁群数量，为第k 只蚂蚁在当前迭代过程中留下的信息素，如式（6）：

式中Q 为常量，为蚂蚁信息素强度，Lk为蚂蚁k 在本次循环中所走过的路径总长度。

4 改进蚁群算法

4.1 双向搜索机制

传统蚁群算法将蚂蚁全部放置起始点，所有蚂蚁由起始点开始向终止点搜索路径，起始路径大致相同，这样便导致全局搜索能力不足[22]。为此采用将蚁群蚂蚁分为奇偶两组，奇数蚂蚁放置起始点，由起始点向终止点搜索，模拟自然界蚁群寻找食物。偶数蚂蚁放置终止点，由终止点向起始点搜索。模拟自然界蚁群找到食物并运回蚁穴的过程。因此，启发函数应按式（7）（8）改进：

di表示蚂蚁当前位置距离目标点（起始点、终止点）的几何距离。 Ix表示蚂蚁当前位置的横坐标，Iy表示蚂蚁当前蚂蚁位置的纵坐标。Ex表示终止点的横坐标，Ey表示终止点的纵坐标。Sx表示起始点的横坐标，Sy表示起始点的纵坐标。

当两只蚂蚁相遇后便会生成一条新的路径，之后两只蚂蚁继续向各自的目标点移动。两只蚂蚁相遇条件为两者当前坐标的几何距离小于。公式如下：

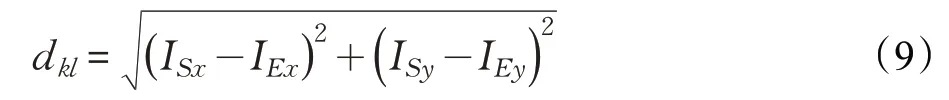
dkl表示起始点出发的蚂蚁与终止点出发的蚂蚁之间距离，ISx代表起始点出发蚂蚁当前横坐标，ISy代表起始点出发蚂蚁当前纵坐标，IEx代表终止点出发蚂蚁当前横坐标，IEy代表终止点出发蚂蚁当前纵坐标。

对蚂蚁转移概率引入变异因子，对转移概率函数进行改进，改进公式如式（10）所示，当随机转移概率大于变异率时，不再选择概率最大的下一节点而是根据当前节点的位置进行随机选择。增大算法的全局搜索能力和跳出局部最优能力。

式中，Pk代表从蚂蚁k 从当前节点i 到下一节点j 的概率代表无变异时的转移概率由式（2）得来。rand代表变异概率，每次转移都会随机生成一个0 到1 范围内的数。 pvar代表变异因子，如果rand 小于变异因子则表明发生变异，当前蚂蚁按改进后的转移概率进行转移。

4.2 引入奖惩因子

传统蚁群算法根据每代最优路径按式（5）进行信息素的更新。因为挥发因子的存在，随着迭代次数的增多，会造成选择区域信息素堆积，未选择区域信息素经过多次迭代其值接近为0，造成信息拥结。不利于全局搜索。因此参考文献[23]中狼群算法，引进奖惩因子，不只对最优路径进行信息素更新，而是采用“论功行赏”策略。对效果最好的路径大幅奖励，对每代最优却非全局最优部分奖励，对最差路径进行惩罚。如式（11）～（14）：

式（11）在式（5）的基础上引入了Δ*τij和Δ**τij两个参数。其中，Δ*τij代表每次迭代最优路径经过节点i、j的信息素大小，由式（13）决定。式中L*表示本代中最优路径长度。Q 为增强因子设为1。并且根据式（12）判断当前最优路径与目前最优路径是否一致，对最优路径进行奖励，Re 代表奖励因子其值在1到2；Δ**τij代表每次迭代最差路径经过节点i、j 的信息素大小，由式（14）决定，式（14）中L**表示本次迭代中最差路径长度。R为减弱因子其值设为0 到1，表示对本次最差路径进行惩罚的系数。

引入最大最小信息素阈值如式（15），避免某路径经过多次迭代后，其上信息素浓度远高于其他路径而导致的搜索停滞，出现早熟收敛。信息素的阈值范围被限定在了τmin到τmax。

4.3 多指标路径规划

对于AGV 小车的路径规划来说，不仅仅需要考虑到路径最短的情况，还要考虑小车运行时间、能耗情况等。小车每次经过拐点都会造成一定的能耗，且对机械磨损也有很大的影响，为此采用多指标方法对适应度函数进行改进。

设小车处于直线状态运行时，忽略加减速时间，假设系统均匀行驶，速度为1 m/s，由于小车每次转弯要根据转弯的角度对行驶方向进行调整，虽然不会停止但仍会对速度有所损耗。为计算方便，现假设每次经过拐点，小车都要停止对行驶方向进行调整。由此可得运行时间表达式如式（16）：

式中，i、j 代表路径Mt中的相连节点，Vt为AGV小车的正常行驶速度。L 为i 节点和j 节点之间几何距离，tw为小车在节点i、j 拐点处转弯所耗费的时间。计算方法如式（17）：

由于AGV 系统移动方向左右角度一致，都为0°、45°、90°和135°四个角度。因此，为简化计算才用四段分段函数表示算法经过拐点所用的时间。式中tω代表每次转弯所耗费的时间，tc代表45°内转弯所耗费的时间，设为常值。w 为转弯角度。对于能耗问题为方便计算定义能耗与时间成正比，综合指标为二者相加。因此运行时间与能耗问题皆可归结为拐点问题。在相同路径下，拐点越多耗时越长、能耗越大。

4.4 遗传算法优化参数

对于传统蚁群算法来说，信息启发式因子、期望启发式因子和挥发函数因子的作用至关重要。信息启发式因子α 的大小反映了信息素因素作用的强度。过大导致全局搜索能力减弱，易陷入局部最优；过小导致算法搜索的随机性增强，收敛速度变慢，难以找到最优路径。期望启发式因子β 反映了先验性、确定性因素作用的强度。过大则导致算法随机性减弱，易陷入局部最优；过小将导致蚂蚁陷入随机搜索，难以找到最优解。挥发函数因子ρ 关系到蚁群算法的全局搜索能力及其收敛速度。过大导致路径残留信息素过少易导致收敛变慢；过小导致信息素过多，全局搜索能力下降导致易陷入局部最优。为此提出利用遗传算法快速、随机的全局搜索能力，对改进的蚁群算法中的重要参数进行优化，通过较优种群的寻找完成蚁群算法参数的优化，优化过程中遗传算法将重复调用蚁群算法，并根据式（18）作为参数优劣的标准：

式中，Mval表示适应度函数值；f( )Mt由式（16）计算得来；iterate 代表算法出现最优解的最少迭代次数；weightm和weighti代表适应度函数和最少迭代数的权重，其值范围0到1。

首先对遗传算法参数进行设定，设定交叉概率、变异概率、种群大小和编码长度。对改进的蚁群算法参数进行二进制处理，设定信息函数因子α 其值范围为0到10；期望函数因子β 其值范围为0 到10；挥发函数因子ρ 其值范围0到1；将它们随机生成一个三维二进制的数组，按式（19）进行十进制处理，带入改进后的蚁群算法中。

按式（18）选择适应度函数最高的种群。之后对种群进行交叉操作和变异操作，生成新种群，以此提高系统的全局搜索能力。之后根据新种群进行选择，最后选择最优的参数，作为本地图模型的参数进行蚁群算法。

由于传统遗传算法易陷入局部最优问题，常常对传统遗传算法引入模拟退火思想[24]。将变异后新种群的最高适应度函数值与交叉变异前的旧种群的最高适应度函数值对比，决定是否生成新种群[25]如式（20）：

式中，f( m )为种群中交叉变异前的适应度，f( n )为交叉变异后的适应度，T 为当前温度，随着进化的进行T按降温速率衰减。计算公式为式（21）：

式中，T0代表退火算法初始温度，q 代表降温速率，t代表进化次数。

4.5 改进蚁群算法流程图

改进的蚁群算法流程图如图3所示。

首先进行环境建模并对蚁群算法参数初始化，将随机生成的参数带入改进后的蚁群算法，判断是否找到目标或将目标送回。如若找到则根据路径优劣对信息素进行更新，否则蚂蚁按概率移动到下一节点，继续寻找目标直到没有下一节点可移动。循环迭代直到寻找到最优路径，记录当前最少迭代次数并按式（18）对适应度进行计算。之后进行选择变异操作，引进模拟退火算法，加强传统遗传算法全局搜索能力。生成新种群。不断循环往复，直至循环结束。

图3 改进蚁群算法流程图

5 结果与分析

为验证改进蚁群算法的有效性，采用VS2017 软件和MATLAB 进行仿真实验，按照公式（1）构建地图模型。为方便计算，仿真所取相关参数如下，遗传算法交叉概率为0.5；变异概率为0.1；种群规模为25；初始温度T0为3 000 ℃；终止温度为0.000 5 ℃；降温速率q 为0.9；蚁群算法蚂蚁数目为50；迭代次数为50；单元格距离为1 m；最小转弯耗时tc=1 s；AGV 小车正常行驶速度Vt=1 m/s；为增加对比性，分析本文算法有效性，分别做了以下几组的对比实验。首先是传统蚁群算法如图4 所示，其次是文献[17]对传统蚁群算法加入自适应参数改进如图5所示。之后是文献[18]采用双向搜索机制对传统蚁群算法改进如图6 所示。最后是本文算法对最短路径进行优化如图7 所示。根据运行时间和能耗情况对系统进行多指标规划如图8 所示。各算法每代最优路径情况如图9 所示。并将四种算法的各类指标列入表1中，进行对比。结果表明本文算法与其他算法相比全局搜索能力有所改进，但收敛速度有待提高。

图4 传统蚁群算法路径

图5 文献[17]算法路径

图6 文献[18]算法路径

图7 本文算法路径

由于本地图特性，若直接采用多指标算法难以体现本文算法优越性。因此，首先根据规划路径的长度作为适应度函数指标进行路径规划。验证本文算法搜索全局能力和跳出局部最优的能力是否有所提高。由图4～7可知，各类算法经过一定次数的迭代皆可以找到一条起点到终点的路径。由传统蚁群算法图4可知，路径陷入了局部最优，寻找到的路径长度为36.970 6 m，明显有更优路径。根据文献[17]对传统蚁群算法进行改进参数优化选择最优的参数进行，如图5 所示，路径长度为34.970 6 m，跳出局部最优能力加强，但全局搜索能力不足。对文献[18]进行改进的蚁群算法，采用双向搜索机制进行路径优化，如图6 所示，路径长度为35.556 3 m，与传统蚁群算法相比跳出局部最优，全局搜索能力皆有所加强，但由于采用相遇即停止策略，使算法加快收敛的同时，对全局搜索能力进行减弱。最后采用本文算法进行路径规划，如图7所示，在评价路径距离时，本文算法效果最好，路径最短为34.384 8 m。证明本文算法在提高全局搜索能力和跳出局部最优解的能力更强。

图8 多指标优化路径

图9 算法比较

除了全局搜索能力外，算法的收敛时间也是评价算法优劣的指标之一。传统蚁群算法、文献[17]改进算法、文献[18]改进算法和本文算法每次迭代的最优路径，如图9所示。

由图9可知，对比传统蚁群算法本文算法在收敛速度方面仍有所提升，但对比文献[17]和文献[18]来说本文算法在加快算法收敛的方面仍有所不足。然而，对于提高算法全局收敛能力跳出局部最优的方面来说，本文算法相较传统蚁群算法、文献[17]和文献[18]具有明显提升。综合对比四种算法指标如最小路径长度、运行时间、拐点数目、能源损耗和最佳迭代次数记入表1。综合对比验证本文算法优越性。

由表1可知，在综合各类指标后本文算法与其他文献算法的对比，易知本文算法在提高全局搜索能力跳出局部最优方面有很大改进。引入多指标进行路径规划时，由于地图特性原因，四种算法在路径优化路线大致相同且迭代次数与图9变化不大，因此不再赘述，仅列出本文算法在多指标条件下对本地图环境的路径规划，如图8所示。路径规划距离为35.799 m，但拐点数仅为7个，运行时间为37.499 s，能源损耗为42.799 W。验证本文算法在兼顾系统运行时间的同时大大减少了能源损耗。

为验证本文算法在复杂环境下的通用性，另外选择两组复杂地图进行实验，一组地图为30×30 复杂情况，根据地图建立模型，由于地图规模扩大，为保证算法可靠性，对蚂蚁数目进行修改，将数目增加至100个，保证算法可以找到路径。传统蚁群算法路径如图10 所示。文献[17]算法路径如图11 所示。文献[18]算法路径如图12所示。由图可知上述算法在复杂地图中都陷入了局部最优。本文算法路径效果图如图13所示。将四种算法在地图二中的各类指标记入表2，验证本文算法的有效性。

图10 地图二传统蚁群算法路径

图11 地图二文献[17]算法路径

图12 地图二文献[18]算法路径

表1 算法指标比较

图13 地图二本文算法路径

由上述可知，传统蚁群算法路径长度为43.941 1 m，文献[17]算法路径长度为42.769 6 m，文献[18]算法路径长度为42.769 6 m，本文算法路径长度为42.183 8 m。

由图14 可知在此复杂地图中，传统蚁群算法最少迭代次数在10 次，收敛速度过慢且陷入局部最优后跳出能力较弱。文献[17]算法最少收敛次数在6 次，可知文献[17]算法在加快收敛速度方面有很大改善，但是对于跳出局部最优情况有待提高。文献[18]最少迭代次数在11次，可知文献[18]算法在提高全局搜索能力有很大提高，但是收敛速度和跳出局部最优能力未有改进。本文算法最少收敛次数在10 次，跟上述算法相比虽然路径最短，跳出局部最优能力有很大改进，但对于加快收敛速度提升不大，有待进一步加强。

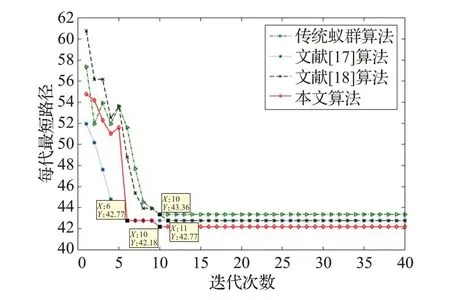
图14 地图二算法比较

由表2 可知本文算法相比较其他算法具有全局搜索能力强和跳出局部最优能力好的优点。

另一组地图为50×50 复杂地图，根据地图建立模型，并将蚂蚁数目增加至150 个，保证算法可以找到路径。传统蚁群算法路径如图15 所示。文献[17]算法路径如图16所示。文献[18]算法路径如图17所示。由图可知上述算法在此地图中同样陷入了局部最优。本文算法路径效果图如图18所示。将四种算法在地图三中的各类指标记入表3。通过对比表明在此复杂地图本文算法仍具有良好的全局搜索能力。

图15 地图三传统蚁群算法路径

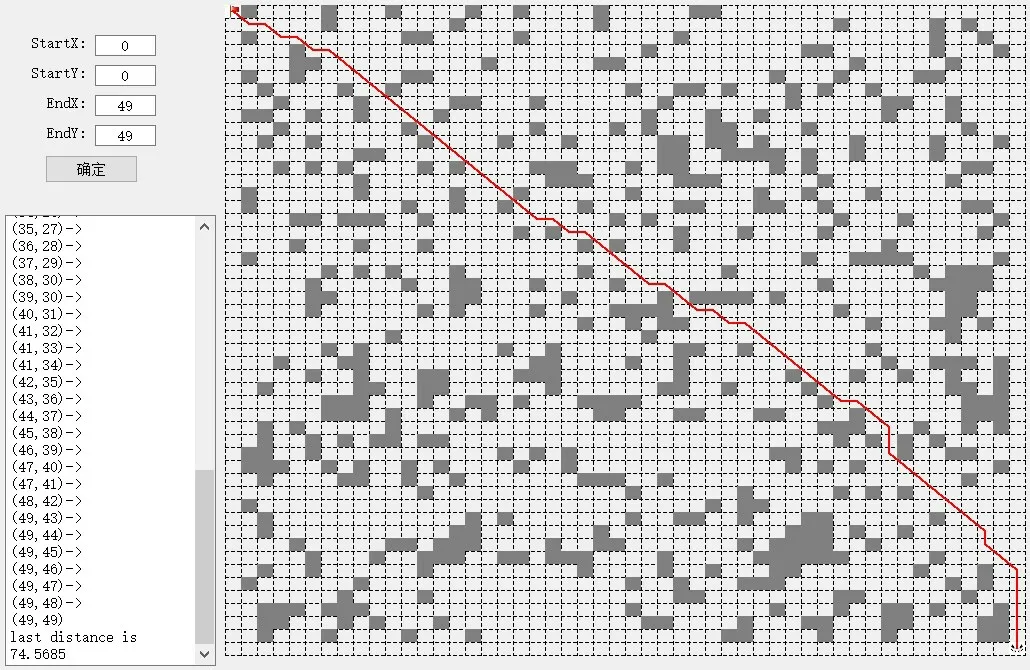
图16 地图三文献[17]算法路径

图17 地图三文献[18]算法路径

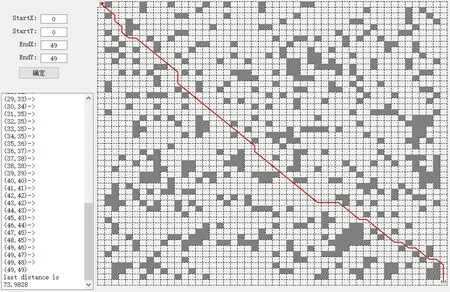
图18 地图三本文算法路径

表2 地图二各算法指标比较

表3 地图三各算法指标比较

由上述可知，传统蚁群算法路径长度为75.982 8 m，文献[17]算法路径长度为74.568 5 m，文献[18]算法路径长度为75.154 3 m，本文算法路径长度为73.982 8 m。验证了本文算法具有良好的全局搜索能力。

由图19 可知在此复杂地图中，传统蚁群算法最少迭代次数在23 次，收敛速度过慢且陷入局部最优后跳出能力较弱。文献[17]算法最少收敛次数在17次，可知文献[17]算法在加快收敛速度方面有很大改善，但是跳出局部最优能力有待改善。文献[18]最少迭代次数在21次，可知文献[18]算法在提高全局搜索能力有很大提高，但是收敛速度和跳出局部最优能力仍有不足。本文算法最少收敛次数在23 次，跟上述算法相比虽然路径最短，跳出局部最优能力有很大改进，但对于加快收敛速度提升不大，有待进一步加强。与之前两种地图仿真结论相同，验证本文算法在各类地图中皆具有良好的全局搜索能力。

图19 地图三算法比较

由表3可知，在复杂地图下本文算法相比较其他算法仍具有良好的全局搜索能力和跳出局部最优的能力，验证本文算法的优越性。

6 结语

针对AGV 小车的路径规划问题，提出了一种改进的蚁群算法，经仿真验证，改进后的算法在路径规划方面是可行的、有效的。本文算法具体有以下特点：

（1）引入双向搜索策略和变异因子，提高蚁群全局搜索能力，加大算法前期搜索有效解的数目，提高算法前期收敛能力，避免算法陷入局部最优解。

（2）引入狼群算法中奖惩因子，对每代蚁群最优个体进行奖励，最差个体进行惩罚，以收敛速度为代价，进一步提高全局搜索能力，避免陷入局部最优。同时设定信息素最大最小阈值，确保不会出现路径信息素接近于0而导致算法陷入停滞。

（3）引入多指标适应度函数，通过对AGV系统的运行时间、能耗情况和拐点数目等评价指标，使规划出的路径更加安全可靠。

（4）采用遗传算法对改进的蚁群算法进行参数优化，为避免遗传算法局部最优问题，引入模拟退火算法加强遗传算法全局搜索能力，保证选择最优参数对算法进行运算，提高算法收敛时间，减少最少迭代次数。