例谈多物体周期性运动时间与空间的统一

王松涛

（中山市华侨中学，广东 中山 528400）

多物体周期性运动的问题是高中物理中最为复杂的内容之一，由于同时运动的物体多、过程多，许多学生在分析时往往顾此失彼，不知所措.而从功和能的角度去分析就更加雾里看花，难辨是非了.

图1

例题.一传送带装置如图1所示，传送带在AB区域是倾斜的，倾角θ＝30°.工作时传送带向上运行的速度保持v＝2m／s不变.现将质量均为m＝2kg的小货箱（可视为质点）一个一个在A处放到传送带上，放置小货箱的时间间隔均为T＝1s，放置时初速度为零，小货箱一到达B处立即被取走.已知小货箱刚放在A处时，前方相邻的小货箱还处于匀加速运动阶段，此时两者相距为s1＝0.5m.传送带装置由电动机带动，传送带与轮子间无相对滑动，不计轮轴处的摩擦，取g＝10m／s2.除了刚释放货箱的时刻，若其他时间内总有4个货箱在传送带上运动，求每运送一个小货箱电动机对外所做的功，并求电动机的平均输出功率P.

图2

解法1：小货箱刚放在A处时，前方相邻的小货箱已经运动了时间T.如图1有代入数据解得加速度大小a＝1m／s2.传送带上总共有4个货箱在运动，说明货箱1在A处释放后经过t＝4T的时间运动至B处.此时，第5个货箱恰要放入A处，如图3，图2为T＝1s前的情景.

图3

货箱在位置D处速度与传送带速度相等，此刻，货箱所受滑动摩擦力突变为静摩擦力，货箱在此后的时间内随传送带做匀速运动，f静＝mgsinθ.传送带克服该货箱的静摩擦力做的功为W2＝f静v（t-t1），代入数据解得W2＝40J.

每运送一个小货箱电动机对外做的功为W＝W1＋W2＝88J.

放置小货箱的时间间隔为T，则每隔时间T就有一个小货箱到达B处，因此电动机的平均输出功率为88W.

对于解法1，很多学生感到迷惑.货箱1从A处运动到B处的4s时间内，电动机不是同时在对货箱2、3、4做功吗？为什么解答中只计算了电动机对货箱1做的功，而并未计算对货箱2、3、4做的功呢？另外，运送一个货箱的时间明明是4s，即电动机对一个货箱做功的时间为4s，为什么计算电动机输出功率时这个时间却又取1s呢？

分析：首先，运送一个货箱对应的时间是1s而非4s.因为观察者在B处每隔1s就可取得1个货箱，这与该货箱是何时放上去的并无关系.其次，电动机对货箱1做功的同时，很明显对货箱2、3、4也做了功.题目中要求每运送一个小货箱的过程中电动机对外所做的功，显然，更直接地看应是求在1s的时间内，电动机对货箱1、2、3、4所做的总功.那么，为何答案中却是求电动机对一个货箱在4s内所做的功呢？

现在，我们来分析4个货箱同时做周期性运动的特点.货箱1在4个连续的1s内的运动分别经历了A→C、C→D、D→E和E→B等4个过程，而货箱1、2、3、4在1s内的运动为货箱4经历了A→C，货箱3经历了C→D，货箱2经历了D→E，和货箱1经历了E→B的4个过程.即货箱1在4s内的运动恰好是经历了货箱1、2、3、4在1s内所经历的过程.故电动机对货箱1在连续4s内所做的功应等于电动机在1s内对连续4个货箱所做的功.因此用电动机在1s内对4个货箱所做的功来验证.

解法2：在从图2到图3的1s内，货箱1和2受静摩擦力作用，而货箱3和4受滑动摩擦力作用.电动机克服4个货箱的摩擦力做功为W＝（2f滑＋2f静）vT＝88J.

结论：解法1和解法2的一致性正好说明了多物体周期性运动时间和空间的统一.

以上从摩擦力做功的角度验证了多物体周期性运动时间和空间的统一，还可以变换角度，从功是能量转化的量度出发，用能量转化这个更本质的视角来探讨这一问题.

货箱放到传送带上，电动机多做的功对应于多消耗的电能，而电动机多消耗的电能使得货箱的机械能增加，同时，货箱与传送带摩擦产生了内能.

解法3：从图2到图3的一个T内，电动机对外做的功等于1、2、3、4共4只货箱动能的增加、重力势能的增加和货箱3、4与传送带之间滑动摩擦产生内能的总和.

系统增加的动能为ΔEk＝Ek′-Ek.

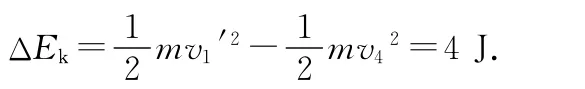
系统增加的重力势能为ΔEp＝Ep′-Ep.

Ep′＝mg·AC·sinθ＋mg·AD·sinθ＋mg·AE·sinθ＋mg·AB·sinθ，

Ep＝mg·AC·sinθ＋mg·AD·sinθ＋mg·AE·sinθ.故ΔEp＝mg·AB·sinθ＝mg（·2T＋v·2T ）sinθ＝60J.

由图2到图3的一个T内，货箱1和2匀速运动，不会摩擦生热.

货箱3与传送带相对滑动的路程为

货箱4与传送带相对滑动的路程为

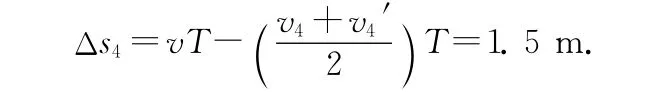
故ΔE内＝f滑·Δs3＋f滑·Δs4＝24J.

图2到图3的一个T内，4个货箱和传送带总的能量变化为ΔE＝ΔEk＋ΔEp＋ΔE内＝88J.故电动机对外做功为88J.

那么一只货箱在从A处运动到B处的4s时间内，能量变化又如何呢？

解法4：一只货箱在从A处运动到B处过程中其能量变化为

货箱在前2s内相对于传送带滑动的路程为

可得ΔE＝ΔEk＋ΔEp＋ΔE内＝88J.故电动机对外做功为88J.

从能量转化的角度我们再次验证了多物体周期性运动时间与空间的统一性.

结论：多物体周期性运动具有物体多、过程多等复杂性，但却具有空间与时间周期性统一的规律.以上4种解法都体现了这一特点，如果能很好地利用这一点，就能化繁为简，举重若轻.例如本题中解法2和解法4相对于解法1和解法3就更为简单明了.