例析牛顿第二定律应用之临界问题的解题思想和方法
刘 玲
(复旦大学附属中学,上海 200433)
1 立足基础 —— 掌握临界问题的思路和方法
我们先来看一下2012年上海高考第30题,通过这道题目来讨论解决临界问题的基本思想和方法.

图1
例1.(2012年上海卷)如图1,将质量m=0.1kg的圆环套在固定的水平直杆上.环的直径略大于杆的截面直径.环与杆间动摩擦因数μ=0.8.对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环以a=4.4m/s2的加速度沿杆运动,求F的大小.

图2
解析:对圆环进行受力分析,临界条件为杆对圆环的弹力为0,此时受力分析如图2所示.此时,满足Fsinθ-mg=0,得F=N=1.25N.

图3
(1)当F<1.25N,时,环与杆的上部接触,受力分析如图3所示.根据牛顿第二定律,

联立(1)、(2),有
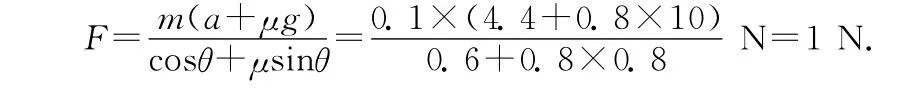
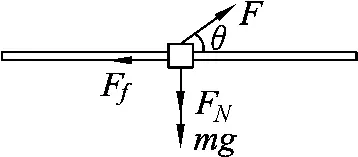
图4
(2)当F>1.25N,时,环与杆的上部接触,受力分析如图4所示.根据牛顿第二定律,
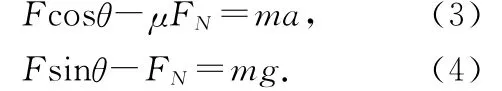
所以有

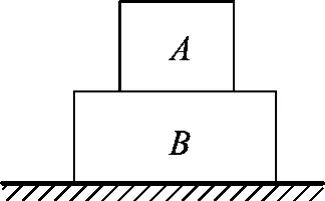
图5
例2.质量分别为mA和mB的两个物体A、B叠放在光滑水平桌面上,如图5所示当用某一水平力拉B时,A、B两物体恰好能一起以加速度a1做匀加速运动,那么如果在A上加一水平力,要使A、B之间不发生相对运动,水平力不能大于多少?
解析:用水平力拉B时,A是依靠B给它的静摩擦力产生加速度的,所谓恰好能一起以加速度a1做匀加速运动,也就是说如果水平力再大的话,A、B之间就要发生相对运动了,所以临界条件是此时A、B之间的摩擦力达到最大值.对A物体应用牛顿第二定律,可以得到A、B之间的最大静摩擦力为fm=mAa1.
当一水平力加在A物体上时,B是依靠A给它的静摩擦力产生加速度的,所以临界条件是此时A、B之间的摩擦力达到最大值.设此时的加速度为a2,对B物体应用牛顿第二定律,有fm=mBa2.所以得到a2=.对A、B 整体应用牛顿第二定律,有

从对上述两道题目的分析我们发现,在动力学中,接触与脱离的临界条件是弹力等于0,相对静止的临界条件是静摩擦力达到最大值,解决临界问题要牢牢抓住这个关键点.
2 综合应用——与连接体问题的结合
在动力学中临界问题经常和比较复杂的连接体问题一起出现,除了要掌握临界问题的关键点,还要注意连接体问题中整体法和隔离法的使用.
(1)连接体的系统中有两个物体.

图6
例3.两个质量都为m的滑块A和B,紧挨着并排放在水平桌面上,A、B间的接触面垂直于图6中纸面与水平面成θ角,所有接触面都光滑无摩擦.现用一个水平推力F作用于滑块A上,使A、B一起向右做加速运动,如果要使A、B间不发生相对滑动,水平推力的大小在什么范围内?
解析:首先应用整体法,把A、B看做一个整体,在水平推力F作用下,A、B共同加速运动,则

然后利用隔离法,分别隔离A,B,受力分析如图7所示,FTA、FTB为A、B间相互作用的弹力,与斜面垂直.FNA、FNB分别为地面A、B作用的弹力,与地面垂直.
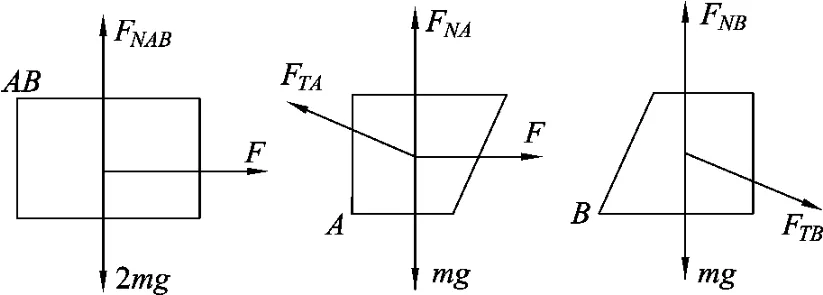
图7
对A列方程

对B列方程

接下来分析物体的临界状态.注意,这道题目的临界条件比较隐蔽,对物体的受力情况列出方程后,要一步一步仔细分析,从而找出临界条件.
由(1)式可知,当F增大时,a增大.由(4)式可知,a增大时,FTB增大,则FTA也增大.由(3)式可知,FTA增大,FNA减小.
通过上面的分析,A、B间不发生相对滑动的临界条件为FNA=0,即A与地面分离.设此时对应的加速度为a0,当加速度大于a0时,则FTAcosθ>mg,A具有竖直向上的加速度,A被挤离地面.
当FNA=0时,对A有FTAcosθ=mg,对B有FTBsinθ=ma0,解得a0=gtanθ.对整体而言,F=2ma0,可得F=2mgtanθ.所以F的取值范围是0≤F≤2 mgtanθ.
(2)有多个物体的连接体系统.
当系统内有多个物体时,巧妙选取研究对象就显得非常重要了.看下面的题目.

图8
例4.光滑水平面上放置质量分别为m和2 m的4个木块,其中两个质量为m的木块间用一不可伸长的细绳相连,木块间的最大静摩擦力是μmg,如图8所示.现用水平拉力F拉其中一个质量为2 m的木块,使4个木块以同一加速度运动,求轻绳对m的最大拉力T和F的最大值.
解析:这道题目物体比较多,可以通过巧妙地选取研究对象来解决问题.
首先,从木块间的静摩擦力入手.对上面的两块木块和左下方的木块这3块木块来说,它们在水平方向上的合外力为右上方木块和右下方木块之间的静摩擦力,所以此题的临界状态为右上方木块和右下方木块之间的静摩擦力达到最大值,为μmg,设此时上面的两块木块和左下方的木块这3块木块整体的加速度为a0.根据牛顿第二定律,有μmg=(m+m+2 m),得
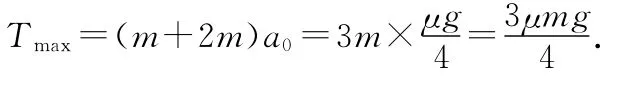


图9
例5.光滑的圆球恰好放在木块的圆弧槽内,它们的左边接触点为A,槽半径为R,且OA与水平面成α角.球的质量为m,木块的质量为M,木块所处的平面是水平的,各种摩擦及绳、滑轮的质量都不计,如图9所示.求释放悬挂物P后,要使球和木块保持相对静止,P物的质量的最大值是多少?

图10
解析:首先应用隔离法,对圆球进行受力分析(如图10所示).我们发现临界条件是:当二者即将发生相当运动时,圆球会绕A点翻转.临界状态圆球的受力分析如图10所示,根据牛顿第二定律,有



由(1)式得,α≤45°时,小球发生相对运动的加速度a>g,故当α≤45°时,球和木块不会发生相对运动.
若α>45°时,由(1)、(2)式得,


从上面的分析可知,在临界问题的课堂教学中,教师通过讲解,首先应该使学生学会解决临界问题的基本方法,然后还要使学生体会与其他问题的结合(如连接体问题).在这样的过程中使学生逐渐深入理解问题的本质,让学生学会融会贯通、比较鉴别和综合归纳.这对提高学生的学习积极性、提高解题能力和培养创新思维是大有裨益的.
1 李品忠.复旦大学附属中学高三物理总复习讲义(力学分册)[M].上海:复旦大学出版社,2010.
2 陈海燕.牛顿第二定律的几类典型应用[J].中学物理,2013(9).
3 朱浩.龙门专题·高三力学[J].北京:龙门书局,2011.
4 高成军.谈高一教学中牛顿第二定律结合临界问题的难点突破[J].物理教师,2011(9):14-16.

