SOLO分类理论助力中考数学评价创新
裘建龙
【摘 要】 开放性试题已成为当前教育改革的一个亮点和热点,而采用传统的“采点给分”法来赋予学生试题的分值,只有利于考查学生思维能力的類型,却无法考查学生思维能力的层次。SOLO分类理论可以客观地评价开放性试题,为检测学生的数学高级思维能力提供了一个切实可行的思路。
【关键词】 SOLO分类理论 开放题 中考评价 学生提问
近年来兴起的SOLO分类理论力求解决的就是考查评价学生思维能力的层次问题。笔者结合在阅卷过程中的感触,以2018年绍兴中考数学卷23题第3问的结论开放性问题为例,探讨运用SOLO分类理论,对学生的学习效果做出分类评价分析。
一、SOLO评价理论依据
SOL0评价理论依据学生在学习过程中通过对学习任务的不同表现,将学生的学习效果由低到高划分为五种结构水平,具体如下:
1. 前结构水平:学生基本上无法理解问题和解决问题,只提供了一些逻辑混乱、没有论据支撑的答案,简单的问题都不能得以解决,甚至被其他方面所误导,从而导致无法解决问题,对于学习任务根本不能完成。
2. 单一结构水平:学生找到了一个解决问题的思路,但却就此收敛,单凭一点论据就跳到答案上去,不能全面地观察学习任务中各种内容之间的联系,在找到一个答案后便急于下结论。
3. 多元结构水平:学生找到了多个解决问题的思路,但是他们还不能发现或掌握它们彼此之间的关联,无法对其进行有效的整合利用,只是给出一些零散的信息。
4. 关联结构水平:学生找到了多个解决问题的思路,并且能够把这些思路结合起来思考,通过联想,将这些事件联系起来,达到能够解决复杂问题的程度,同时还能发现自己学习过程中的错误并予以改正。
5. 拓展抽象结构水平:学生能够对问题进行抽象的概括,从理论的高度来分析问题,而且能够深化问题,使问题本身的意义得到拓展,在归纳总结问题中概括了新的和更抽象的特征本质,这样得出来的结论具有开放性,更深一层次地拓展了问题本身的意义。学生达到这个层面便会更有创新精神和钻研意识。
二、SOLO评价理论在中考数学评析中的应用
数学这门学科对学生有着独特的思维要求,就是在解题过程中要有缜密的分析性和严谨的条理性。现在我们通过2018年绍兴中考数学试卷23题第3问的实例分析,研究S0LO评价理论在中考数学评价中起到的积极导向作用。
2018年绍兴卷23题:小敏思考解决如下问题:
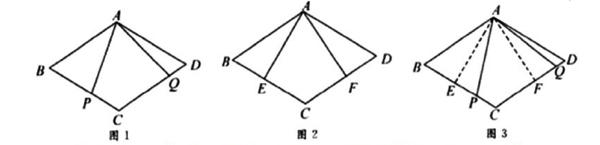
原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.
(1) 小敏进行探索,若将点P,Q的位置特殊化:把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E,F分别在边BC,CD上,如图2,此时她证明了AE=AF.请你证明.
(2) 受以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F.请你继续完成原题的证明.
(3) 如果在原题中添加条件:AB=4,∠B=60°,如图1. 请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分)。
如果将考生提出的问题按SOLO分类评价理论的五个学习水平来分析,则可以得到一个评价“考生提出的问题”的五个层次结构,可以将考生回答此问题的思维层次进行如下划分,并赋予不同的分值:
l. 前结构水平:考生提出的问题表述混乱让人无法理解或者提出的问题与供给的素材无关。这是最低级的水平,可认为考生不能阅读理解所供给的素材和不具有提出问题的能力。考生进行答题无效,这样的情况下只能得0分。
2. 单一结构水平:考生提出的问题是关于单一术语层面的是什么的再现型浅层问题。说明考生是在进行机械记忆式的浅层学习,所提出的问题既不广也不深,这样的答案得1分。例如:
① 求∠D的度数. 答案:∠D=60°.
② 分别求∠BAD, ∠BCD的度数. 答案:∠BAD=∠BCD=120°.
③ 求菱形ABCD的周长. 答案:16.
④ 分别求BC, CD, AD的长. 答案:4, 4, 4.
3. 多元结构水平:考生提出的问题,包括了多个术语的是什么的再现型浅层问题,但只是简单罗列这些术语,这些术语似乎是相互独立的。说明考生依然是在进行机械记忆式的浅层学习,但考生在学习中能找到越来越多的术语,然而却并未理解这些术语之间的关系,不能将它们有机整合起来,这样的答案得2分。例如:
① 求PC+CQ的值. 答案:4.
② 求BP+QD的值. 答案:4.
③ 求∠APC+∠AQC的值. 答案:180°.
4. 关联结构水平:考生提出的问题包括了多个术语,并且重点涉及这些术语内部要素之间联系。说明考生能在要点的内外间联系层面上,力图通过提问和对问题的思考将供给素材理解整合为一个有机整体,对供给素材有一个整体意义。这一层次表明考生通过深度学习真正理解了供给素材,这样的答案得3分。例如:
① 求四边形APCQ的面积.答案:4√3.
② 求△ABP与△AQD的面积和.答案:4√3.
③ 求△APQ的面积最小值.答案:3√3.
5. 拓展抽象结构水平:考生能将关联的结构整体概括到一个更高的抽象水平,并使用这种概括在一个新的主题或领域提出拓展性问题,这一层次的考生表现出很强的创新意识。例如:
① 求四边形APCQ周长的最小值.答案:4+4√3.
② 求PQ中点运动的路径长.答案:2√3.
③ 求的最小值.答案:14.
三、对SOLO评价理论在中考数学评价中运用的思考
SOLO分类评价理论认为考生对每个问题的回答,可分为五个结构水平,这五种水平按照层次逐步提升,构成了一个学习水平连续发展的整体,从前结构水平到单一结构水平到多元结构水平是量变,而从多元结构水平到关联结构水平到拓展抽象结构水平则是质的变化。
SOLO分类评价理论,最重要的作用是,它可以详细地分层列出考生的思维水平。中考中运用了这种评价方法,阅卷老师能够根据考生的知识水平、考生的思维层次以及考生的解题表达,给考生的答卷赋予相应的分值。
总之,SOLO分类评价理论给我们提供了新的分析数学思维能力的视角和方法。该理论不是以分析思维的种类为目标,而是以分析思维的层次为目标,由于所有的思维问题都存在层次的高低,因此在实践中这种理论是切实可行的。
参考文献
[1] 百度百科:SOLO分类理论词条.
[2] 兰党军.SOLO评价理论在高中数学教学中的应用.理论与实践周刊,2016(3).

