NSD 序列生成的移动平均过程的矩完全收敛性

高云峰，邹广玉

（1.吉林农业科技学院电气与信息工程学院，吉林吉林132101； 2.长春工程学院 理学院，吉林长春130012）

0 引言及主要结果

NA 随机变量最早由JOAG-DEV 等[1]提出，在可靠性理论、渗透理论及多元分析中有广泛的应用[2]。HU[3]最早在超可加函数的基础上引入了NSD随机变量，并举例说明 NSD 推不出 NA。CHRISTOFIDES 等[4]进 一 步 指 出,NA 能 推 出NSD，表明NSD 序列是包含独立和NA 序列在内的一类很广泛的相依序列。HU[3]进一步举例说明椭球等高分布、排列分布、多项分布、多元超几何分布、Dirichlet 分布等在一定条件下都具有NSD 序列的性质，因此，研究NSD 序列的极限性质具有一定意义。关于NSD 序列的最新成果可参见文献[5-9]。

定义1[1]如果对于集合(1,2,…,n)的任何2个不相交的非空子集A 与B，都有

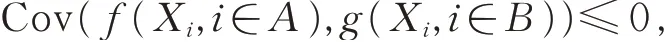
其中f 与g 是任何2 个使协方差存在且对每个变元均非降(或同为对每个变元均非升)的函数，则称随机向量X =(X1,X2,…,Xn)为负相协的(negatively associated, 简 称NA)。 如 果 对 于 任 意 的n ≥1,(X1,X2,…,Xn) 为NA 的，则 称 随 机 变 量 序 列{ Xn,n ≥1}为NA 的。

定义2[3]如果对任意的x=(x1,x2,…,xn)，y=(y1,y2…,yn)∈Rn有

其中，x ∨y=(max(x1,y1),…,max(xn,yn))，x ∧y=(min(x1,y1),…,min(xn,yn))，则称函数φ:Rn→R 为超可加的。

定义3[3]如果满足

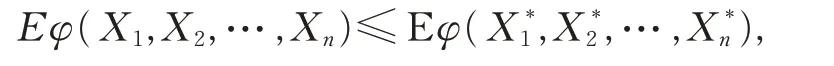
其中，X*1,X*2,…,X*n为相互独立的随机变量，且对任意的i,X*i和Xi有相同的分布，φ 为超可加函数且期望存在，则称随机向量X =(X1,X2,…,Xn)为负超可加相依的（negatively superadditive dependent,简称NSD）；如 果 对 于 任 意 的n ≥1,(X1,X2,…,Xn) 为NSD 的，则称随机变量序列{ Xn,n ≥1}为NSD 的。

定义4如果对任意的λ＞0，满足

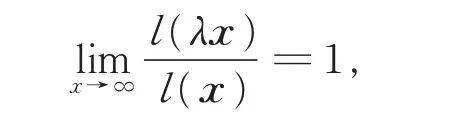
则称定义在[ A,∞)上的实值正函数l(x)为在无穷远处的缓变函数。

定义5如果存在正常数C，使得对所有的x ≥0,-∞＜i ＜∞，有

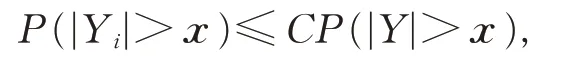
则称{Yi,-∞＜i ＜∞}为被随机变量Y 控制的随机变量序列。

完全收敛是概率极限理论研究的热点之一，最早由HSU 等[10]提出，自21 世纪初以来，众多学者对NSD 序列的收敛性进行了研究[11-19]，但大多是关于部分和加权和的，由NSD 序列生成的移动平均过程的矩完全收敛性的研究至今未见，为此，笔者进行了初步研究，得到以下主要结果：

定 理1设p ≥1,α ＞1/2,{Yi,-∞＜i ＜∞}为被随机变量Y 控制的NSD 随机变量序列，满足当1/2 ＜α ≤1,EYi=0 并 且 当 p ＞1 时 ，E|Y|pl(|Y|1/α)＜∞,当p=1 时，E|Y|1+δ＜∞，对某个δ ＞0，其中l 为在无穷远处的正值缓变函数，记{ai,-∞＜i ＜∞}为一绝对可和的实数序列，Xn=，那么对任意ε ＞0，有

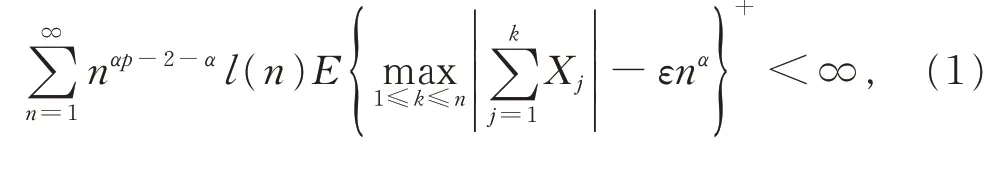
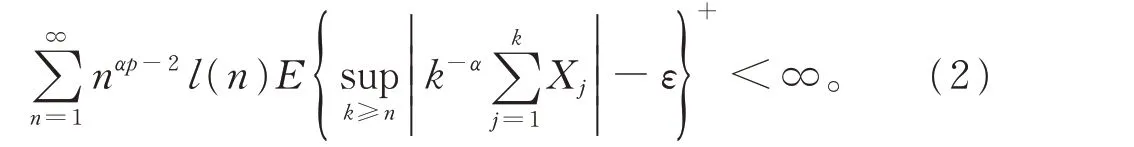
定理2设1≤p ＜2,{Yi,-∞＜i ＜∞}为被随机变量Y 控制的NSD 随机变量序列，满足EYi=0 和E|Y|pl(|Y|p)＜∞，其中l 为在无穷远处的正值缓变函数，设{ai,-∞＜i ＜∞}为一实数序列，满足其 中，当 p=1 时，θ ∈(0,1)，当p ∈(1,2)时，θ=1。记那么，对任意ε ＞0，有

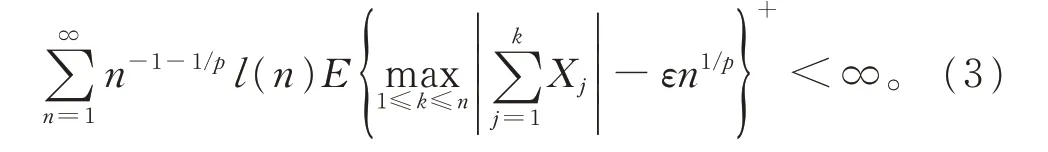
由上述矩完全收敛性可立即得到：

推论1在定理1 的假设条件下,对任意ε ＞0，有

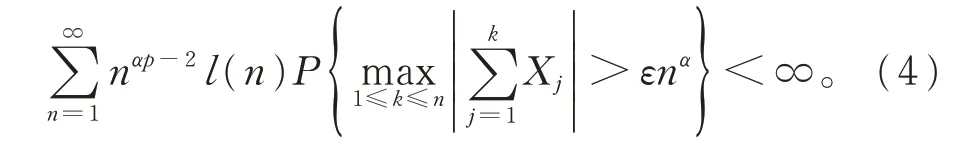
在定理2 的假设条件下, 对任意ε ＞0，有

特别地，当EYi=0 和E|Y|p＜∞时，可推得Marcinkiewicz-Zygmund 强大数定律，即

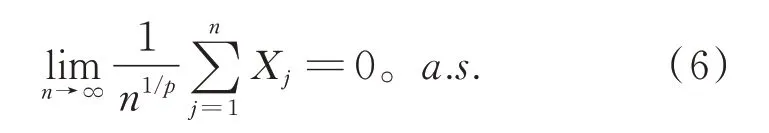
注1令a0=1,ai=0,i ≠0，显然{ai}绝对可和且Xn=Yn，因此，上述定理和推论对NSD 序列的部分和也成立。推论1 中的式(4)推广 了 文献[12]中的定理3.1，从1≤p ＜2,α ＞1/2,αp ＞1 推广到p ≥1,α ＞1/2,αp ＞1；式（5）即为文献[12]中的定理3.2。所以本文推广了已有的结论。

注2如果{Yi,-∞＜i ＜∞}是同分布的NSD 随机变量序列，那么，定理1、定理2 和推论1 仍成立。

注3由于NSD 序列包含独立和NA 序列，因此，定理1、定理2和推论1 对独立和NA 序列仍然成立。从而本文将文献[20-21]中从独立和NA 序列的结论推广至NSD 序列。

1 定理的证明

在本节中，C 表示正常数，不同的地方可表示不同的值。首先介绍在证明过程中要用到的几个引理。

引 理1[2]如 果(X1,X2,…,Xn) 是NSD 的，g1,g2,…,gn都 是 非 降 函 数 ，那 么 (g1(X1),g2(X2),…,gn(Xn))也是NSD 的。

引理2[11]设{Yi,i ≥1}为一零均值的NSD 随机变量序列，满足E|Yi|p＜∞,其中p ≥2。那么存在正常数Cp，使得

引理3[22]如果l 是一缓变函数，那么

(1)对任意的s ＞-1 和正整数m,有

(2)对任意的s ＜-1 和正整数m,有

引理4[23]设随机变量序列{Yi,-∞＜i ＜∞}被随机变量Y 控制，那么对任意的a ＞0,b ＞0，-∞＜i ＜∞，存在正常数C1，C2，使得

定理1 的证明首先证明式（1）。记

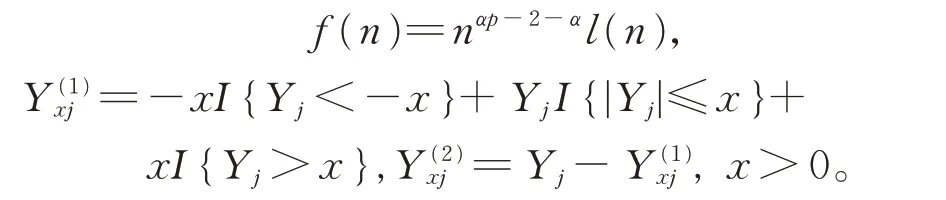
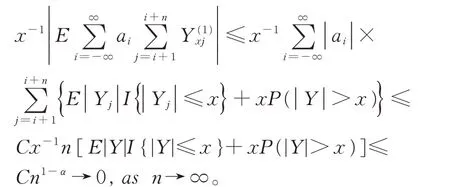
若1/2 ＜α ≤1，注意到αp ＞1，这意味着p＞1。由题设条件E|Y|pl(|Y|1/α)＜∞和缓变函数的性质可知，当0 ＜ε ＜p-1/α 时，有E|Y|p-ε＜∞。再 注意到EYi=0,由引理4 可推得

因此当x ＞nα充分大时，

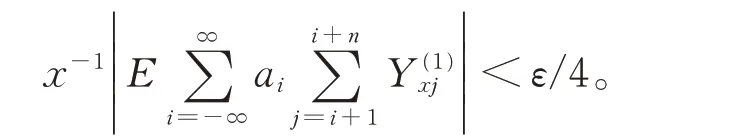
从而

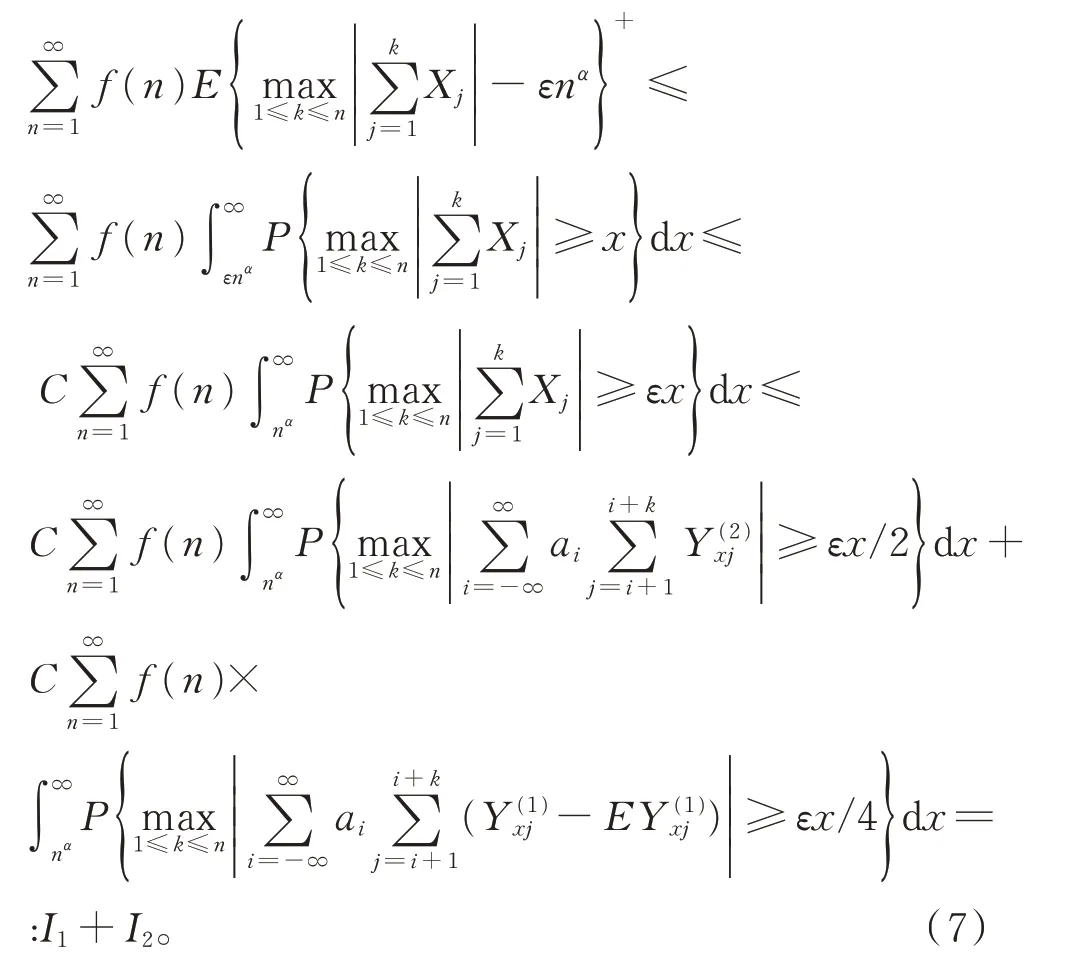
接 下 来 证 明 I1＜∞。 注 意 到 |Y(2)xj|＜|Yj|I {|Yj|＞x }，由Markow 不等式和引理4 知，

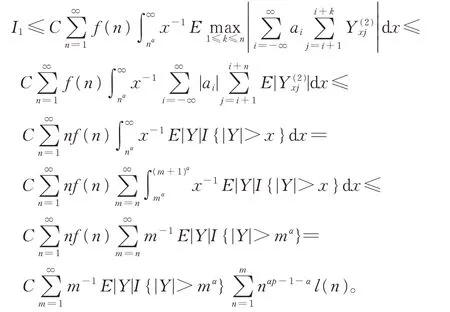
如果p＞1,则αp-1-α ＞-1,由引理3 知,

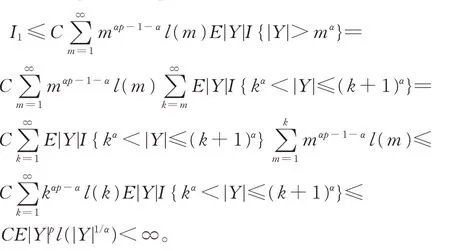
如 果p=1，注 意 到 对 任 意 的0 ＜δ′＜δ，由E|Y|1+δ＜∞, 可 知 E|Y|1+δ′l(|Y|1/α)＜∞，由 引理3 知,

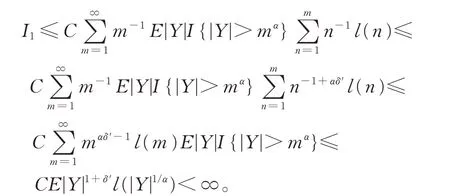
由上述讨论可知，

下 证I2＜∞。由Markow 不 等 式、Ho¨lder 不 等式、引理2，对某个r ＞2 有

对于I21，如果p ＞1，取r ＞max {2,p}，由Cr 不等式、引理3 和引理4 知，

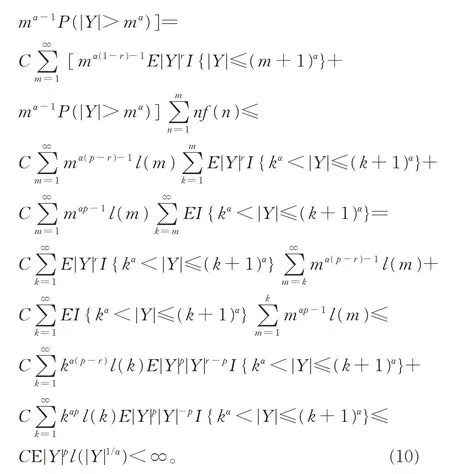
对 于I21，如 果p=1，取r ＞max {1+δ′,2}，其中0 ＜δ′＜δ。类似式（10）的证明，可知

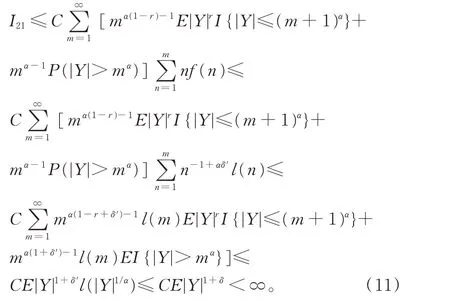
对于I22，如果1≤p ＜2，取r ＞2，注意到αp+r/2-αpr/2-1=(αp-1)(1-r/2)＜0，由Cr 不等式、引理3 和引理4 知，

对 于 I22，如 果 p ≥2 取 r ＞(αp-1)/(α-1/2)＞2，易推得α( p-r)+r/2-2 ＜-1，类似式（12）的证明过程，可知

联立式（7）～（13），可知式（1）成立。

接下来证明式（2），由引理3 和式（1）可知,

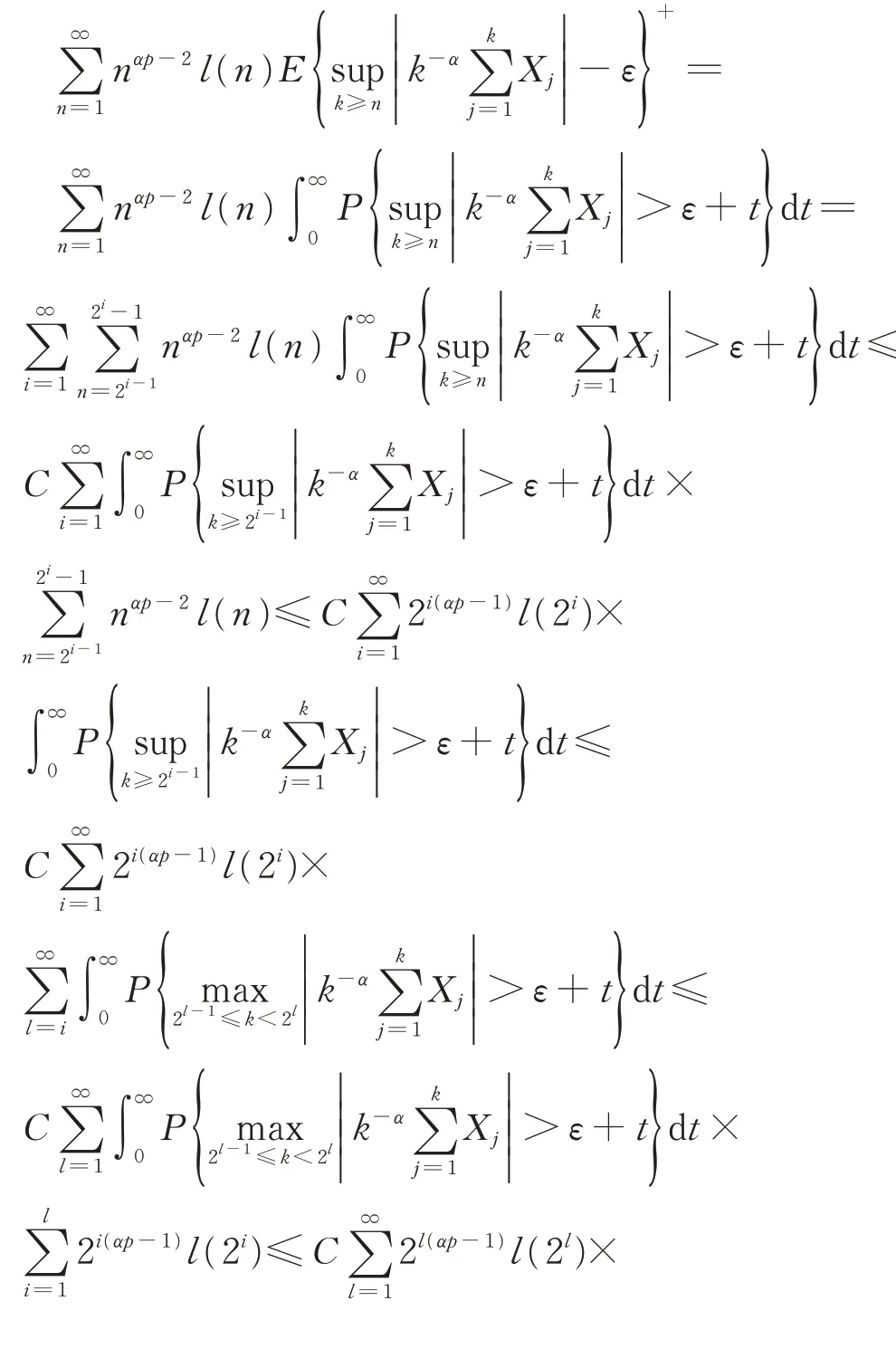
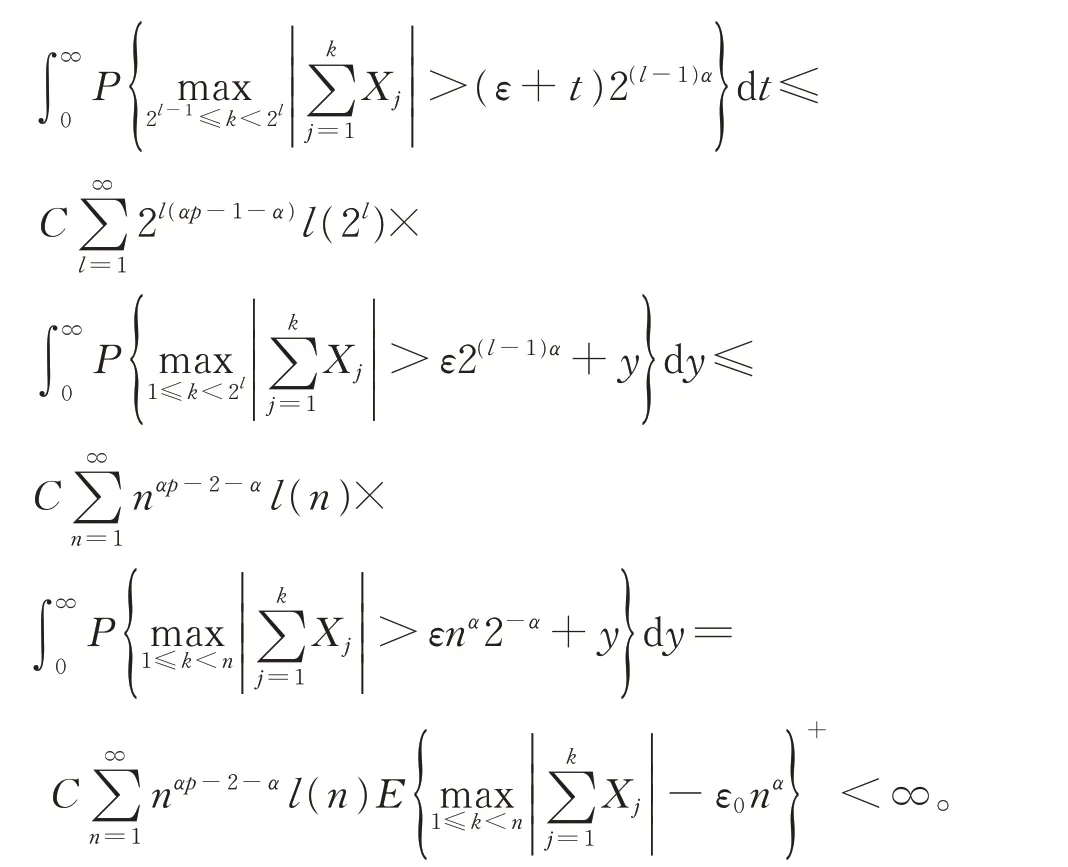
定理1 证毕。

定理2 的证明和定理1 式（1）的证明类似，此略。