广义矩阵代数上的一类局部非线性三重可导映射

费秀海，戴磊，朱国卫

（1.滇西科技师范学院 数理学院，云南 临沧677099； 2.渭南师范学院 数学与统计学院，陕西 渭南714099）

1 预备知识

设Α 是含有单位元的交换环R 上的一个代数,P 为Α 中 的 一 固 定 元,是Α上的一个可加(或无可加性假设)的映射。若对任意的X ∈Α 且2X =0, 有X =0, 则称Α 是2-无挠的。若对任意的X,Y ∈Α 且XY =P, 有

则称δ 是一个P 点可导映射(或P 点非线性可导映射)；若对任意的X,Y ∈Α 且XY =P, 有

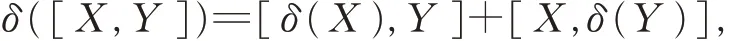
则称δ 是一个P 点Lie 可导映射(或P 点非线性Lie可导映射)；若对任意的X,Y,Z ∈G 且XYZ ∈Ω, 有

则称δ 是一个局部三重可导(或局部非线性三重可导)映射。

近年来,算子代数上各种类型的映射吸引了研究者的兴趣,并成为了算子代数研究领域的热点问题。文献[1-3]分别研究了套代数、三角代数、广义矩阵代数上的全可导点、Jordan 高阶全可导点及交换零点Jordan 可导映射；文献[4-5]刻画了素环和B(Χ)上的非线性Lie 可导映射；文献[6-10]主要研究了三角代数上的Lie 导子、非线性Lie (高阶Lie)可导映射、非线性广义Lie 可导映射；文献[11-12]将非线性和局部非线性结合起来研究了上三角矩阵代数和全矩阵代数上的非线性零点可导映射。特别地, 孟利花等[13]研究了三角代数上的局部非线性三重可导映射。本文主要研究广义矩阵代数上的局部非线性三重可导映射。

下文中将用到的关于广义矩阵代数的基本概念及性质介绍如下：

设Α 和Β 是含有单位元的交换环R 上的代数,Μ 是 忠 实(Α,Β)-双 边 模, Ν 是 忠 实(Β,Α)-双 边模, 则

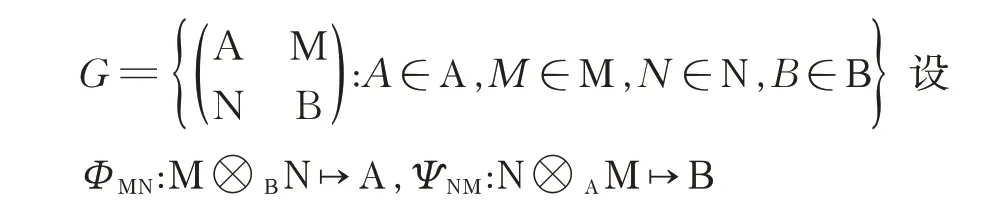
是双边模同态,且满足交换图:

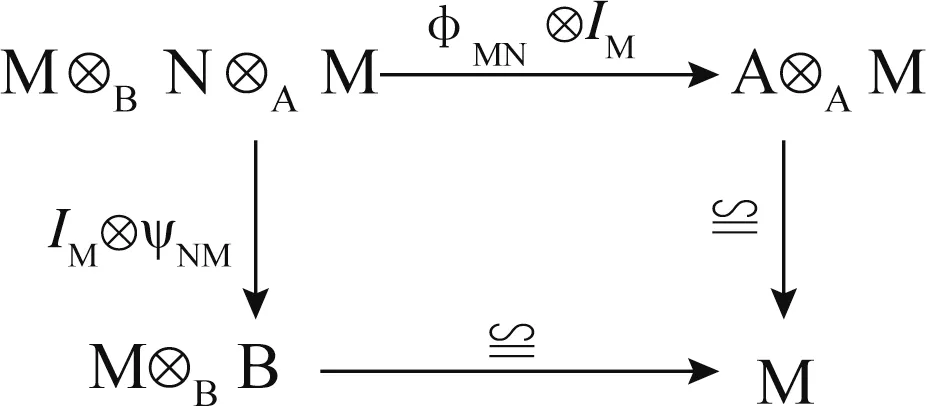
和

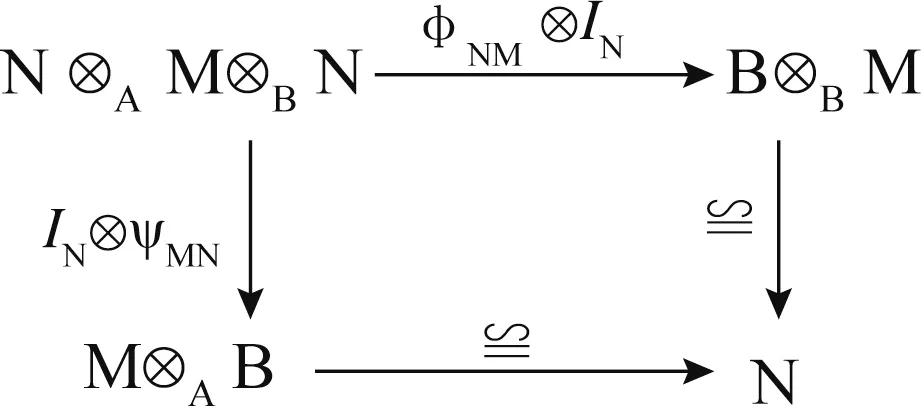
则按矩阵通常的加法和乘法运算构成结合代数，称G 是一个广义矩阵代数。当Ν=0 时,称G 是一个三角代数。

设1Α和1Β分别为代数Α 和Β 中的单位元, 1 是广义矩阵代数G 中的单位元。

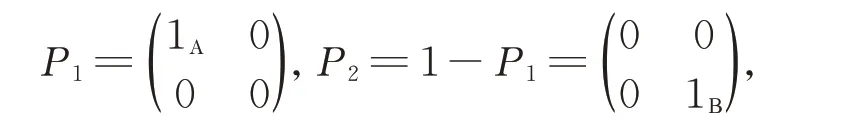
由 于 G11=P1GP1, G12=P1GP2，G21=P2GP1，G22=P2GP2是G 的子代数且分别同构于Α, Μ,Ν和Β, 从而广义矩阵代数G 在双模同构意义下可被分解为

进而对任意的矩阵X ∈G, 可将X 分解成

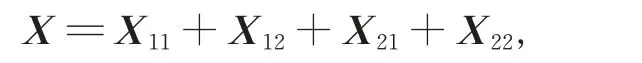
其中，Xij∈Gij, 1≤i,j ≤2 。

2 主要结论及证明

定理1设G 是一个2-无挠的广义矩阵代数,Ω={T ∈G:T2=0}，且φ 是G 上 的 一 个 映 射(无 可加性假设), 若对任意的X,Y,Z ∈G 且XYZ ∈Ω, 有

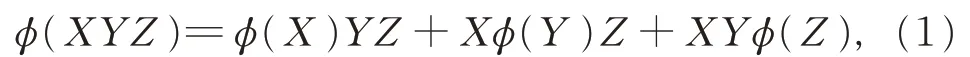
则φ 是一个可加的导子。

为证定理1, 需要以下引理。

引理1对任意的1≤i ≠j ≤2,有

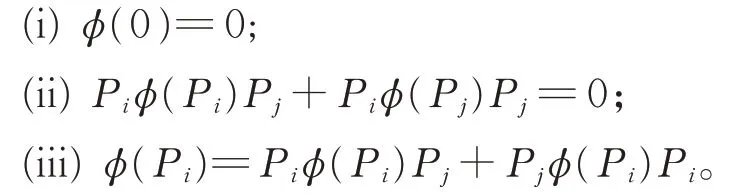
证 明在 式(1) 中, 令X =Y =Z=0, 有φ(0)=0。在 式(1)中,令X =Y =Pi，Z=Pj(1≤i ≠j ≤2), 则有

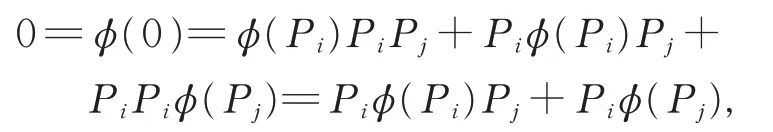
进而可得

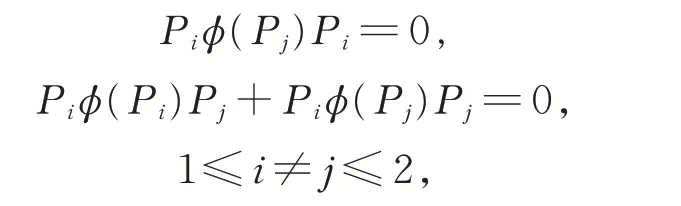
在式(1)中，令X =Y =Pi，Z=Xij∈Gij，则有

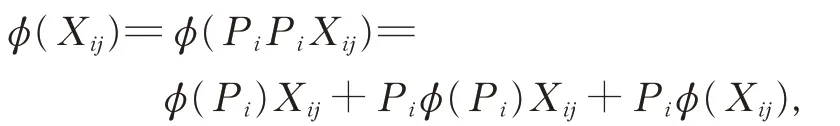
可得从而由Gij（1≤i ≠j ≤2）的忠实性,有

证毕。

注1令X0=P1φ(P1)P2-P2φ(P1)P1，对任意的X ∈G，定义映射δ:G ↦G 为

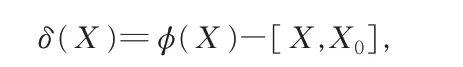
则δ 也是一个局部非线性三重可导映射，即对任意的X,Y,Z ∈G 且XYZ ∈Ω, 有

且由引理1 容易验证δ(P1)=δ(P2)=0。

引 理2对 任 意 的Xij∈Gij（1≤i,j ≤2）,有δ(Xij)∈Gij。

证明对任意的Xii∈Gii，一方面在式(2)中，令X =Xii， Y =Z=Pj（1≤i ≠j ≤2） ， 由 于δ(Pj)=0，从而有δ(Xii)Pj=0，进而有

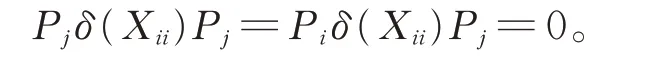
另一方面在式(2)中，令X =Pj,Y =Xii,Z=Pi（1≤i ≠j ≤2），可得Pjδ(Xii)Pi=0,从而δ(Xii)∈Gii。

对任意的Xij∈Gij（1≤i ≠j ≤2），在式(2)中，令X =Pi,Y =Xij，Z=Pj，可得

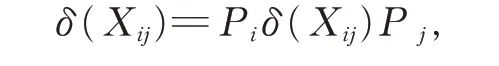
从而δ(Xij)∈Gij。

证毕。

引 理3对 任 意 的Xii∈Gii,Xjj∈Gjj,Xij∈Gij（1≤i ≠j ≤2）,有

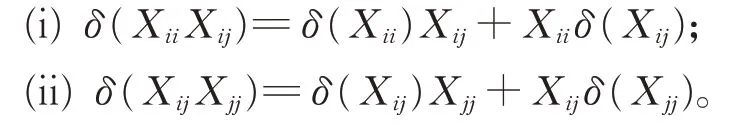
证 明（i）对 任 意 的Xii∈Gii, Xij∈Gij（1≤i ≠j ≤2）,在 式(2)中，令X =Xii,Y =Xij,Z=Pj，由引理2，有

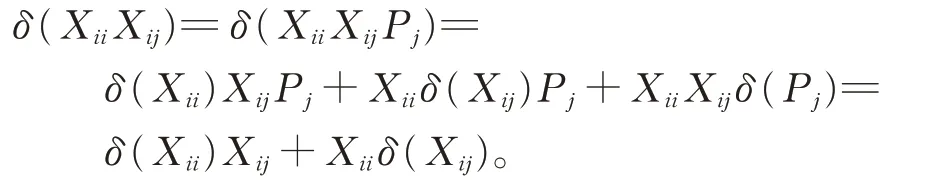
类似地，可以证明（ii）亦成立。

证毕。

引 理4对 任 意 的Xii∈Gii,Xij∈Gij,Xji∈Gji（1≤i ≠j ≤2）,有

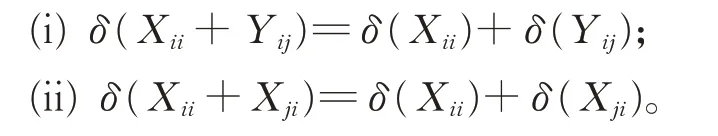
证明（i）对任意的Xii∈Gii,Xij∈Gij,Xji∈Gji（1≤i ≠j ≤2）,在式(2)中，令

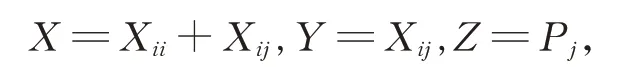
由引理2，有

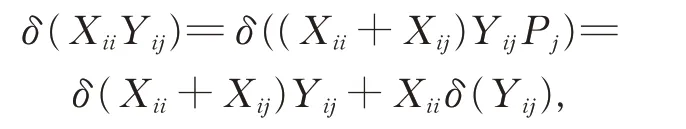
从而由引理3(i)，可得

进而由Gij（1≤i ≠j ≤2）的忠实性，有

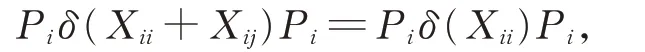
在 式(2)中，令X =Pi，Y =Xii+Xij，Z=Pj（1≤i ≠j ≤2），有

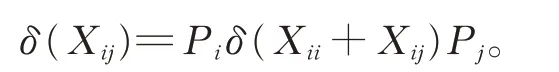
在式(2)中，令X =Xii+Xij，Y =Z=Pj（1≤i ≠j ≤2），有

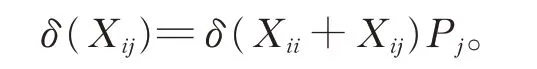
从而由引理2，有

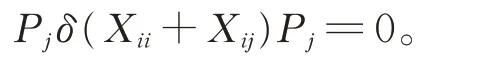
类似地，可以证明Pjδ(Xii+Xij)Pi=0。所以有

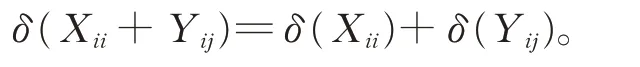
类似地，可以证明（ii）亦成立。

证毕。

引理5对任意的Xii,Yii∈Gii,Xij,Yij∈Gij（1≤i ≠j ≤2）,有

证明(i)对任意的Xij,Yij∈Gij（1≤i ≠j ≤2）,在式(2)中，令X =Pi+Xij,Y =Pj+Yij,Z=Pj,由引理2 和引理4，有

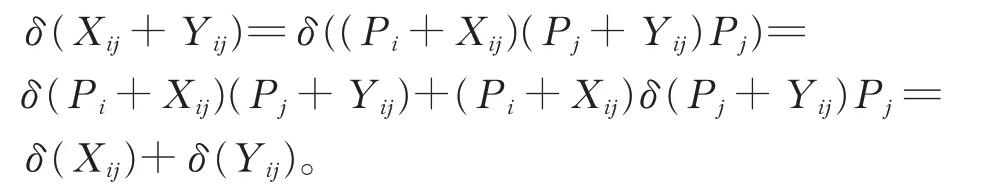
（ii）对 任 意 的 Xii,Yii∈Gii和 Cij∈Gij（1≤i ≠j ≤2）,在 式(2)中，令X =Xii+Yii,Y =Cij,Z=Pj,有

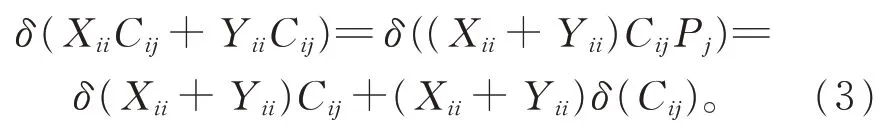
又由引理3(i)和引理5(i)，有

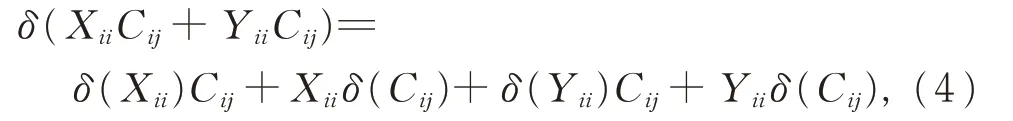
比较式(3)和式(4)，得

进而由Gij（1≤i ≠j ≤2）的忠实性及引理2，有

证毕。

引理6对任意的Xij∈Gij（1≤i,j ≤2）,有

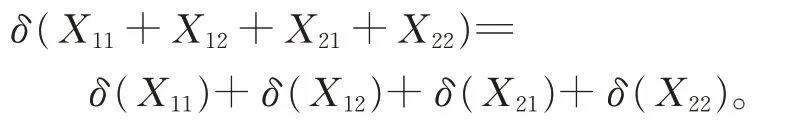
证明对任意的Xij∈Gij(1≤i,j ≤2）,在式（2）中 ， 令 Y =X11+X12+X21+X22, X =P1,Z=P2,有

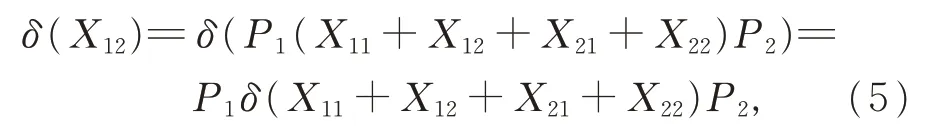
在式（2）中，令Y =X11+X12+X21+X22,X =P2,Z=P1,有

对任意的C12∈G12,在式（2）中，令Y =X11+X12+X21+X22,X =P1,Z=C12,由引理2，有

另一方面，由引理3，有

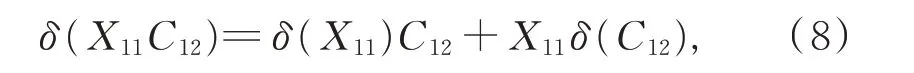
比较式（7）和式（8），得到

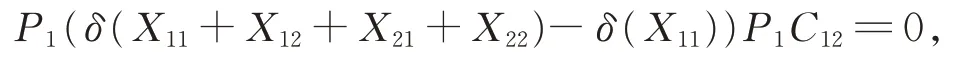
进而由G12的忠实性及引理2，有

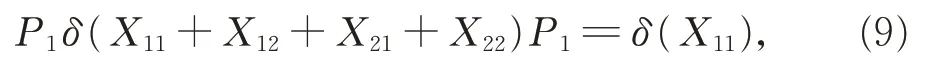
类似地，可以得到

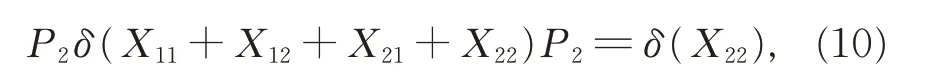
从而由式(5)、(6)、(9)、(10)，有

证毕。

引 理 7对 任 意 的 Xii,Yii∈Gii, Xij∈Gij,Xji∈Gji（1≤i ≠j ≤2）,有

证 明(i)对 任 意 的Xii,Yii∈Gii,Cij∈Gij（1≤i ≠j ≤2）,由引理3，一方面有

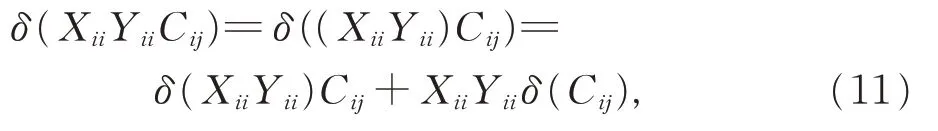
另一方面，有

比较式(11)和式(12)，得

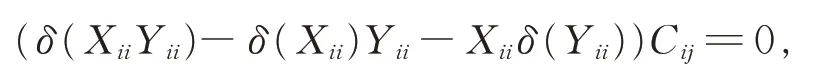
进而由Gij（1≤i ≠j ≤2）的忠实性及引理2，有

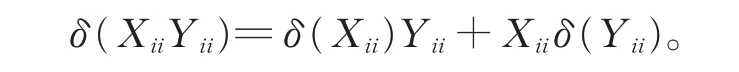
（ii）对 任 意 的Xij∈Gij,Xji∈Gji（i ≠j）,由 于(Xij-XijYji)(Yji+Pi)Pi=0，在 式(2)中,令X =Xij-XijYji,Y =Yji+Pi,Z=Pi，从而由引理2 和引理6，有

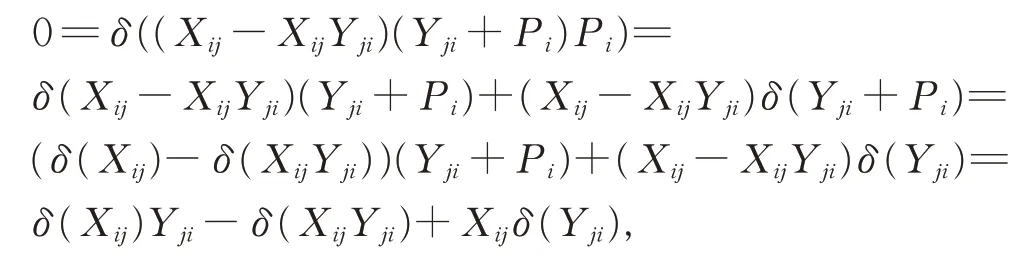
从而有

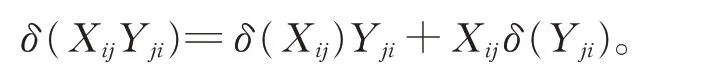
证毕。

定理1 的证明对任意的X,Y,Z ∈G，设

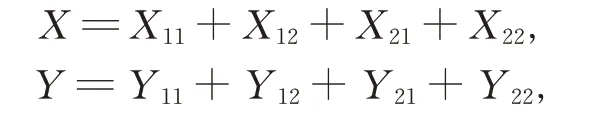
其中，Xij,Yij∈Gij，1≤i,j ≤2，由引理5 和引理6，有

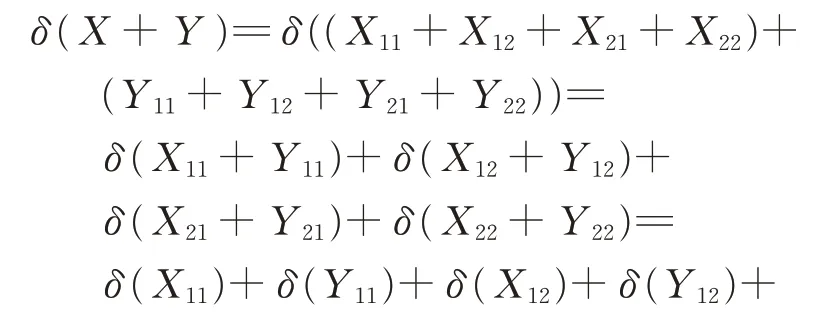
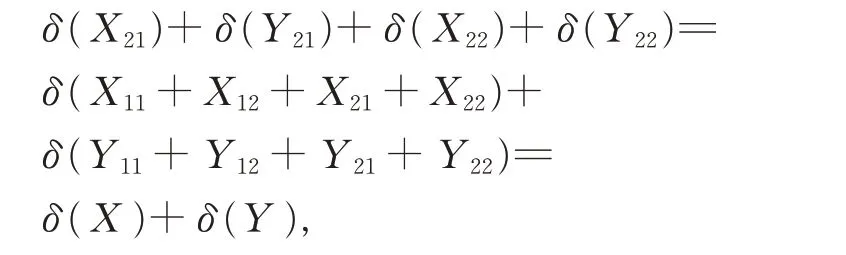
即δ 是G 上的一个可加映射, 从而由δ 的定义知，φ是G 上的一个可加映射。又由引理2、引理3 和引理7, 有

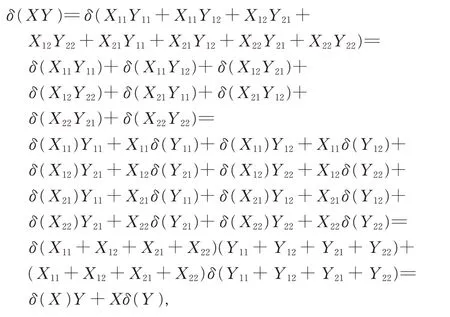
即δ 是一个导子, 所以φ 是广义矩阵代数G 上的一个导子。

证毕。

作为定理的应用, 有以下推论。

设Α 和Β 是含有单位元的交换环R 上的代数,若Μ 是忠实(Α,Β)-双边模，即Μ 既是忠实左Α 模又是忠实右Β 模, 则称R-代数

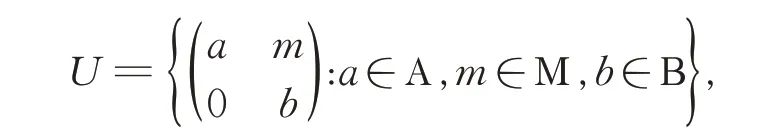
在矩阵通常的加法与乘法运算中是一个三角代数。

推论1设U 是一个2-无挠素三角代数，Ω={T ∈U:T2=0}，且φ 是U 上的一个映射(无可加性假设), 若对任意的X,Y,Z ∈U 且XYZ ∈Ω,有

φ(XYZ )=φ(X )YZ+Xφ(Y )Z+XYφ(Z )，则φ 是一个导子。

推论2设R 是一个有单位元I 且存在非平凡幂等元P 的2-无挠素环，Ω={r ∈R:r2=0}且φ 是R 上的一个映射(无可加性假设), 若对任意的x,y,z ∈R 且xyz ∈Ω, 有

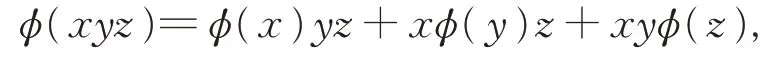
则φ 是一个导子。

证明设Q=I-P，则由于R 是素的，从而PRQ 是忠实的(PRP,PRQ)-双边模，所以R 同构于广义矩阵代数环：

因此，由定理1 知，φ 是一个导子。

设Χ 是数域C 上的Banach 空间,B(Χ)是Χ 上的全体有界线性算子,A(Χ)是B(Χ) 的一个子代数,F(Χ)是B(Χ)中包含全体有限秩算子的一个理想。若F(Χ)⊆A(X ),则称A(Χ)是一个标准算子代数。

设Η 是数域C 上的Hilbert 空间,B(Η)是Η 上的全体有界线性算子,V 是作用在Η 上的一个von Neumann 代数，I 是B(Η)里面的单位算子,Ζ 是V的中心，V′={T ∈B(Η):TB=BT,∀B ∈V}是V 的一次换位。若Z=V′∩V=CI, 则称V 是一个因子von Neumann 代数。

由于标准算子代数和因子von Neumann 代数都是存在非平凡幂等元的素代数，因此，由推论2 ，有

推论3设Χ 是数域C 上的Banach 空间, A(Χ)是Χ 上有单位元的标准算子代数,Ω={T ∈A(Χ):T2=0}，且φ 是A(Χ)上的一个映射(无可加性假设), 若 对 任 意 的 算 子 A,B,C ∈A(Χ) 且ABC ∈Ω, 有

则φ 是一个导子。

推 论4设Η 是 数 域C 上 的Hilbert 空 间, V 是作用在Η 上的一个因子von Neumann 代数，Ω={T ∈V:T2=0}，且φ 是V 上的一个映射(无可加性假设), 若对任意的算子A,B,C ∈V 且ABC ∈Ω, 有

φ(ABC)=φ(A)BC+Aφ(B)C+ABφ(C),则φ 是一个导子。