具正负系数和多变时滞的高阶微分方程的振动性

覃桂茳，刘玉周，杨甲山

（1.梧州学院大数据与软件工程学院，广西梧州543002； 2.梧州学院广西高校行业软件技术重点实验室，广西梧州543002； 3.梧州学院机械与材料工程学院，广西 梧州543002； 4.梧州学院广西高校图像处理与智能信息系统重点实验室，广西梧州543002）

0 引 言

在微分方程理论中，振动性是其重要的分支之一，并广泛应用于物理力学、控制系统、时间延迟系统、电力系统、时变非线性反馈系统等。微分方程的振动性广受关注且成果颇丰[1-14]。但具有正负系数和多变时滞的高阶方程振动性的研究成果却很少。考虑以下微分方程

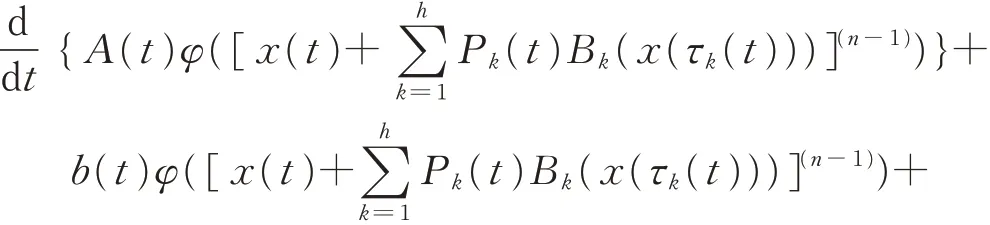
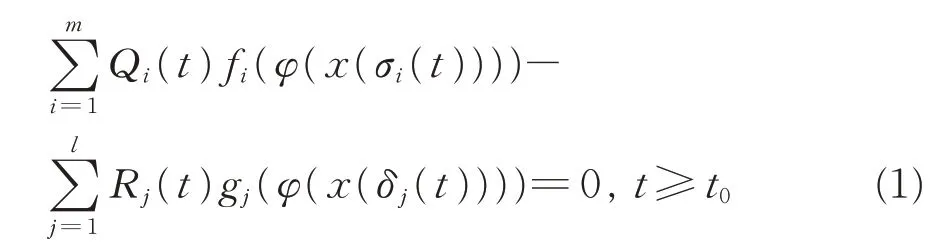
的 振 动 性，其 中n ≥2 为 偶 数，t0≥0 为 实 常 数；φ(u)=|u|γ-1u,γ ＞0 为实常数；h ≥1，m ≥1，l ≥1，均为整数。全文总假设条件(H0)～(H5)成立：

(H0) 函 数 A(t)， Pk(t)， b(t)， Qi(t)，Rj(t)∈C([t0,+∞),[0,+∞)),k=1,2,…,h；i=1,2,…,m； j=1,2,…,l( 下 同 , 略)； Bk(u)，fi(u),gj(u)∈C(R,R) 且 uBk(u)＞0(u ≠0)，ufi(u)＞0(u ≠0)，ugj(u)＞0(u ≠0)。

(H1) 函 数 τk(t)∈C([t0,+∞),(0,+∞))，

(H2) 函数σi(t)=δj(t)=σ(t)∈C1([t0,+∞),

(H3) 存在常数0 ＜ηk≤1,αi＞0,βj＞0，使得当 u ≠0 时 有 Bk(u)/u ≤ηk， fi(u)/u ≥αi，并 且最终成立。

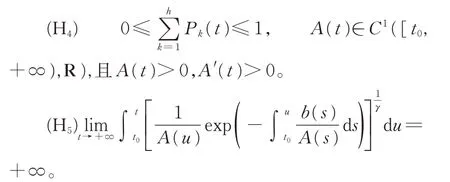
关于方程(1)的解及其振动性的定义参见文献[1-12]，本文只讨论方程(1)的非平凡解。方程(1)包括了许多典型的微分方程，如二阶Emden-Fowler型方程：

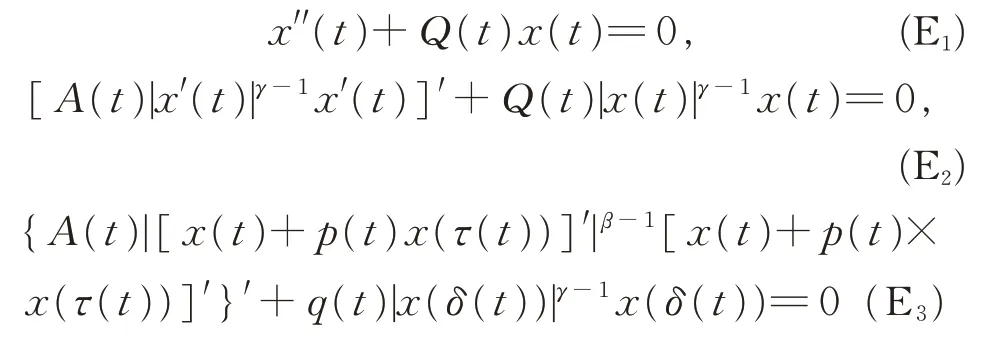
及具有正负系数的二阶方程：

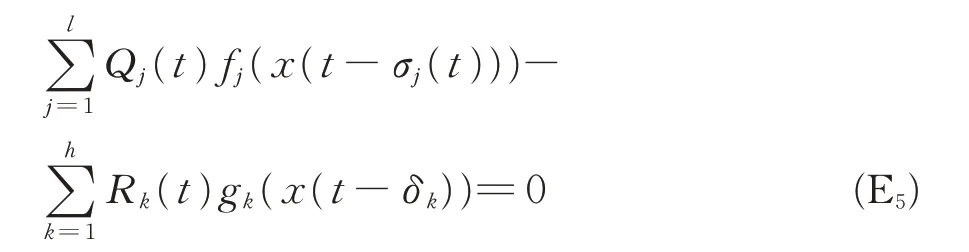
等。这些典型的微分方程已有许多很好的振动准则[1-12]。如KAMENEV[1]改 进 了WINTNER 的 结果，得到了以下振动准则(称之为Kamenev 型振动准则)：

定理A[1]若+∞（μ ＞1 为常数），则方程(E1)振动。

之后，LI 等[2]将KAMENEV 的结果推广到了二阶半线性微分方程(E2)，得到

定理B[2]若如 存在常数k ＞γ，使得

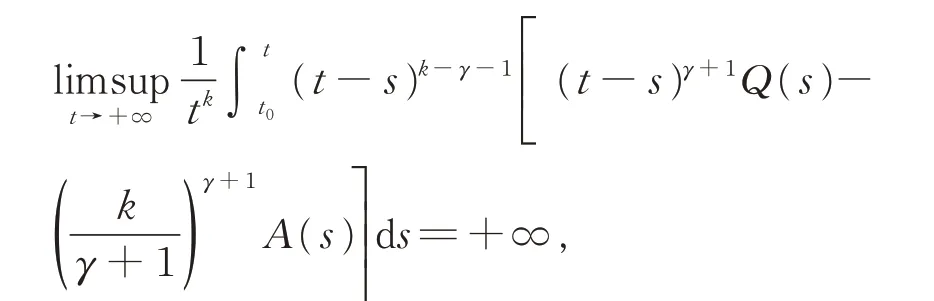
则方程(E2)振动。

以此为基础,黄记洲等[3]研究了更一般的二阶Emden-Fowler 型方程(E3)，并得到方程(E3)振动的一系列新准则，其Hille 型振动准则如下：

定 理C[3]设β ≥γ，A′(t)≥0，δ′(t)＞0，0 ≤p(t)＜1，且若 存 在 函 数φ ∈C1([t0,+∞),(0,+∞))，使得

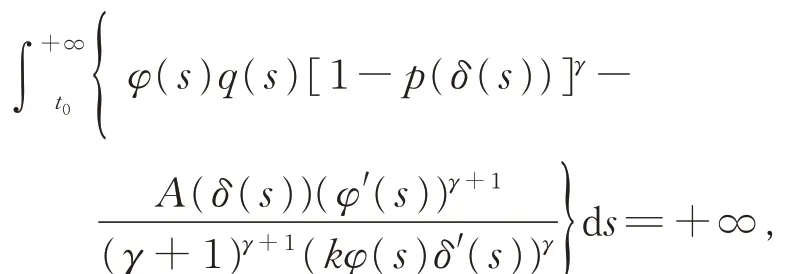
其中k ＞0 为常数，则方程(E3)振动。

对具有正负系数的二阶微分方程，仉志余等[4]率先研究了方程(E4)的振动性，结果如下：

定理D[4]设0 ≤P(t)＜1，Q(t)≥0 且R(t)最终为负，若

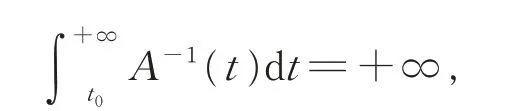
紧接着，杨甲山等[5]研究了一类广泛的具有正负系数的二阶方程(E5)的振动性，放宽了文献[4]的条件，得到了方程(E5)的振动准则(包括Hille 型准则和Kamenev 型准则等)。其他结果可参见文献[6-10]，而对具有正负系数及多时滞的高阶微分方程的振动性研究成果目前还很少。

本文的目的是研究具有正负系数和多变时滞的高阶阻尼微分方程(1)的振动性，进一步改进并拓展现有的研究成果，使得定理A～定理D 成为本文结果的特例，最后用一些具体实例说明本文的主要结论。

1 引 理

引入记号

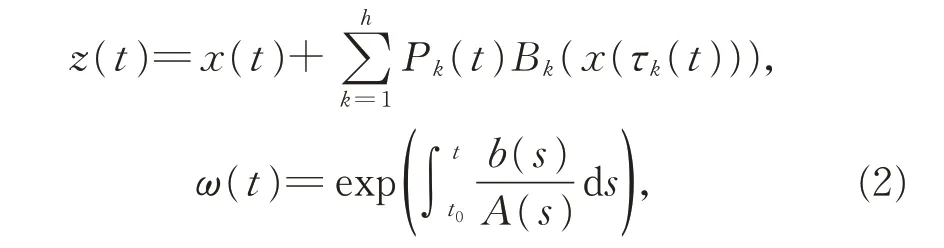
则方程(1)可写为

引理1[7]设u(t)在[t0,+∞)上是正的n 次可微函数，u(n)(t)最终定号，则存在t*≥t0和整数l(0 ≤l ≤n)，当u(n)(t)≥0 时，n+l 为 偶 数；当u(n)(t)≤0 时，n+l 为 奇 数，使 得 当l ＞0 时，有u(k)(t)＞0，t ≥t*，k=0,1,…,l-1；且 当l ≤n-1时 ， 有 t ≥t*； (-1)l+ku(k)(t)＞0； k=l,l+1,…,n-1。

引理2[7]设u(t) 满足引理1 的条件，且u(n-1)(t)u(n)(t)≤0(t ≥t*)，则对任意θ ∈(0,1)，存在常 数M ＞0，使 得 对 一 切 充 分 大 的t 有u′(θ t)≥Mtn-2u(n-1)(t)。

引理3[7]设a，b 为非负实数，则aλ-λabλ-1+(λ-1)bλ≥0，λ＞1，等号成立当且仅当a=b。

引理4设x(t)是方程(1)的最终正解，则

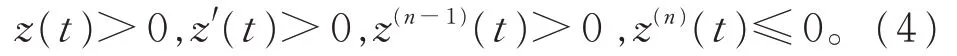
证明因为x(t)是方程(1)的最终正解，不妨设当t ≥T ≥t0时，x(t)＞0，x(τk(t))＞0，x(σi(t))=x(δj(t))=x(σ(t))＞0，于是

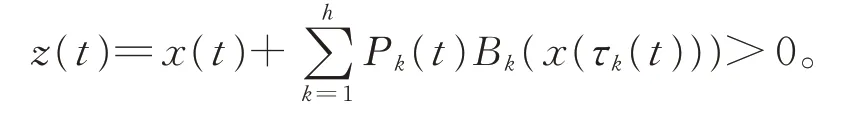
由方程(3)并注意到条件(H3)，得

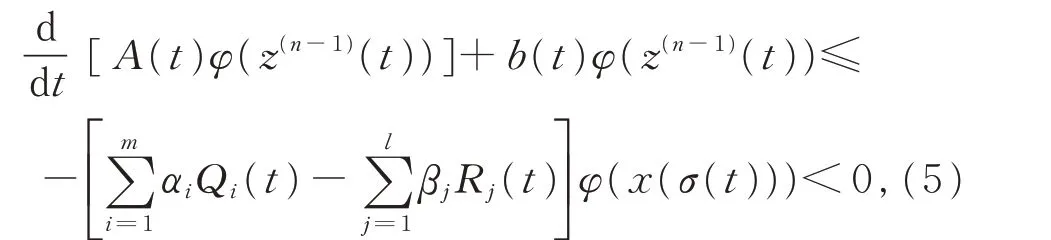
因此ω(t)A(t)φ(z(n-1)(t))是减函数，并且z(n-1)(t)最终定号，且能断言：

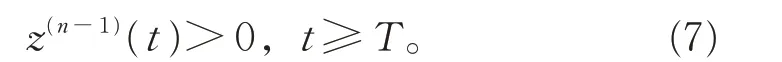
事实上，若z(n-1)(t)＜0，t ≥T。由式(6)，得

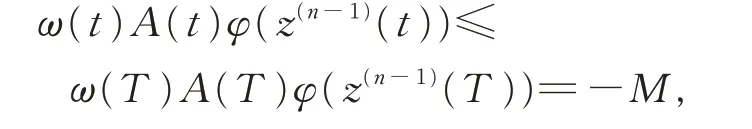
其中常数

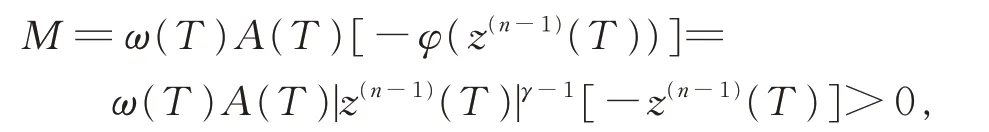
于是由上式得

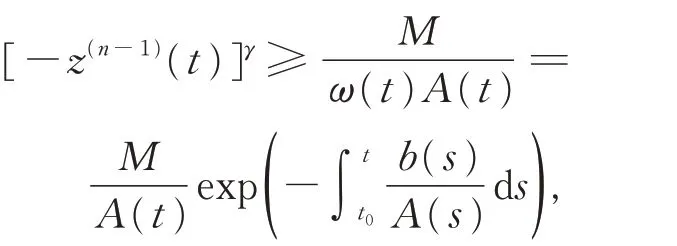
进一步，有

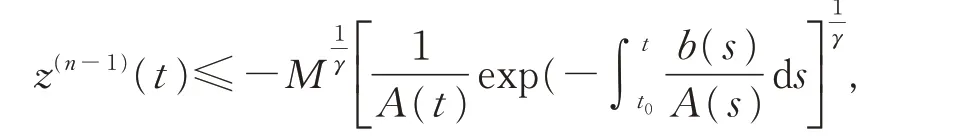
于是有

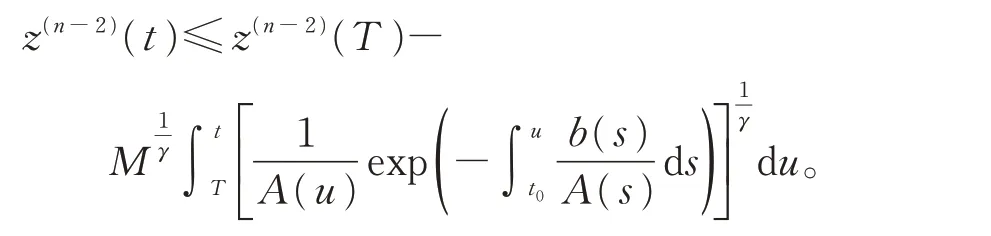
在 上 式 中 ，令 t →+∞，注 意 到 (H5)，得类 似 可 得这 与z(t)＞0 矛盾！故式(7)成立。

由式(5)知，

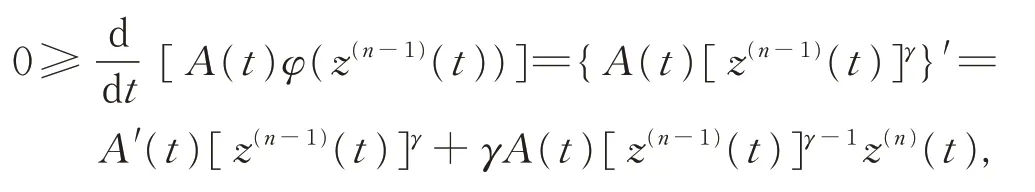
由此推得z(n)(t)≤0(t ≥T)。因为n 是偶数，于是由引理1 中l 为奇数，有z′(t)＞0(t ≥T)。 证毕。

2 方程（1）的振动准则

定 理 1如 果 存 在 函 数 ρ(t)∈C1([t0,+∞),(0,+∞))，使得

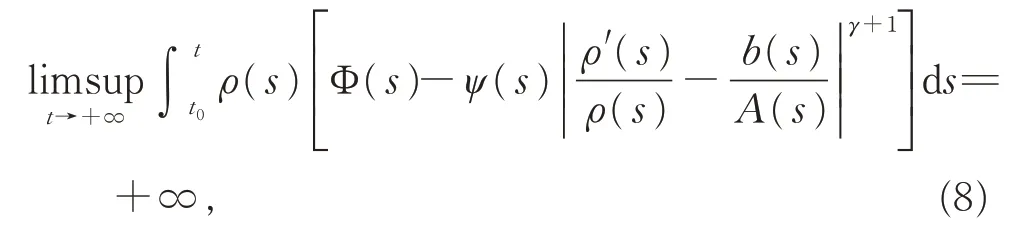
其中函数Φ(t)和ψ(t)的定义如下：

常数θ ∈(0,1)和M ＞0 同引理2，则方程(1)振动。

证明设方程(1)存在非振动解x(t)，不失一般性，设x(t)＞0,x(τk(t))＞0，x(σ(t))＞0，t ≥T ≥t0。由引理4 知，式(4)成立。于是由引理2，对任意0 ＜θ ＜1，存在常数M ＞0，有

由式(2)的第1 个式子知，x(t)≤z(t)，于是

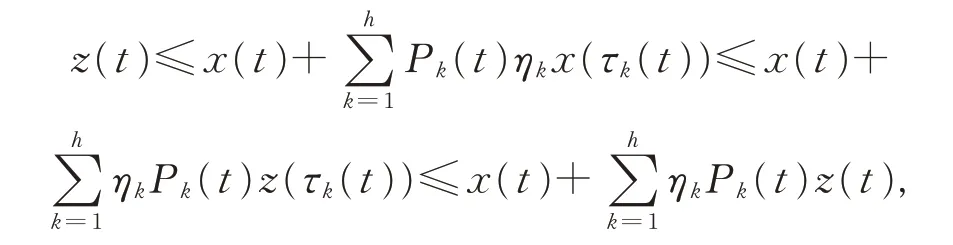
整理得

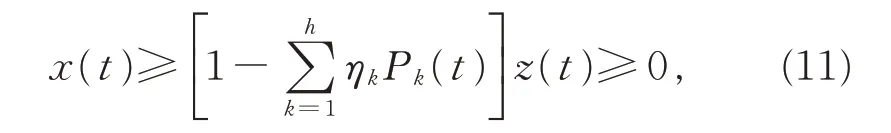
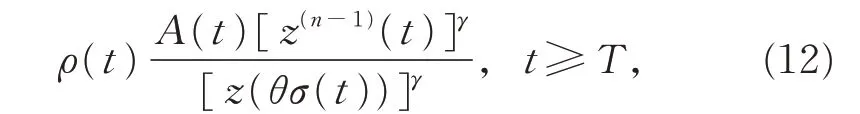
则V(t)＞0(t ≥T)，注意到式(5)、(10)和(11)，由式(12)可导出

注意到式(9)的第1 个式子，当t ≥T 时，由上式进一步可得

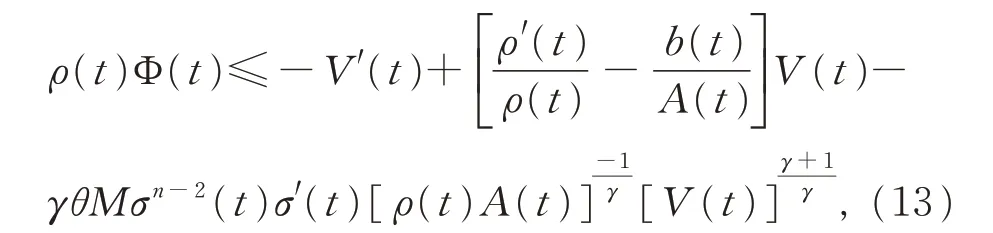
现取

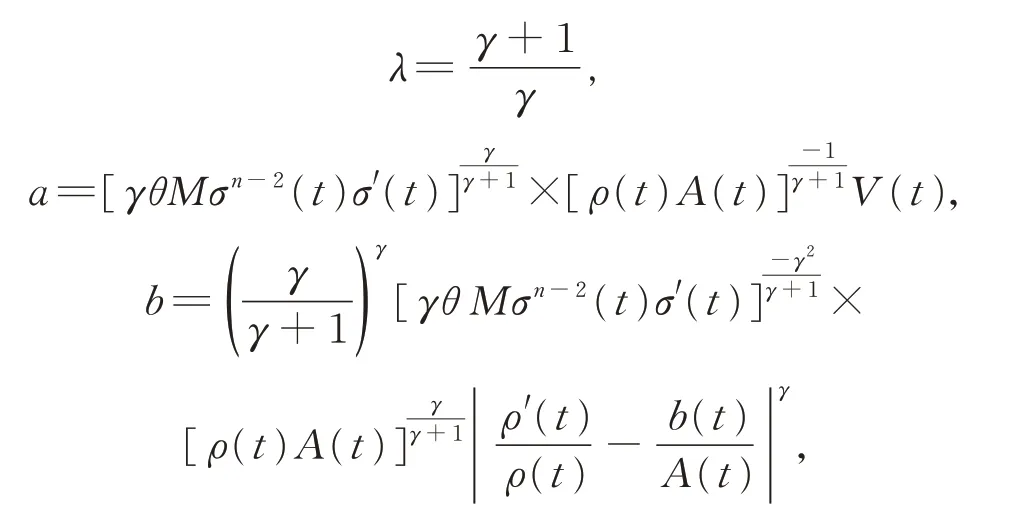
由引理3，有λabλ-1-aλ≤(λ-1)bλ，即

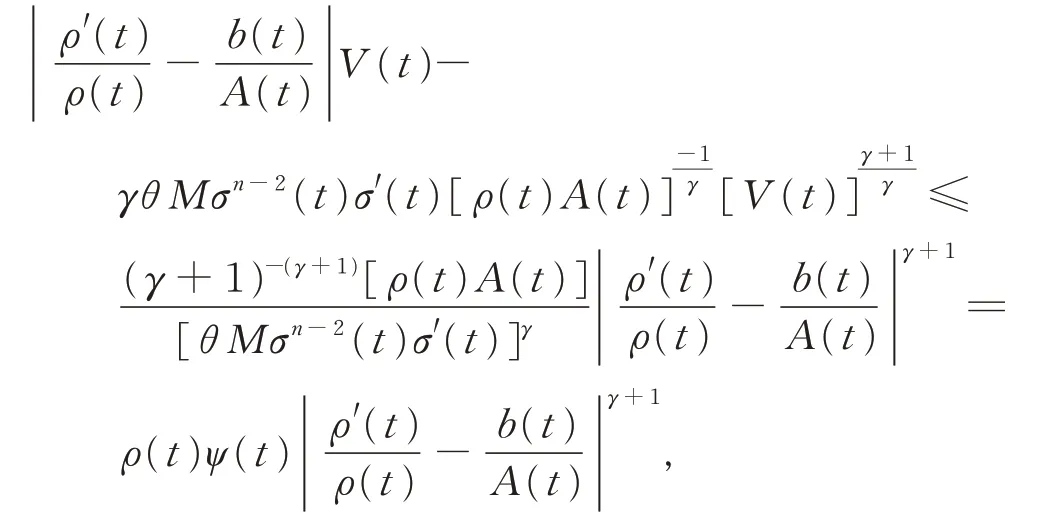
将上式代入式(13)，得

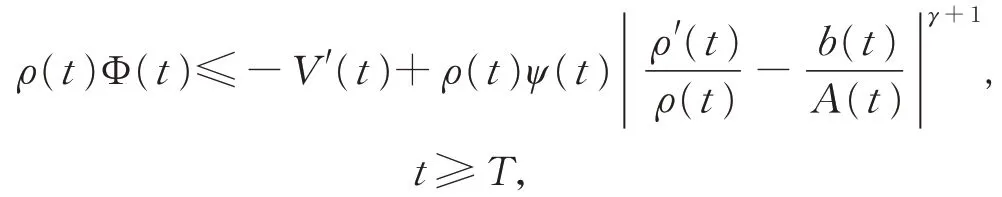
上式两边从T 到t 积分，可得

取上极限，则得到与式(8)矛盾的结果。定理1 证毕。

定 理 2如 果 存 在 函 数 ρ(t)∈C1([t0,+∞),(0,+∞))及常数μ ＞γ，使得

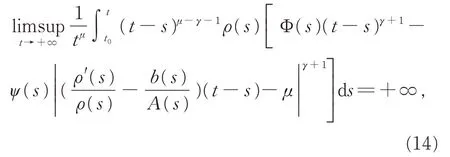
其中常数θ ∈(0,1)和M ＞0 的定义同引理2，而函数Φ(s)，ψ(s)的定义同式(9)，则方程(1)振动。

证明若不然，则方程(1)存在非振动解x(t)，不 失 一 般 性 ， 设 x(t)＞0,x(τk(t))＞0，x(σ(t))＞0，t ≥T ≥t0。由 引 理4 知，式(4)成 立。定义函数V(t)如式(12)，则由定理1 的证明知，式(13)成立，即当s ≥T 时，有

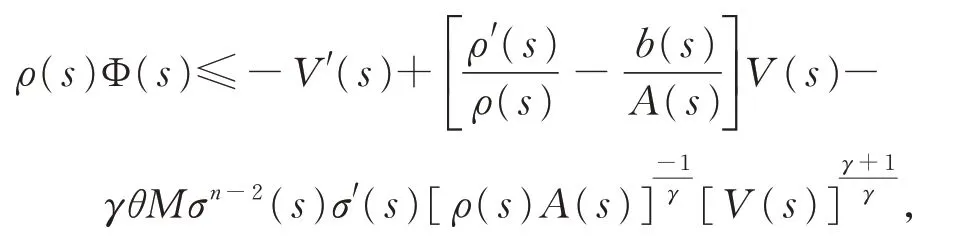
上式两边同乘以(t-s)μ，并从T 到t 积分，由分部积分法，整理得

现取

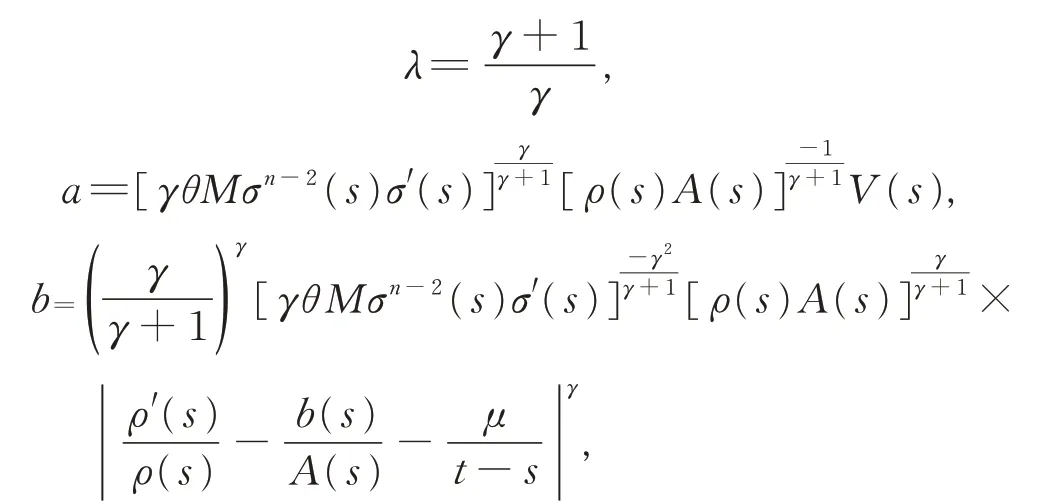
由引理3，有λabλ-1-aλ≤(λ-1)bλ，注意到式(9)的第2 个式子，可得

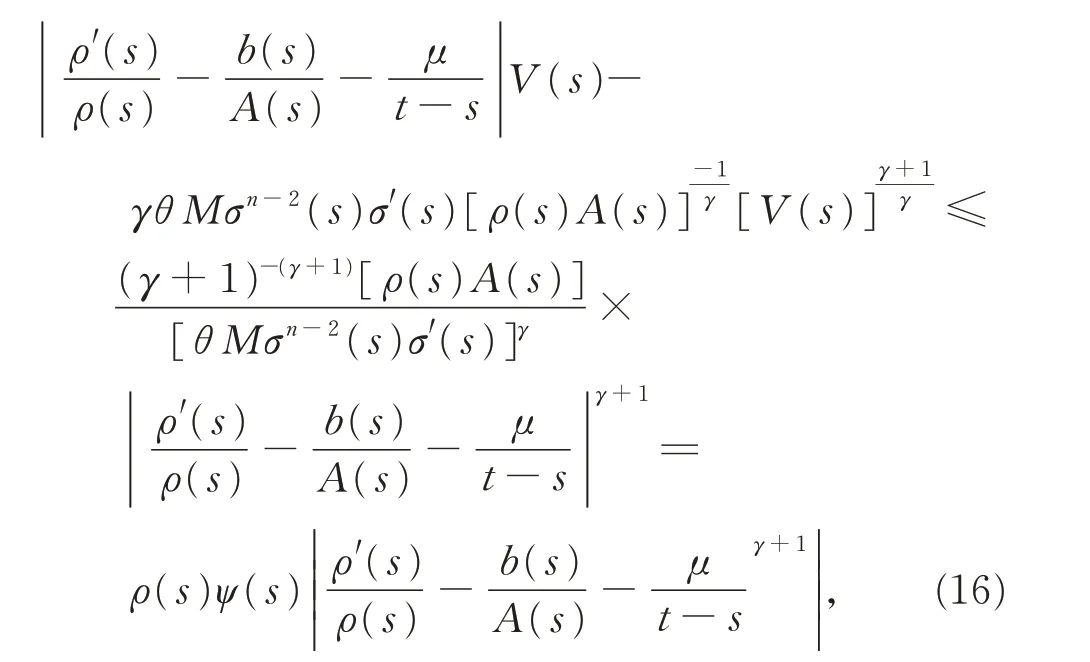
综合式(15)、(16)，有

即

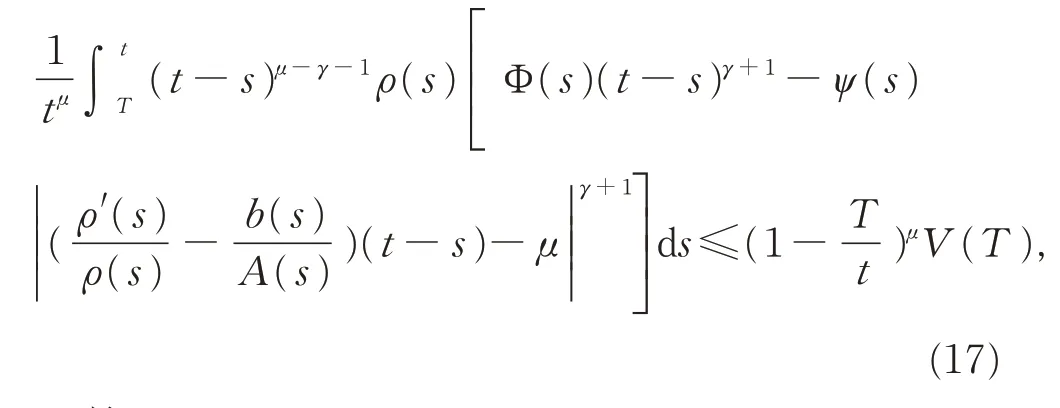
于是

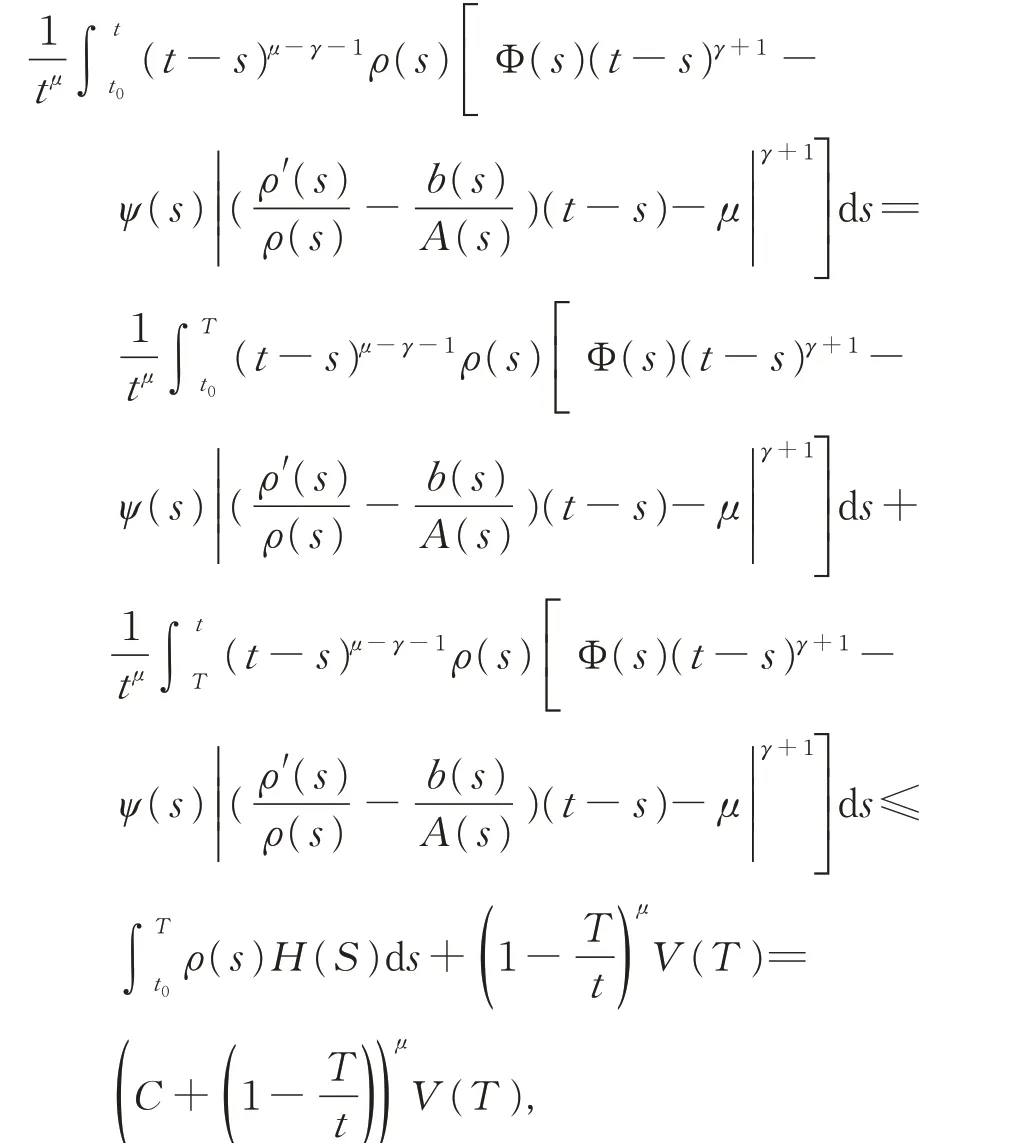
注 1若 方 程(1) 中 n=2，m=1，Pk(t)≡0，b(t)=0，Rj(t)≡0，f (u)=u，σ(t)=t，并在定理2 中取ρ(t)=1，于是由定理2，可得定理B。即定理A 和定理B 为定理2 的特例。此外，若方程(1)中，m=1，Pk(t)≡0，Rj(t)≡0，fi(u)=u，则定理1 即为文献[11]中的定理2；进一步，在定理2 中，取ρ(t)≡1，即得到文献[11]中的定理1。关于方程(1)的特殊情形的不同振动准则，可参考文献[5-11]。

注2若 方 程(1)中，n=2，h=m=l=1，b(t)≡0，γ=1，B(u)=u，τ(t)=t-τ0，σ(t)=t-σ0，δ(t)=t-δ0，则相应地，本文定理1 和定理2 即为具有正负系数的二阶微分方程(E4)的振动准则，但本文没有文献[4]的条件:“R(t)最终为负”，因此本文结果进一步改进并拓展了现有的研究成果。

例1考虑以下4 阶具有正负系数的变时滞方程

其中f,g 分别为f (u)=u[6+lnγ(1+u2)]，g(u)=这相当于方程(1)中

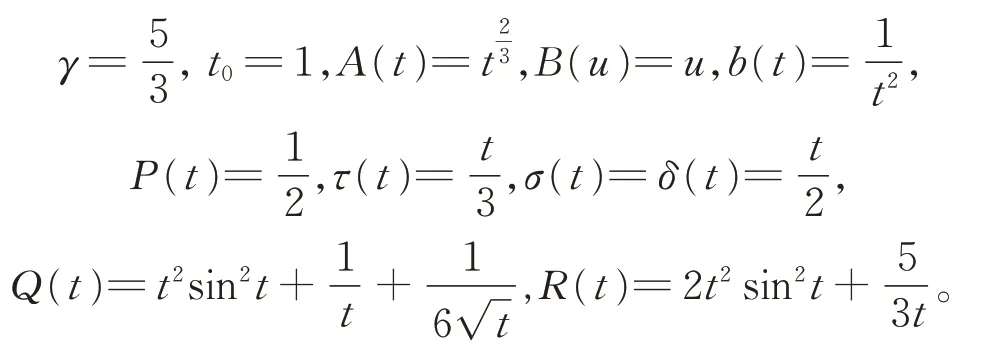
显然有

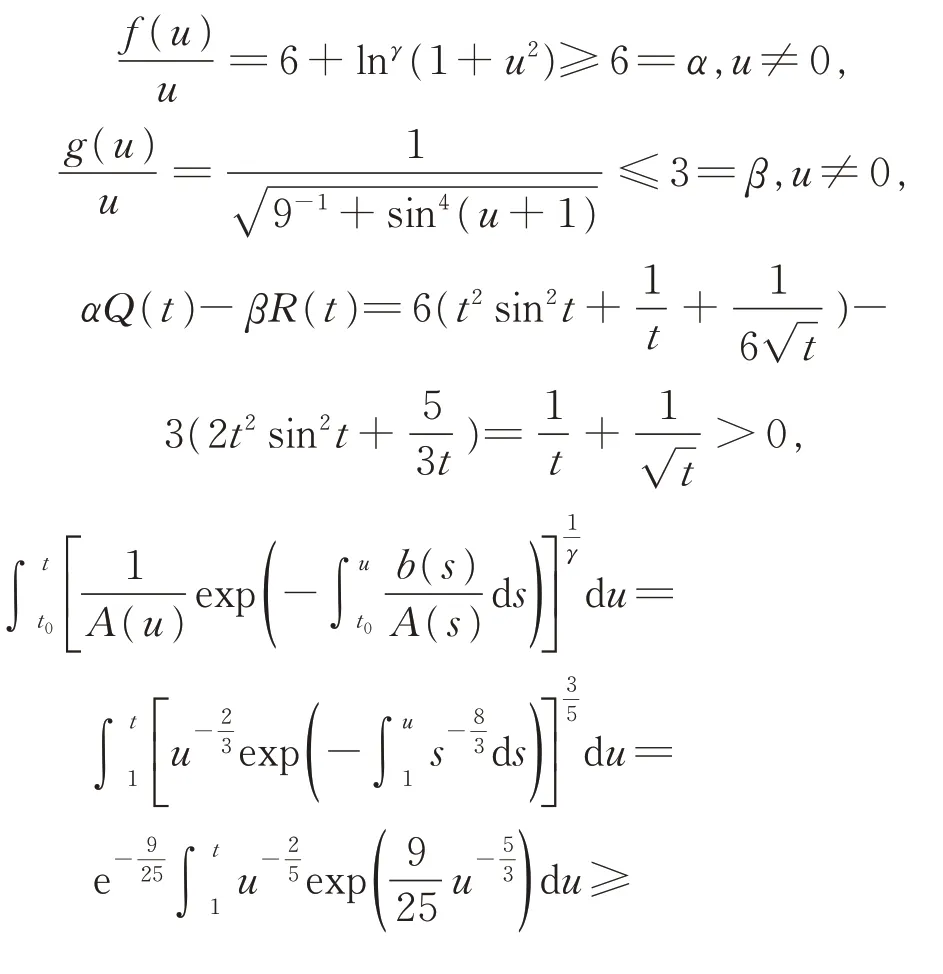
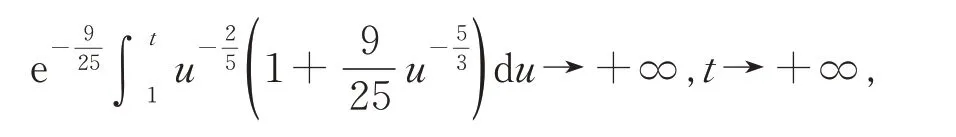
即条件(H0) ～(H5)成立。在定理1 中,取ρ(t)=1，并注意到式(9)，则有

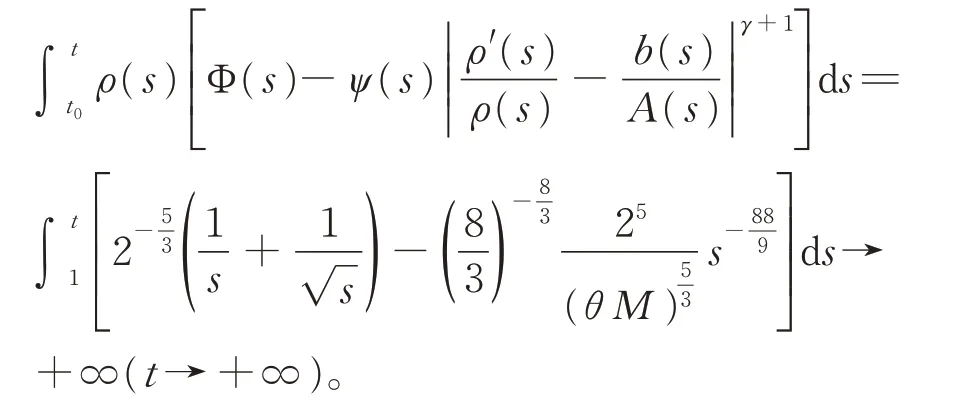
于是由定理1 知，方程(18)振动。

例2考虑具有正负系数和阻尼项的变时滞2阶方程

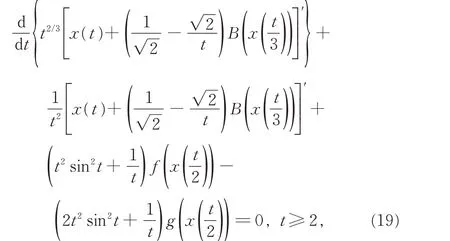
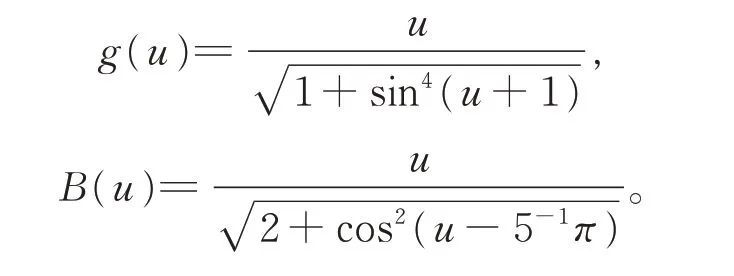
则

即 条 件(H0) ～ (H5) 成 立。 现 在 定 理2 中，取ρ(t)=1，μ=2 ＞γ，并注意到式(9)，则有

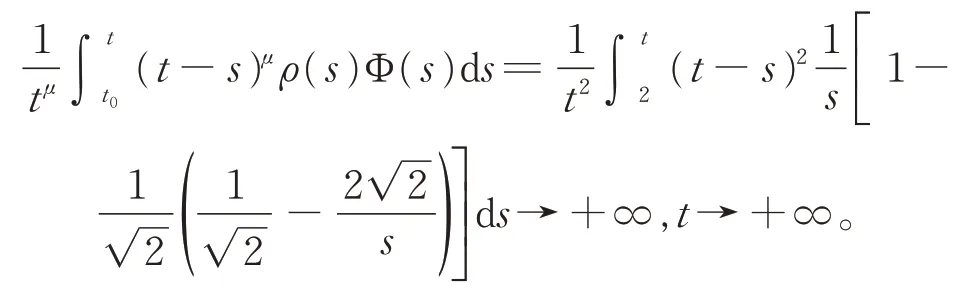
而

所以

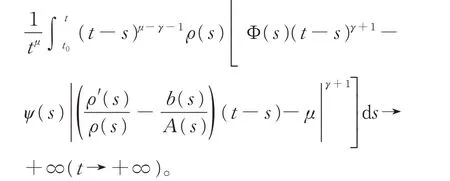
于是由定理2 知，方程(19)振动。显然文献[1-12]中的定理均不能用于方程(18)和(19)的振动性判别。