多圆柱上加权Bergman 空间到Bloch 型空间的加权Cesàro 算子

赵艳辉，廖春艳，邓春红，吴修云

(1.湖南科技学院理学院，湖南永州425199; 2.湖南科技学院理学院计算数学研究所，湖南永州425199)

0 引 言

表示Un上的加权Bergman 空间Αpα(Un)，其中

dv 表示Un上正规化的Lebesgue 体积测度，即v(Un)=1,dv(z)也可表示成

在单位球上, 文献[1-5]讨论了混合模空间、μ-Bloch 空间、Bloch 型空间和Dirichlet 型空间上的加权Cesàro 算子的有界性和紧性问题；文献[6-8]讨论了单位球Bergman 空间上的复合算子和Cesàro 算子的有界性和紧性问题。 记定 义Un上的加权Cesàro 算子Tg为

则Tg是线性算子。在多圆柱上, 文献[9-10]讨论了从Bergman 空间到Bloch 空间的加权复合算子的有界性和紧性的充要条件。文献[11]讨论了加权Bergman 空间上的复合算子的有界性和紧性问题。对于多圆柱上Bergman 空间上的加权Cesàro 算子的有界性和紧性问题尚未见结果。本文的主要工作是在Cn中的多圆柱上给出Tg为加权Bergman 空间到Bloch 型空间的有界算子和紧算子的充要条件。文 中 均 假 定 α=(α1,α2,…,αn),αj＞-1,j=1,2,…,n；c 表示与变量z,ω 均无关的正常数，不同地方可代表不同的值。

1 有关引理及证明

引理1[9]设，则

引 理2设0 ＜p,q ＜+∞,g ∈H(Un)，则Tg是Αpα(Un)到Βq(Un)上的紧算子的充要条件是:对Αpα(Un)中在Un上内闭一致收敛于0 的任意有界序列{ fm}，当m →∞时，有||Tg( fm)||Βq→0。

证明由引理1 和Montel 定理，按紧算子的定义便可证得。

2 主要结果及证明

定 理1设0 ＜p,q ＜+∞,g ∈H(Un)，则Tg是Αpα(Un)到Βq(Un)上的有界算子的充要条件是:

证明先证充分性。任取z ∈Un,f ∈Αpα，由引理1 及式(1)，有

又Tgf(0)=0, 所以Tg是有界的。

再证必要性。设Tg是Αpα(Un)到Βq(Un)的有界算 子，取 函 数

则

由文献[12]中的定理1.12, 有

所以hω∈Αpα, 且||hω||p,α=1。

由Tg的有界性，知

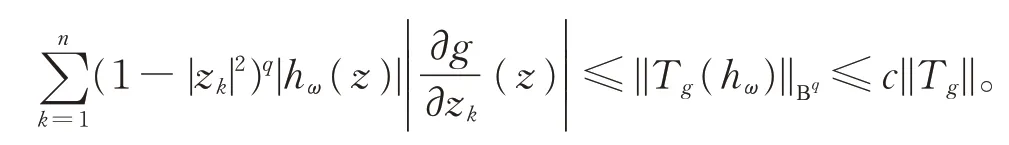
令z=ω,有

由ω 的任意性,知式(1)成立。定理1 得证。

对于单位圆盘的情形，不难得到以下结论：

推论1设0 ＜p,q ＜+∞,g ∈H(D)，则Tg是Αpα(D)到Βq(D)上的有界算子的充要条件是:

定 理2设0 ＜p,q ＜+∞,g ∈H(Un)，则Tg是Αpα(Un)到Βq(Un)上的紧算子的充要条件是:g ∈Βq(Un)，且

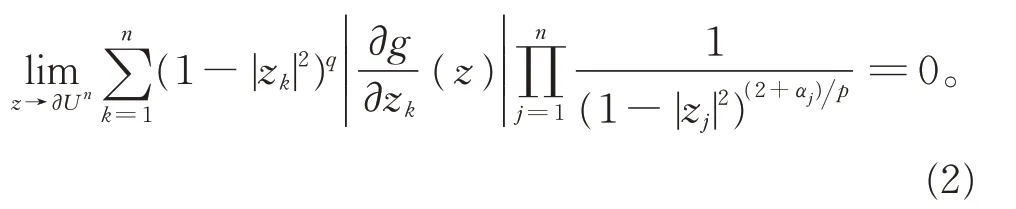
证明先证充分性。任取Αpα(Un)中一个在Un上内闭一致收敛于0 的有界序列{ fm}，不妨设||fm||Αpα(Un)≤1，由 式 (2)，∀ε ＞0,∃0 ＜δ ＜1, 当dist(z,∂Un)＞1-δ 时，有

(i) 当dist(z,∂Un)＞1-δ 时，由式(3)和引理1，有

(ii) 令 E={ z ∈Un:dist(z,∂Un)≤1-δ }, 则{ fm}在E 上一致收敛于0，当dist(z,∂Un)≤1-δ时，由g ∈Βq(Un)，有

由式(4)、(5),有

令m →∞，则||Tgfm||Βq≤ε，由ε 的 任 意 性，知||Tgfm||Βq→0。由引理2，知Tg为Αpα(Un)到Βq(Un)上的紧算子。

再证必要性。若Tg为Αpα(Un)到Βq(Un)上的紧算子，取f (z)=1∈Αpα(Un)，因为

所以g ∈Βq(Un)。

假设式(2)不成立，则存在ε0＞0 及Un中的点列{ zi}，当i →∞时，zi→∂Un，使得

又因为当i →∞时，zi→∂Un，因此，其分量中至少有一个模趋于1，即存在j0(1≤j0≤n)和{ zi}的子列，不 妨 设 为{ zi}，于 是 有zij0→1(i →∞)，即

下证{ fi}在Un上内闭一致收敛于0。

设E 为Un上任一紧子集，则存在0＜r＜1，使得则 由 式 (7)，知

所以{ fi}在Un上内闭一致收敛于0。由式(6)，有与引理2 矛盾，从而式(2)成立,定理2 得证。

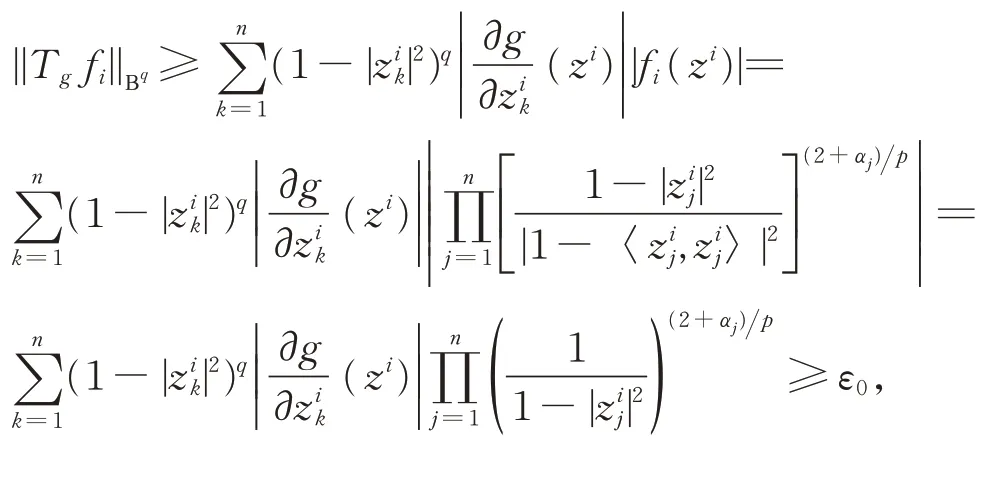
对于单位圆盘的情形，不难得到以下推论：

推论2设0 ＜p,q ＜+∞,g ∈H(D)，则Tg是Αpα(D) 到Βq(D) 上 的 紧 算 子 的 充 要 条 件 是:g ∈Βq(D)，且