《长方体的认识》教学实录与评析

邓星华 韦莉

教学《长方体的认识》这一内容时，教师应结合学习内容给学生创设一定的操作活动。那么，是否一定要有操作环节呢？能否通过推理或想象，让学生掌握长方体的特征？基于范希尔理论的五个思维水平的分析，五年级学生的几何思维水平处于分析阶段，已经具备丰富的视觉辨别经验，能够分析图形的组成要素，并且根据这些要素特征解决简单的几何问题，但是还无法清楚地解释图形性质之间的关系。因此，五年级学生认识长方体不需要动手操作也可以掌握其特征。本课教学借助多媒体信息技术，利用逻辑推理和想象的方式，引导学生认识长方体的特点。

一、从零维到三维，初步认识长方体

师：请同学们看大屏幕，你看到了什么？（动画演示点动成线、线动成面、面动成体的过程，以及长方体的形成过程）

生：图形最后变成了长方体。

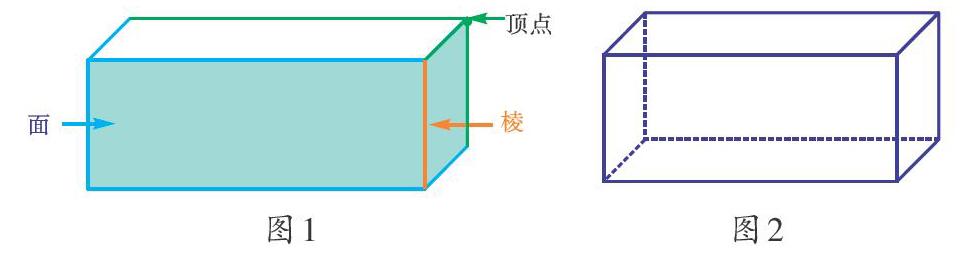
师：是的。动画演示的是点动成线、线动成面、面动成体的过程。今天，我们就来进一步认识长方体。仔细观察，长方体有面，面和面相交的线段是棱，棱和棱的交点是顶点。（课件动态呈现长方体各部分名称，如图1）

师：这个长方体和我们平时看到的长方体有什么不一样呢？（课件出示长方体的透视图，如图2）

生：图1有3条棱看不见，图2把它们用虚线都画出来了。

师：对。长方体的透视图可以帮助我们观察到长方体的每一个面和每一条棱。

【评析】研究图形要从三维到二维再到一维，最后到零维，将高维度的图形分解成低维度的元素。执教老师利用课件动态演示点动成线、线动成面、面动成体的过程，最后回到点、线、面、体，这样做有利于学生感知事物组成的各个元素，突出数学概念的本质属性。

二、想象推理，概括长方体的特征

（一）完成预学单，交流质疑

师：课前，同学们已经在平板电脑上完成预学单（见表1），下面我们一起来看大家做题的情况。（课件呈现学生完成预学单的情况，如图3）

师：我发现同学们对长方体的面、棱、顶点的数量及关系有不同的理解。到底谁的理解正确呢？

（二）利用“學习资源包”自主学习

师：请同学们先看学习要求。（课件出示学习要求：①分别数出长方体的面、棱、顶点的数量;②研究长方体面与面、棱与棱之间的关系;③修改预学单）

生在平板电脑上点击“学习资源包”自主学习，修正预学单。“学习资源包”的内容如下：

①3D动态几何软件：将长方体旋转—展开长方体的外衣—脱掉长方体的外衣—剩下长方体的棱（如图4）。

②视频：推动长方体相对的面重合，推动长方体相对的棱重合（如图5）。

（三）交流反馈，思维碰撞

1.研究长方体的棱

师：谁来说一说，你在预学单上做了哪些修改？

生1：我原本认为长方体有8条棱，数过之后发现，它有12条棱。

师：请你用手比划一下，这12条棱分别在哪里？

生1：（在长方体的透视图上比划）我将2条棱作为一组来数。

生2：（在长方体的透视图上比划）我将4条棱作为一组来数。

师：两位同学有序地数出了长方体的12条棱。对比两位同学的方法，你更喜欢哪一种？

生：我喜欢将4条棱作为一组来数，因为这样更清晰。

师：也就是说，它能让我们更清楚地看到这3组棱的方向是一样的，对吗？很好，我们再来看棱的关系。有的同学写“上下棱长度相等，左右棱长度相等”，有的同学写“长的棱长度相等，短的棱长度相等”，有的同学写“相对的棱长度相等”。你和谁英雄所见略同？或者你跟谁的看法不同？

生：我认为“上下方向的棱长度相等”，这4条棱方向相同，也就是相对的棱长度相等，左右方向跟前后方向也一样。

师：大家听明白了吗？在长方体中，这条棱和这条棱是相对的，这两条棱也是相对的，这4条棱其实都是相对的。（课件演示推动长方体相对的棱重合，如图5）

生：通过推动长方体相对的棱重合，我们发现，“相对的棱长度相等”。

师：我们把相对的棱重合，像这样相交于一个顶点的三条棱，就叫做长方体的长、宽、高。（课件演示三条棱重合，得出长方体的长、宽、高）

2.研究长方体的面

师：刚才我们研究了长方体的棱，接下来观察长方体的面。长方体有6个面，你们同意吗？

生：同意！

师：这6个面分别在哪里呢？

生上台指着长方体的透视图，数出长方体的6个面。（课件呈现学生数的顺序以及相应的面）

师：有不同的数法吗？

生上台展示不同的数法。

师：你们发现了吗？只要有序地数，就能准确地数出长方体的6个面。关于面的关系也有不同的写法，你能看懂吗？

生1：长方体的上面和下面完全相同，前面和后面完全相同，左面和右面完全相同。

生2：上面和下面、前面和后面、左面和右面是相对的面，即相对的面完全相同。

师：（课件动态演示长方体的面的重合）将面与面重合，我们就能发现长方体相对的两个面完全相同。

3.研究长方体的顶点

师：还有长方体的顶点呢？是哪8个顶点？

生结合长方体的透视图数出长方体顶点的数量，师根据学生的回答，完成板书（见表2）。[长方体 面 棱 顶点 数量 6 12 8 关系 相对的面完全相同 相对的棱长度相等 ]

【评析】自主学习能力是人类生存的基本能力。执教老师借助信息技术软件，通过组合学习资源包，让学生在平板电脑上自主学习，同时利用3D动态几何软件立体展现长方体的棱，有助于学生掌握长方体的特征。

（四）研究各要素之间的联系

师：我们从点、线、面3个角度研究了长方体的特征。现在，让我们回到开课时看到的长方体，这个长方体的长、宽、高分别是多少？

生：长是20厘米、宽是8厘米、高是10厘米。

师：仔细看，长方体要发生变化了，你发现什么改变了？（课件演示长方体的高变短了，同时变成两个面是正方形的长方体，如图6）

生：长方体的高变短了。

师：只是高发生了改变吗？

生1：长方体的形状也变了，面的大小也变了。

生2：有两个面变成了正方形。

师：你是怎么看出来的？

生：因为宽与高长度相等。

师：想一想，每个面分别是什么形状？每个面的长和宽分别是多少？

生：前面和后面是长方形、上面和下面是长方形、左面和右面是正方形。

师：当长方体的宽和高长度相等时，就会变成有两个面是正方形的特殊长方体。（课件演示长方体的长、宽、高都变成了4cm，如图7）现在是什么改变了？

生：长方体的长变短了，面和体都变小了。

师：什么发生了改变？

生1：每一条棱的长度都相等，每一个面都是正方形。

生2：长、宽、高相等，每一条棱长度一样，6个面完全相同。

师：所以，我们也说正方体是长、宽、高都相等的长方体。在此过程中，我们又研究了长方体的面的形状，长方体的面可能是长方形，也可能是正方形。

【评析】课件演示长方体长、宽、高的数据变化，使学生明白其中的变与不变，发现面、棱、顶点之间的关系，以及长方体与正方体之间的关系。

三、逆向思维，深化空间观念

（一）想象配面

师：这个长方体的长、宽、高分别是多少？想象一下，这个长方体的每一个面是什么样的？每一个面对应几号图形？请你完成平板电脑上的练习1（如图8）。

（二）自由拼图

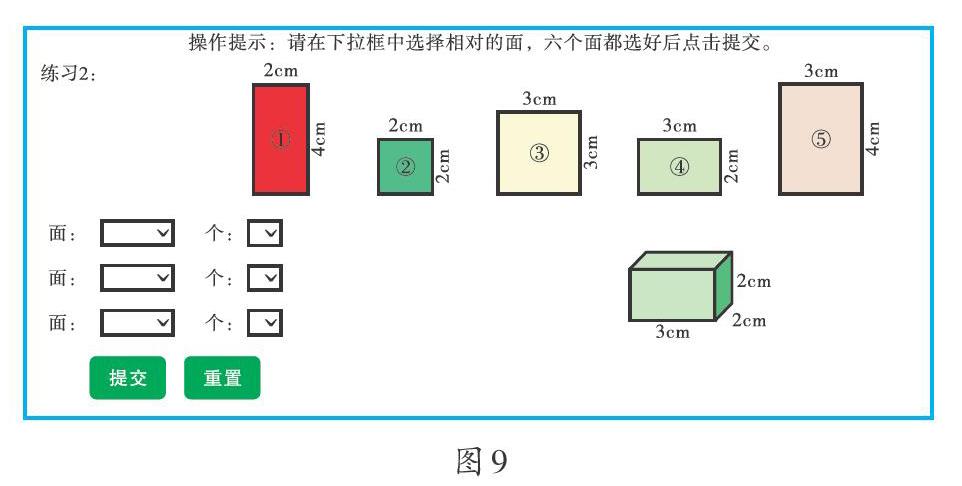
师：如果给你足够多的长方形和正方形，自由选择，你能不能围成一个长方体或正方体呢？需要用到几号面，需要几个面？请你在平板电脑上完成练习2（如图9）。

（三）文化拓展

师：（播放微课视频）今天我们从点、线、面的角度认识长方体，其实，我们的生活也离不开点、线、面，让我们继续在这个美丽而又神秘的风景中继续探索数学的奥秘吧！

【评析】学生利用平板电脑完成“给长方体配面”“根据图形搭建长方体”的练习。执教老师通过数据统计，了解学生掌握长方体知识的情况，及时调整教学策略，实现“以学定教”。

【总评】

数学是一门抽象且逻辑性强的学科，对于抽象的数学知识，有的学生理解起来比较困难。在这节课里，执教老师借助多媒体信息技术，将抽象的数学知识直观化、形象化，为学生理解数学概念提供了技术支持，促进了学生对数学概念的理解，具体体现在以下几个方面。

1.启发学生研究学习数学的方法。认识长方体是学生在小学阶段第一次深入地认识立体图形。面对一个立体图形，学生要从哪些方面着手研究？我们研究图形，一般把高维度的图形分解成低维度的元素，逐一了解图形的特征。开课伊始，执教老师利用课件动态演示点动成线、线动成面、面动成体的过程，化静为动，将图形的运动变化轨迹呈现在屏幕上，与教学结束前的视频“生活中的点线面体”前后呼应，让学生感知生活中事物组成的元素就是点、线、面、体，突出数学概念的本质属性，从而在头脑中形成一个知识网络，从中获得研究立体图形方法的启示。

2.发展学生的“空间观念”。“长方体的认识”是学生空间观念由二维向三维发展的转折阶段，引导学生由“面的认识”过渡到“体的认识”，是发展学生空间观念的重要媒介，是这节课的教学重点。执教老师利用3D软件将长方体进行旋转，把长方体的“外衣脱掉”，只剩下长方体的棱，有利于学生掌握长方体的特征;通过动态演示压缩长方体，让学生在数据的动态变化中感受正方体与长方体的关系，很好地培养了学生的空间观念。在平板电脑上给长方体“配面”这一环节，执教老师根据数据分析结果，了解学生掌握知识的情况，突破了教学难点。在动态几何软件及交互式网络程序的支持下，实现了“直观几何、实验几何与论证几何的结合”。

3.让学生成为学习的主人。为让不同学习层次的学生实现个性化学习、分层学习，更好地创设教师、学生、多媒体三向互动的环境，执教老师借助平板电脑呈现大量的学习资源，让学生自主发现、自主探索，同时根据学生“自学修改预学单”“给长方体配面”的情况进行数据统计，辨析难点，有利于了解学生掌握知识的情况，适时调整教学策略，实现“以学定教”的目的，同时也打破了时间和空间的界限，让学生可以随时利用互联网上的学习资源进行学习，使学生真正成为学习的主人。

（该课例获2019年全区中小学信息技术与学科教学深度融合优秀课例观摩评选活动一等奖）

（責编 欧孔群）