例谈数学抽象函数的解题方法
2020-04-18 06:18江苏省淮阴中学上官志薇
数学大世界 2020年6期
江苏省淮阴中学 上官志薇
一、理解符号,求定义域
定义域是学习和了解一个函数基础的、最先应该考虑的内容。因此,遇到抽象函数,我们首先应该理解题目中符号的意思,同时与学习过的基本初等函数进行归纳和对比,最终才能得出结论。
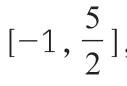
求解定义域是抽象函数问题中最容易理解的,但这并不代表对学生能力的要求有所降低。相反,学生更要理解定义域和取值范围之间的转化及具体定义,才能够正确、灵活地解题。
二、正确赋值,求解值域
对于抽象函数问题来说,题中的已知条件一定是足够充分的。求解值域与求解单调性等问题不同,它对于临界值的要求更高,并不仅止步于趋势。因此,学生一定要学会根据条件和函数特点正确赋值,才能求解值域。
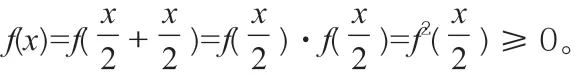
由此可以看出,对于像0、1 等比较特殊的数字来说,一定要先根据运算规则进行计算,才能为后面的求解打开思路。同时,大家还得注意,赋值并不仅局限于“值”,合理赋“符”和“字母”也是求解的关键。
三、转化变量,求解析式
对于函数来说,因变量随着自变量的改变而变化。因此,在已知抽象函数解析式特征的情况下,我们可以通过转化变量进行代数式相消,从而简化表达形式,最终得到函数的解析式。
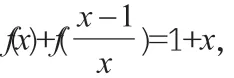
很显然,如果不清楚转化变量的方法,学生求解抽象函数解析式时将会没有方向。同时,每一道题目的转化方式也不可能完全相同,因此,教师一定要鼓励和引导学生多多计算和练习,才能熟练掌握。
函数的性质和表达式本就是多变的,同样的,抽象函数的变通性也很强。但是万变不离其宗,抽象函数的解决都离不开定义域、值域和表达式这几个方面。因此,只要大家仔细琢磨、勤加练习,就一定能够学好这个知识点。
猜你喜欢
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
语数外学习·高中版上旬(2022年2期)2022-04-09
语数外学习·高中版上旬(2020年10期)2020-09-10
读写算(2019年5期)2019-09-01
上海师范大学学报·自然科学版(2018年3期)2018-05-14
理科考试研究·高中(2017年10期)2018-03-07
中学课程辅导·教学研究(2017年29期)2018-02-26
中学生数理化·高一版(2017年1期)2017-04-25
中学生理科应试(2016年7期)2016-05-14
理科考试研究·高中(2016年9期)2016-05-14

