基于对角相似变换的不可约非负矩阵谱半径算法及其应用

商钰莹，张美黎，刘桂敏，吕洪斌

(北华大学数学与统计学院，吉林 吉林 132013)

非负矩阵谱半径的估计与计算在数值代数中具有重要意义，并且在特征值估计理论、矩阵级数的收敛分析、控制理论中都有着极为重要的应用，有助于线性方程组的收敛性分析和一些实际问题的稳定性分析.关于不可约非负矩阵谱半径的计算，文献[1-4]给出了不同的算法.本文将给出一种基于正对角相似变换的不可约非负矩阵谱半径的算法，并讨论算法的应用.

1 算法构造

定义1[5-6]设A∈n×n，如果存在n阶置换矩阵P，使得其中A11为r(1≤r≤n-1)阶方阵，A22为n-r阶方阵，则称矩阵A是可约的，否则称矩阵A是不可约的.

关于非负矩阵谱半径的界，有著名的Perron-Frobenius定理:

容易证明以下引理：

类似于文献[1]的证明有:

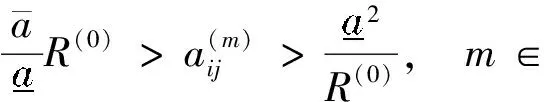
由引理3知

2 主要结果

因为A不可约，所以其有向图Γ(A)是强连通的[5-6].又对∀m∈+，A与A(m)有相同的零元模式，所以Γ(A(m))也是强连通的.

(1)

由式(1)，类似地有

进一步有

⋮

因此，∀i∈N，有

进一步，∀k∈+，有

3 数值算法及分析

根据上述迭代矩阵的构造过程和定理2，对不可约非负矩阵A的谱半径ρ(A)有如下算法.

算法1:

步1 给出不可约非负矩阵A=(aij)n×n，ε>0；

步3 如果rmax-rmin<ε，则转步5，否则取ε′≤α<1，其中ε′∈(ε，1)，转步4；

步5 输出ρ(A)=(rmax+rmin)/2.

下面应用MATLAB通过具体例子分析上述算法.

例1

表1 不同算法计算ρ(A)的迭代次数比较Tab.1 Comparison of iteration numbers of ρ(A) calculated by different algorithms

由例1可知，算法1更具一般性，适用于所有不可约非负矩阵谱半径的计算，且参数选择更方便，由于在迭代的每步引入了一个变参数，因而大大减少了迭代次数，提高了计算效率.

4 应 用

作为应用，我们讨论M-矩阵[5-6]最小特征值的计算和M-矩阵(广义对角占优矩阵[5-7])的迭代判别.

定义2[5]设A∈Zn×n={A=(aij)∈n×n:aij≤0，∀i≠j}，则A可以表示为

若s≥ρ(B)，则称A为M-矩阵；若s>ρ(B)，则称A为非奇异M-矩阵.

定义3[6]设A=(aij)∈n×n，若

|aii|≥r′i(A)， ∀i∈N，

则称A为对角占优矩阵；若上式均为严格不等式，则称A为严格对角占优矩阵；若存在正对角阵D，使AD为严格对角占优矩阵，则称A为广义严格对角占优矩阵，也称A为非奇异H-矩阵.

定义4[6]设A=(aij)∈n×n，定义m(A)=(mij)∈Zn×n，其中

称m(A)为A的比较矩阵.

定理3[5]设A=(aij)∈n×n，则A为广义严格对角占优矩阵的充要条件是A的比较矩阵m(A)为非奇异M-矩阵.

M-矩阵的迭代判别法：

算法2:

步1 输入不可约矩阵A=(aij)∈Zn×n，ε′≤α<1，其中ε′∈(0，1);

步2 如果aii>0，i∈N，转步3，否则转步7;

步7 输出‘A不是M-矩阵’;

步8 输出‘A是M-矩阵’，D=D(0)D(1)…D(m).

以上我们给出了不可约M-矩阵的迭代判别法，应用定理3和算法2自然可给出不可约矩阵为广义对角占优矩阵的迭代判别法.