盾构隧道下穿铁路线轨面沉降规律分析

秦 虎，马 亢，2，李科技

(1. 河西学院 土木工程学院，甘肃 张掖 734000；2. 重庆永宏岩土工程有限公司 重庆 404100)

0 引言

随着城市化建设进程的加快，为了缓解城市交通压力，城市轨道交通线网规模不断增大，下穿既有公路、铁路、防洪堤、房屋建筑等的工程越来越多，引起了国内外学者的广泛关注.由于地铁盾构隧道的施工修建，必然会引起各类近接建(构)筑物的沉降变形，从而影响其正常运行及安全使用，尤其是盾构上方存在既有运行的国家铁路客货线路更需值得高度重视，因为铁路是国民经济运行的生命线，不可中断运行且必须确保时刻运行安全，因此，对于盾构下穿铁路工程，必须要从最不利施工作业条件对下穿施工予以专项研究.

目前关于盾构隧道下穿工程的研究已有大量的文献报道.孙连勇等[1]以济南轨道交通 R3 线一期工程某区间隧道为背景，采用 Abaqus 软件建立数值模型模拟在不主动加固和加固两种工况下，盾构隧道近距离下穿胶济铁路线桥梁与路基引起的变形情况；赵勇博等[2]以福州地铁一号线(罗汉山站至福州火车站区间) 为依托工程，采用 MIDAS/GTS 有限元软件对盾构隧道下穿铁路轨道群引起的路基沉降进行了三维数值模拟分析；朱垚锋等[3]以珠机城际铁路盾构隧道下穿四孔箱涵为工程背景，采用参照规范、数值模拟和现场监测的方法，研究淤泥地层盾构隧道下穿箱涵引起的沉降；张安睿等[4]依托成都至贵阳高铁大方隧道工程，对高速铁路隧道下穿既有高速公路路堤影响进行研究；张坚等[5]研究了富水黄土地区暗挖地铁下穿既有建筑时地表和建筑的沉降特性及规律；管飞等[6]以南京市纬三路过江隧道工程为背景，研究了盾构下穿防洪堤引起的地层变形和地表沉降规律；张亚洲等[7]以南京纬三路过江通道工程S线大直径泥水盾构下穿保健村民房建筑群为背景，通过三维数值计算，对盾构施工主要影响区的范围和沉降量进行理论预测；唐新权[8]采用三维数值模拟方法对新建隧道下穿机场地下行包通道进行了沉降分析；汪珂等[9]依托地铁4号线区间隧道下穿和平门古城墙工程，研究了双线盾构下穿过程诱发地表沉降的规律及上部古城墙的变形特征.侯建林等[10]运用FLAC3D有限元软件对实际工程中盾构隧道开挖过程进行数值模拟，计算并对比在盾构隧道近距离下穿出入场线暗挖隧道的施工过程中暗挖隧道周边位移的变化规律； 张伟森等[11]利用R/S分析法对盾构下穿机场过程中的地表沉降的发展趋势进行了研究； 肖金花等[12]利用有限元软件PLAXIS 3D，基于土体HSS本构模型，针对常州地铁1号线盾构隧道开挖实际工况,分析了盾构施工对周围土层及地下管线的影响.

本文结合某市轨道交通5号线和平公园站至红钢城站区间盾构法隧道下穿国家客运主干线—武九铁路为工程实例，根据盾构施工的自身特点，按最不利因素情况下对下穿铁路开挖施工过程开展数值模拟研究，重点检验在既定施工方案下，因盾构施工引起的铁路轨面沉降及其分布规律，判断其是否处于国家相关规范安全范围之内，以为实际工程中及时调整作业方案、技术措施提供科学依据，也可为今后类似施工案例积累工程经验.

1 工程概况

和平公园站至红钢城站区间隧道沿和平大道地下穿行，区间隧道位于和平大道高架(建设六路跨线桥)西北侧，区间左线长1233.0m，右线长1231.7m，左CK25+801.260处设长链1.260m，区间线间距为10.0～15.2m，区间隧道在右ZK25+358.031～右ZK25+380.479(22.45m)范围内下穿武九铁路，交角约32度，区间隧道穿越武九铁路线平面示意图如图1所示.隧道覆土厚度约为18.0m.下穿段场地地层从上至下依次为杂填土、淤泥质土、粉土、粉砂、粉质黏土互层、粉细砂. 根据本次钻探、原位测试及室内试验结果，结合拟建工程特性，对场地内各地基土层的工程性能分述如下：

1)杂填土：填土成份复杂，主要为沥青混凝土路面及其下伏碎石土垫层，密实度不均匀，力学强度差异大.

2)淤泥质粉质粘土：天然含水率为36.9%，天然重度为18.0kN/m3，孔隙比为1.039，液性指数为1.01，主要呈软塑状，局部流塑状.压缩模量Es0.1-0.2为3～4MPa，具高压缩性；天然快剪抗剪强度C值为10～15kPa，φ值为6°～8°.

3)粉质粘土：天然含水率为35.6%，天然重度为18.1kN/m3，孔隙比为1.006，液性指数为0.96，主要呈软塑状，局部可塑状.压缩模量Es0.1-0.2为7～9MPa，具中等偏高压缩性.天然快剪抗剪强度C值为15～16kPa，φ值为14°～15°.

4)粉细砂：天然含水率为19.9%，天然重度为19.9kN/m3，孔隙比为0.588，以中密为主，局部稍密.石英含量为30%～40%.压缩模量Es0.1-0.2为14～16MPa，具中等偏低压缩性；天然快剪抗剪强度C值为0kPa,φ值为30°～31°.

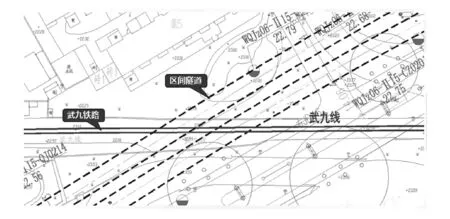
图1 区间隧道穿越武九铁路线平面示意图

2 变形控制标准

下穿武九铁路线均为有砟道床结构，隧道下穿段铁路设计时速160～250km/h.《高速铁路设计规范》(试行)(TB10621-2014)明确给出了工后沉降的定义和桥梁工后沉降量及差异沉降量限值要求，对于本工程涉及到的铁路为有砟轨道，因此，控制的墩台均匀沉降为30mm，相邻墩台的沉降差为15mm,轨面沉降值不得超过9mm,相邻两股钢轨水平高差不得超过5mm,相邻两股钢轨三角坑不得超过4mm,前后高低(纵向水平)5mm.

3 数值模型分析

3.1 计算模型建立

区间隧道在右ZK25+358.031～右ZK25+380.479(22.45m)范围内下穿武九铁路.区间隧道在此处为盾构隧道形式.左线隧道与右线隧道净距为3.85m，隧道埋深为17.86～18.04m.

为了研究盾构隧道掘进对武九铁路的影响，采用FLAC3D软件建立三维模型，本区间下穿隧道采用实体单元进行建模，列车荷载简化为均布条形荷载施加在铁路双股轨道范围内(宽度1.45m)，采用实体单元进行超重模拟，隧道穿越各岩土体采用实体单元，本构模型采用M-C弹塑性模型.盾构管片结构采用弹性模型进行计算.本次计算分析基于FLAC软件的连续介质的有限差分计算方法，对于盾构掘进范围的土体瞬时变为空单元(NULL)即刚度置0以模拟开挖过程，此时隧道围岩应力场进行二次重分布，施作完管片衬砌后，围岩应力发生三次重分布，直至施工全部结束，土体应力最后调整稳定，以此计算得到轨面沉降.管片外径6.2m，内径5.5m，衬砌厚度0.35m，选用C50高强混凝土.

模型沿盾构隧道水平径向为x方向，开挖推进方向为z方向，竖直方向为y方向.前后左右边界约束相应法向方向位移，底部边界约束z方向位移，顶部边界为自由面.

地层岩土体物理力学参数采用地铁穿越铁路线最近地质钻孔揭示的岩土情况并根据勘测报告取用，计算参数取值见表1, 并据此钻孔揭示的岩土体分布特征建立有限元计算模型.

表1 计算参数取值

隧道下穿武九铁路下方，交角约32°.为了研究隧道动态施工作用下的铁路轨面沉降规律，沿武九铁路轨面位置(正穿地铁线位下方)设置9个沉降关键特征点，计算模型平面图及轨面沉降关键点布置见图2，模型计算范围为78×70×45m3，模型采用32 397个实体单元，32 187个节点，三维有限元计算模型、区间隧道与穿越铁路关系分别见图3、图4所示.

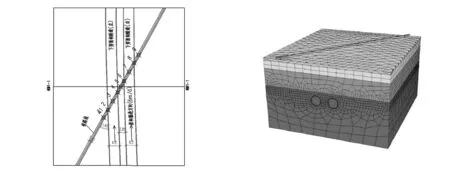
图2计算模型平面图及轨面沉降关键点布置 图3三维有限元计算模型

图4 区间隧道与穿越铁路关系

3.2 盾构隧道施工模拟

计算对双线盾构隧道施工进行全过程模拟，按双隧同步每天约4环(即6m/d)进度对穿越铁路线全过程进行数值模拟，共模拟开挖13天，每天为一个开挖步，共计13个开挖步，隧道推进总距离为78m，具体如下：

1)双线隧道掘进30m(5天即5个开挖步)，到达铁路线位下方；

2)双线隧道继续掘进18m(3天即3个开挖步)，穿越武九铁路线位范围；

3)双线隧道继续掘进30m(5天即5个开挖步)，隧道完全通过武九铁路线影响范围.

3.3 计算结果分析

图5是和平公园站至红钢城站区间盾构隧道通过武九铁路后轨面的位移云图.

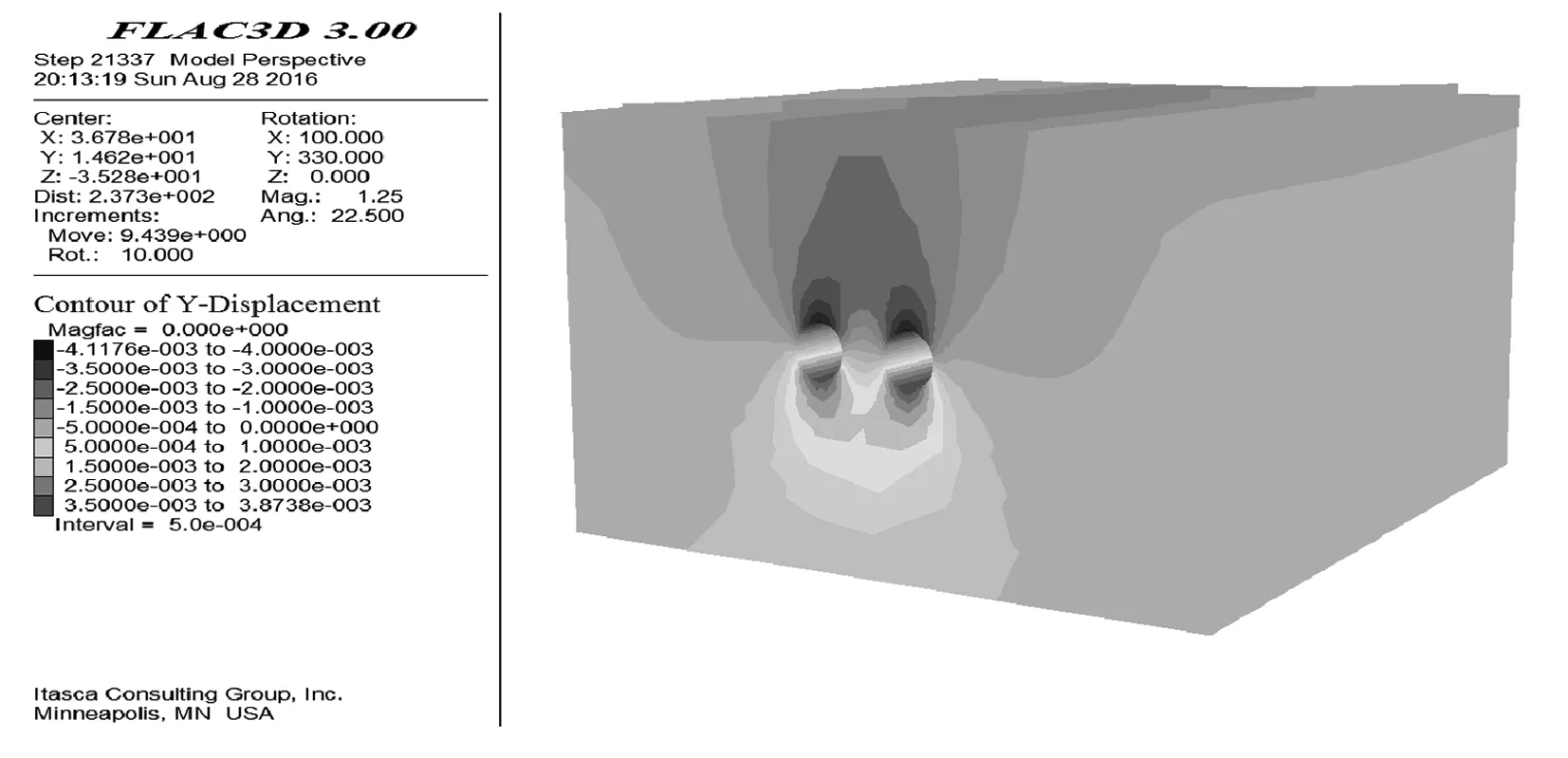
图5 隧道全部开挖完成后轨面位移云图

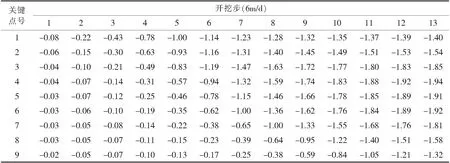
隧道在开挖过程中，武九铁路线轨面9个关键特征点的沉降变化曲线如图6所示.

图6中显示了本区间隧道在通过武九铁路轨面沉降变化规律.从图6中可以看出：地铁区间隧道施工产生的沉降不是瞬间沉降，而是一个变化累积的过程.隧道在开挖至隧道开挖结束，铁路线轨面上各关键点的沉降变形均处于一个不断递增的过程，当隧道掘进至铁路线下方时(5至9步)，沉降变形出现一个陡增的态势，之后沉降速率变为平缓.当隧道开挖全部结束时，铁路线轨面关键点的最大沉降位移值约为1.94 mm(最大沉降点出现在4、5、6号关键点，即整个双线隧道中线范围正上方对应的铁路线轨面位置)，整个开挖过程中铁路线轨面上各关键点的沉降变化值具体见表2.

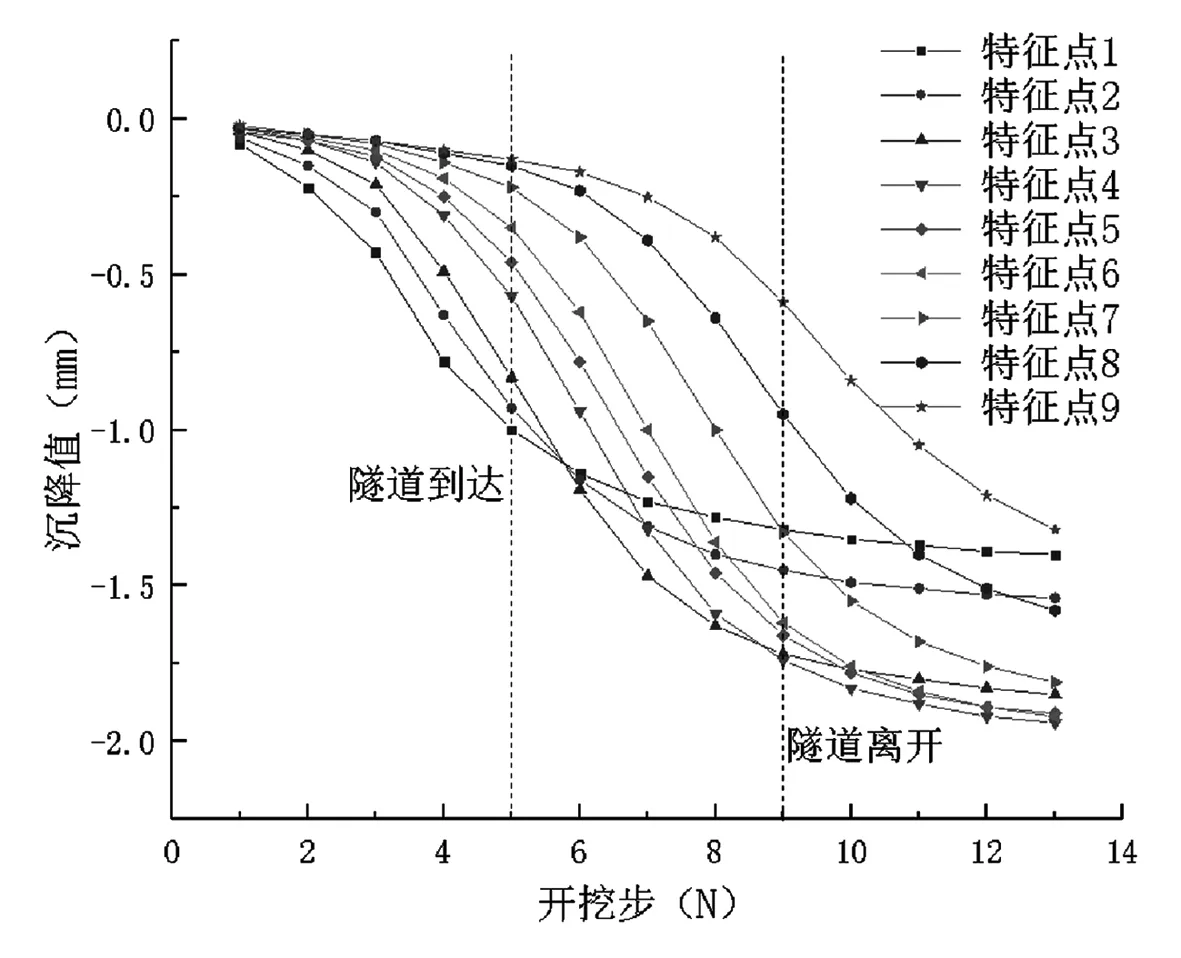
图6 铁路轨面9个关键点沉降变化曲线

根据以上计算结果显示，在隧道开挖的整个过程，铁路线最大竖向位移为1.94mm，穿越隧道范围铁路线纵向沉降差最大值为0.62mm，盾构隧道围岩的最大竖向位移为4.12mm，满足高铁、城际铁路及动车线铁路轨面工后均匀沉降量不大于9mm的安全要求.

4 结论

本文针对某市轨道交通5号线和平公园站至红钢城站区间隧道下穿武九铁路施工，建立了三维数值模型，开展了隧道下穿施工对铁路轨面沉降影响的模拟分析，得到如下结论：

1)在区间盾构隧道施工过程中，武九铁路轨面沉降值均小于2.0mm，满足《高速铁路设计规范》(试行)(TB10621-2014)要求沉降不大于9mm的控制值，最大竖向变形满足相关要求，盾构隧道施工不会影响既有武九铁路的正常安全运营.

2)盾构法隧道在掘进过程中，需进行同步注浆和二次注浆，加之掘进过程中盾构对作业面的推力，事实上这些是对减小铁路轨面沉降均是有利的，本文是模拟在最不利情况下，即未考虑注浆加固，未考虑掌子面推力等有利因素下的铁路沉降规律.并且，此次计算的是铁路轨面最终沉降量，未考虑时间效应，对于掘进速度(排土量、扭矩、千斤顶推力)、土体损失、土体流变等因素假设均为瞬时一次完成的，即每开挖步范围内土体是一次开挖完成(刚度为0)，因此本次计算得到的沉降及各类变形指标均为最大终值.

3)本次计算是基于FLCA3D软件得到的铁路轨面沉降及变形规律，虽不能代表实际精确结果，但基本反映了铁路轨面沉降的“量级、正负号(沉降及隆起)、变化规律”这三个方面的定性认识，在实际工程中还应结合现场监测数据、工程运行情况等多方面加以完善，以不断改进下穿铁路的施工方案、技术措施等.