基于交叉效率DEA与群体共识的区间乘性语言偏好关系群决策

刘金培，杨宏伟，陈华友，周礼刚

(1.安徽大学商学院，安徽 合肥 230601； 2.北卡罗莱纳州立大学工业与系统工程系，美国 罗利 27695；3.安徽大学数学科学学院，安徽 合肥 230601)

1 引言

在群决策过程中，决策者们对备选方案经常给出方案两两比较的偏好关系，常见的主要有数值型偏好关系和语言型偏好关系两类[1]。面对实际决策问题，决策者们更加习惯于以语言的方式给出自己的知识和偏好[2]。近年来，针对语言偏好关系群决策问题的研究已经成为人们关注的热点[1-14]。

决策者们给出的语言偏好关系往往不能满足一致性要求，为了对语言偏好关系的一致性进行改进，人们提出了多种一致性调整的方法。Wang和Xu[3]提出了一种使语言判断矩阵达到弱一致性的调整算法。Dong等[2]则以调整量最小为目标，建立带0-1变量的优化模型来修改语言偏好关系的元素使其达到一致性要求。文献[4]给出两种语言偏好关系加性一致性迭代逼近修正算法。Liu等[5]结合二元语义表示，提出一种新迭代算法来提高语言偏好关系的一致性。靳凤侠和黄天民[6]则通过构造循环圈矩阵来进行语言偏好关系一致性的调整。

由于实际问题的复杂性、决策者信息不足和时间限制等原因，决策者们往往不能给出精确的语言偏好信息，而是以区间语言偏好关系的形式给出[8-14]。针对区间语言环境下的群决策问题，文献[8]定义了群体共识测度，用来度量单个偏好与群体偏好的贴近度。Chen等[9]则用相容性指标度量个体与群体偏好的差异，并提出基于群体相容性的专家赋权方法。文献[10]和文献[11]分别利用LCOWA算子和LCOWGA算子将区间加性语言信息和区间乘性语言信息集成为单值的语言术语，然后基于群体相容性提出加性和乘性语言偏好环境下的群决策模型。Xu和Wu[12]定义区间语言偏好关系的群体共识测度，并给出一种基于群体共识的偏好关系调整算法。Meng等[13]则定义了区间语言偏好关系一致性的新测度，同时构建基于新测度的偏好关系调整算法。

从已有研究来看，目前关于区间语言偏好关系的群决策还存在以下问题：一是目前普遍应用一致性调整的方法来对区间语言偏好关系进行调整，然而调整算法修改了专家给出的原始信息，使决策结论的可靠性难以保障[15]。二是目前针对区间语言信息，往往将区间语言信息集成为单个语言术语或仅利用了区间的单侧边界值，这造成了决策信息的严重丢失。三是已有的群决策专家赋权模型均基于专家给出的原始区间语言偏好信息，而决策过程中专家给出的区间信息往往不能全部利用，因此需要设计更加合理的基于信息提取的动态赋权方法。

针对以上问题，本文构建基于理想点的交叉效率DEA模型和基于群体共识的赋权模型，在此基础上提出一种基于Monte Carlo随机模拟的区间乘性语言偏好关系群决策方法。首先，提出乘性语言偏好关系导出函数的定义，并构建产出导向的DEA模型，证明一致性乘性语言偏好关系DEA效率得分与排序向量之间的内在关系。在此基础上，建立基于理想值的交叉效率DEA模型，提出乘性语言偏好关系的通用排序方法。针对群体区间语言偏好关系，按照均匀分布提取一般语言偏好关系，然后基于群体共识建立目标规划模型以获取各语言偏好关系的权重系数。最后，利用Monte Carlo随机模拟的方法对整个群体偏好空间进行统计分析，得到群决策期望排序向量及其可信度。算例分析表明本文方法解决了区间语言偏好关系在决策过程中信息损失的问题，具有较强的适用性和较高的可信度。

2 基本概念

在群决策中，方案集为X={x1,x2,…,xn}，专家对于备选方案集X中的多个方案进行两两比较，依据乘性语言术语集S，给出语言偏好关系矩阵P=(pij)n×n。其中，乘性语言术语集S={sα|α=1/t,…,1/2,1,2,…,t}，S中元素的个数2t-1称为语言术语集的粒度，t为大于1的自然数。当t=5时，我们有：

S={s1/5=extremely low,s1/4=very low,s1/3=low,s1/2=slightly low,s1=medium,s2=slightly high,s3=high,s4=very high,s5=extremly high}.

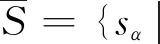
在专家依据乘性语言术语集S所给出的语言偏好关系矩阵P=(pij)n×n中，pij=sα∈S表示方案xi相对方案xj的重要性程度(i,j=1,2,…,n)。当α>1时，表示方案xi比方案xj重要，当α<1时，表示方案xj比方案xi重要，且随α取值的增加，重要的程度也越大。当α=1时，表示方案xi与方案xj同等重要。

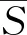
pij⊗pji=pii=s1，i,j=1,2,…,n

(1)

则称P=(pij)n×n为乘性语言偏好关系。

定义2[17]：若乘性语言偏好关系P=(pij)n×n中的元素pij满足：

pik⊗pkj=pij,i,j,k=1,2,…,n

(2)

则称该乘性语言偏好关系满足乘性一致性。

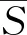
在保持乘性语言偏好关系信息不损失的前提下，提出如下导出函数的定义：

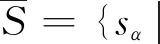
rij=φ(pij)=(2t-1)logtT(pij),i,j=1,2,…,n

(3)

则称函数φ为乘性语言偏好关系的导出函数，R=(rij)n×n为乘性语言偏好关系P=(pij)n×n的导出矩阵。

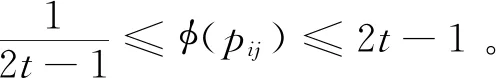
定理1若乘性语言偏好关系P=(pij)n×n满足乘性一致性，则其导出矩阵R=(rij)n×n也满足乘性一致性。

证明：若乘性语言偏好关系P=(pij)n×n满足乘性一致性，由定义2得：

rii=φ(pii)=(2t-1)logtT(pii)=1,

i=1,2,…,n.

rij·rji=φ(pij)·φ(pji)

=(2t-1)logt(T(pij)·T(pji))=1,

i,j=1,2,…,n

因此，导出矩阵R=(rij)n×n为乘性偏好关系，进一步有：

rik·rkj=φ(pik)·φ(pkj)

=(2t-1)logt(T(pik)·T(pkj))=(2t-1)logtT(pij)=φ(pij)=rij,i,j=1,2,…,n.

所以，导出矩阵R=(rij)n×n满足乘性一致性。证毕。

由上述分析可见，导出矩阵与原乘性语言偏好关系存在着严格的对应关系。同时，导出函数在将乘性语言偏好关系转化为实值乘性偏好关系的同时，既满足单调性和有界性的要求，又可保证原始语言偏好关系的传递性。

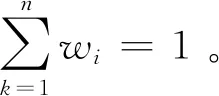
φ(pij)=wi/wj

(4)

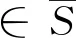
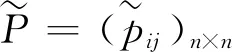
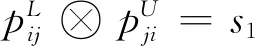
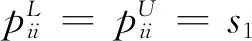
(5)

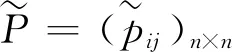
3 区间乘性语言偏好关系的群决策方法

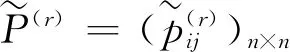
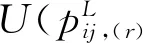
3.1 基于交叉效率DEA的乘性语言偏好关系排序

本节提出一种基于交叉效率DEA的乘性语言偏好关系排序方法，该方法可以避免对偏好关系进行一致性调整。设P=(pij)n×n为方案集X={x1,x2,…,xn}上的乘性语言偏好关系，现将各决策方案均视为一个独立的决策单元(DMU)，即将决策方案xi作为决策单元DMUi，且与偏好关系P=(pij)n×n中的第i行相对应(i=1,2,…,n)。若决策者认为方案xi比方案xj重要，则对于∀k∈{1,2,…,n}，有pik>pjk，进而满足φ(pik)>φ(pjk)，可见导出矩阵的每一列均可视为决策单元的每一类产出。同时，我们将φ(s1)作为每个决策单元的虚拟投入。此时，便得到偏好关系P=(pij)n×n对应的投入产出，如表1所示。

由表1，建立基于产出的CCR模型(Out-oriented)，对方案决策xd进行效率评价，d=1,2,…,n，具体形式如下：

maxθd

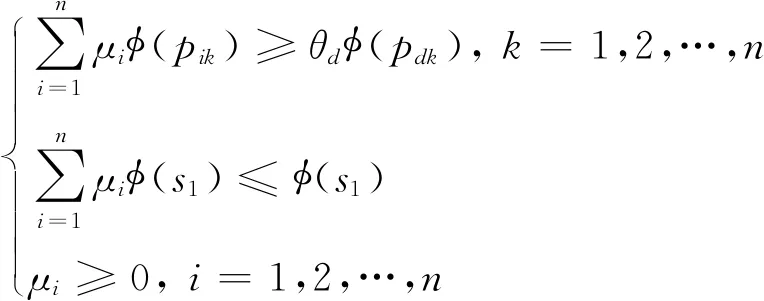
(6)

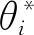
证明：若P=(pij)n×n满足乘性一致性，由式(4)，模型(6)可转化为：

maxθd

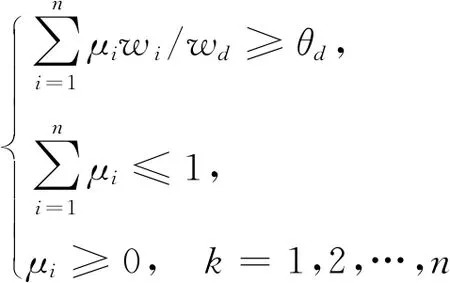
(7)

对任意d=1,2,…,n，将μd=1-μ1-…-μd-1-μd+1-…-μn带入模型(7)中第1个约束条件，得：

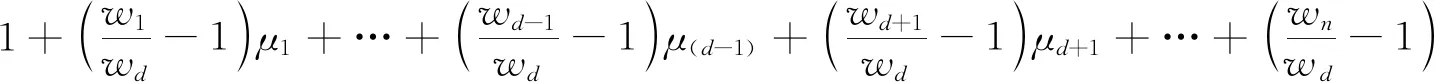
(8)

定理2说明对于满足一致性的乘性语言偏好关系，可由计算各方案的DEA效率值得到偏好关系的排序向量。然而在实际决策过程中，专家给出的乘性语言偏好关系往往不满足一致性条件。为了解决该问题，我们建立交叉效率DEA模型，将各方案自评价效率和他评价效率的均值作为方案的最终效率评价值，进而计算其排序向量。

首先，先求得决策单元的自评价效率值。基于表1建立投入导向的DEA模型，来求得所有决策单元自评价效率得分，DMUd(d=1,2,…,n)的自评价效率得分值θdd通过模型(9)求得：

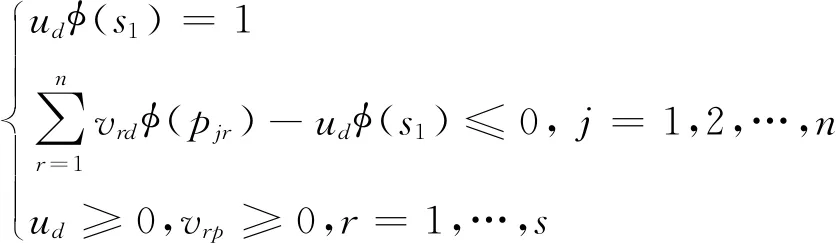
(9)

其中，ud表示决策单元投入的权重，vrd(r=1,2,…,n)表示第r个产出的权重。

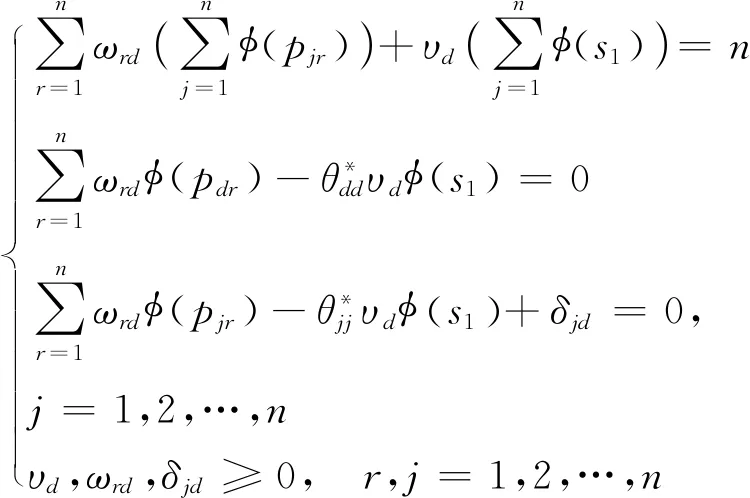
(10)

进一步，结合各方案自评价与他评价效率值，可得方案的最终交叉效率评价值为：

(11)

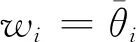
3.2 基于群体共识的专家信息赋权模型

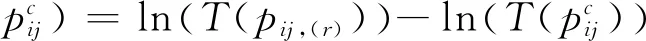
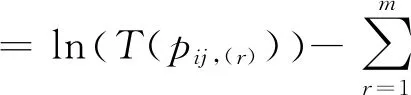
(12)

来表示单个偏好与群体偏好的差异。以群体共识为目标，建立下列专家信息赋权模型，使得个体偏好与群体偏好的差异最小化。

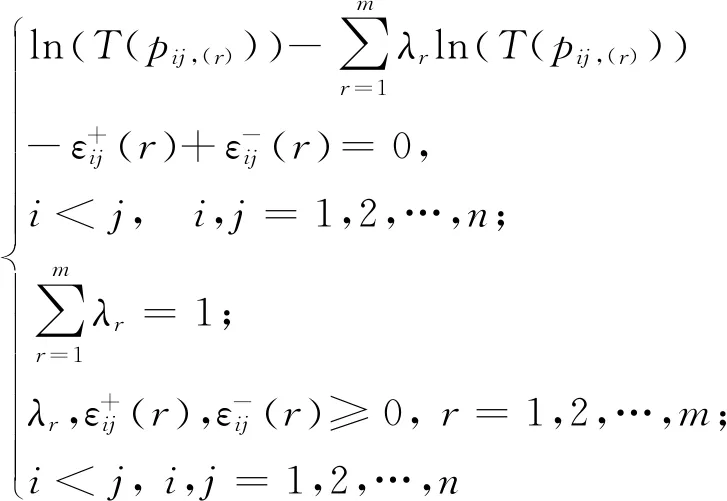
(13)

求解模型(13)，即可得到提取到的m个乘性语言偏好关系矩阵的最优权重系数。

此时，我们便可由提取到的m个乘性语言偏好关系P(r)=(pij,(r))n×n(r=1,2,…,m)，求得群体决策的最终排序向量，流程如图1所示。

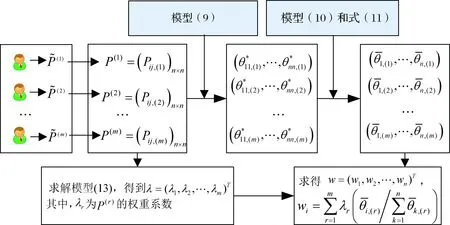
图1 群体决策方案排序向量计算流程图

具体步骤如下：

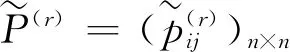
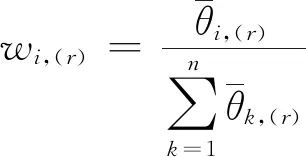
步骤3根据模型(13)计算m个乘性语言偏好关系P(r)=(pij,(r))n×n的权重系数，记为λ=(λ1,λ2,…,λm)T；

步骤4将从m个语言偏好关系中得到的排序向量进行集成，得到最后的排序向量w=(w1,w2,…,wn)T，i=1,2,…,n.

(14)

根据上述步骤，对随机向量Y的每一个可能取值，我们都可以得到其对应的排序向量。

3.3 基于随机分析的区间乘性语言偏好关系的群决策

基于交叉效率DEA和群体共识模型，我们已经提出一种乘性语言偏好关系的群决策排序向量的计算方法。进而针对随机向量Y的所有可能取值，利用Monte Carlo模拟进行统计分析来进行区间乘性语言偏好关系的群决策。

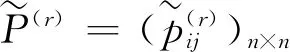
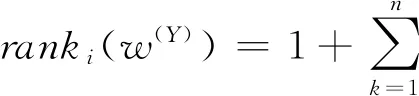
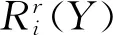
(15)

(16)

根据群决策期望排序向量，可以知道xi的期望排序结果为：

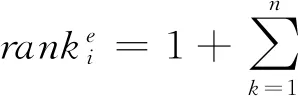
(17)

进一步，在整个群决策偏好空间内，对期望排序结果成立的子空间进行积分，便得到方案xi期望排序的可信程度为：

(18)

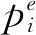
可以看出，基于随机分析的区间乘性语言偏好关系群决策方法分析了群决策偏好空间内所有可能，避免了信息的丢失，同时模型(13)计算偏好信息权重系数时完全基于每次提取到的语言偏好信息，为一种动态赋权方法。因此，本文提出的群决策方法更具合理性。

4 算例分析

近年来，我国经济建设取得了举世瞩目的成就，外商直接投资(FDI)起到了重要的推动作用，然而部分项目导致环境受到严重破坏。为了规范地方政府招商引资行为，环保部门需要对引入的外商企业和资产的环境保护技术和能力(以下称为环保能力)进行评价和择优。现将4家招商引资企业：制造型外资企业(x1)，服务型外资企业(x2)，咨询类外资企业(x3)和外资环保科技公司(x4)。根据环保能力进行排序和择优。环保部门聘请4位专家根据经验对这4个企业进行评价，评价依据的语言术语集为：

S={s1/5=极差,s1/4=非常差,s1/3=差,s1/2=稍差,s1=无差别,s2=稍好,s3=好,s4=非常好,s5=极好。}

4位专家给出的区间语言偏好关系分别为：

根据本文所提出的方法，在群体区间乘性语言偏好空间内基于均匀分布随机生成乘性语言偏好关系，建立基于交叉效率DEA模型和群体共识赋权模型，根据图1的流程得到每次提取的排序向量结果。利用Monte Carlo多次模拟，求得最后的期望排序向量，并给出其可信度。模拟不同次数时，得到结果如表3所示。

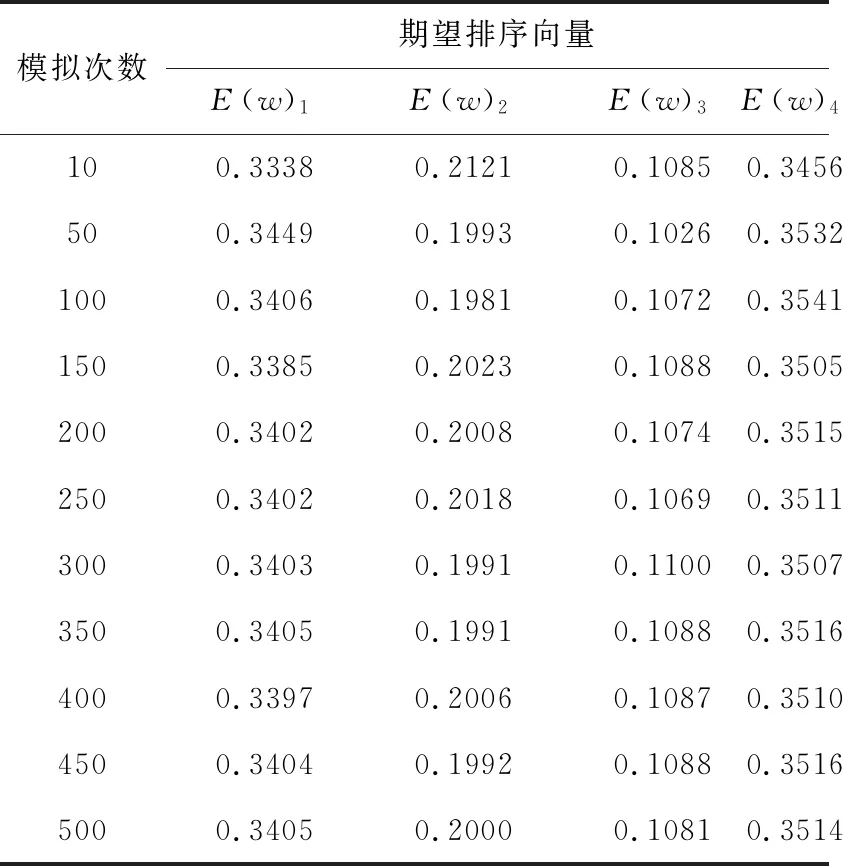
表3 不同模拟次数下的期望排序向量

根据表3可知，当模拟次数超过300次后，排序向量的期望值趋于稳定，变化范围小于0.002。选取模拟次数为500时，统计x1、x2、x3和x4的期望排序向量及其可信度，见表4。

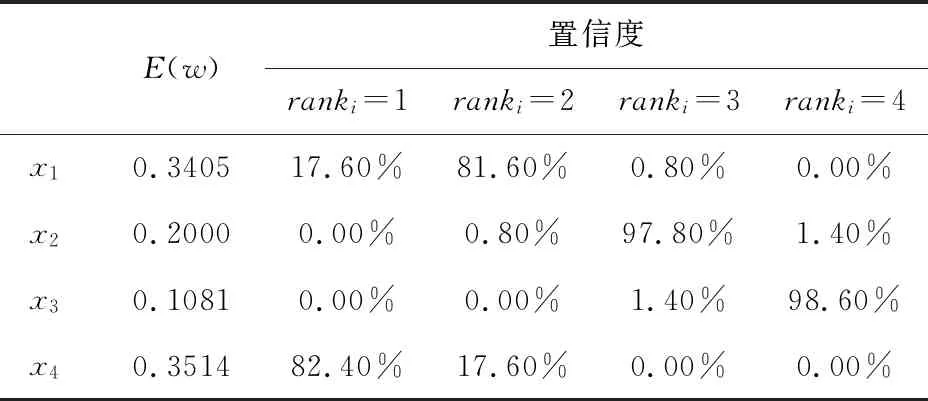
表4 各企业环保能力期望排序和可信度

根据500次随机模拟所得各种情况的排名统计，做出排名统计频率分布图，如图2所示。

根据期望排序向量可知，4个企业之间的环保能力排序结果为：x4≻x1≻x2≻x3。根据计算结果，可以确定第四企业(外资科技公司)的环保能力最佳，其排名第1的可信度为82.40%，应优先考虑引入该类具有绿色低碳技术的外资企业。

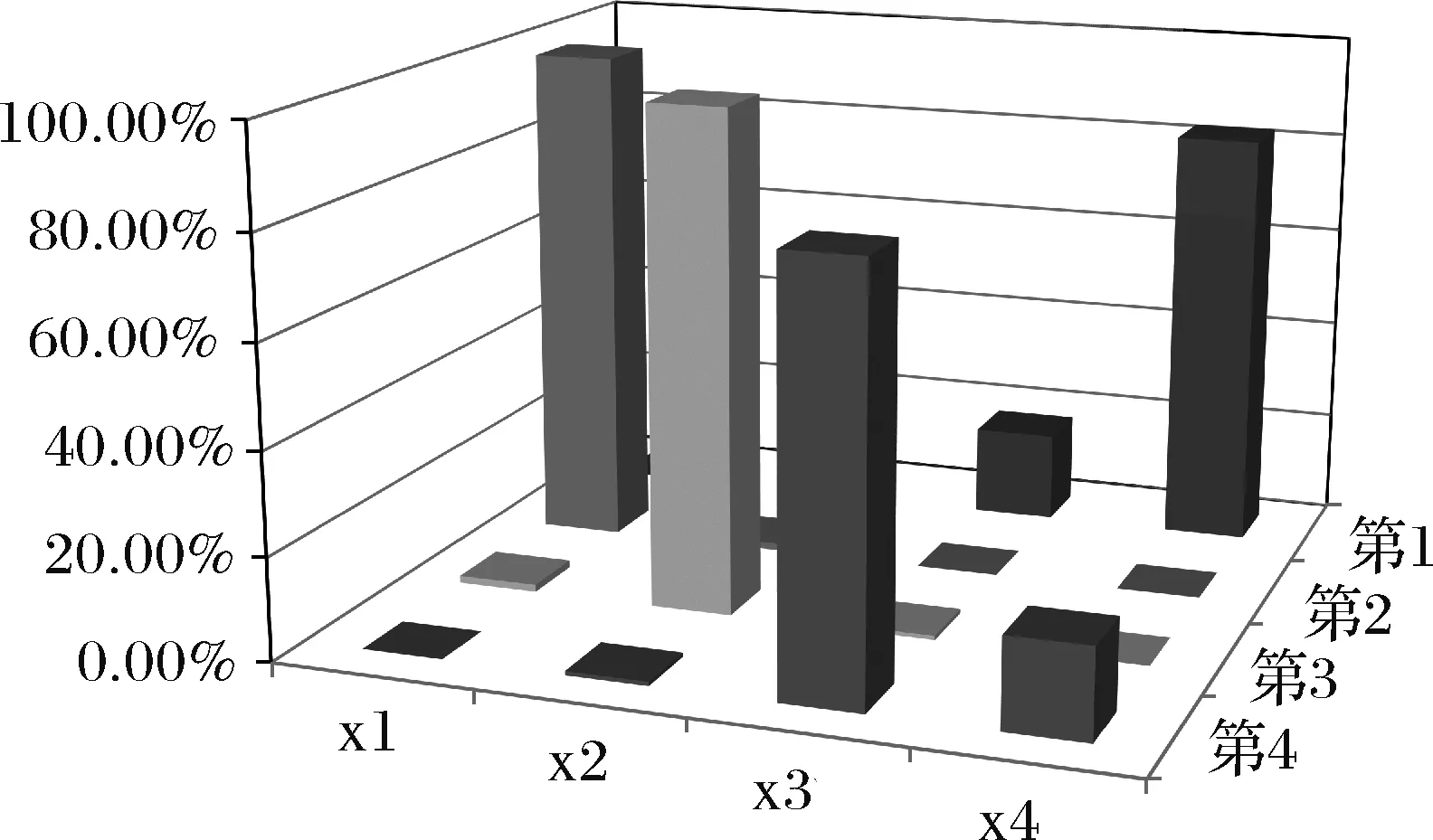
图2 四个企业排名统计频率分布图

5 结语

本文针对目前语言偏好信息环境下群决策方法中的缺陷，如一致性调整算法修改了专家给出的原始信息造成决策结论的可靠性不高，将区间语言信息集成为单个语言术语致使决策信息的严重丢失等问题，提出了一种新的基于交叉效率DEA模型和群体共识的区间乘性语言偏好关系群决策方法。将各决策方案均视为DEA决策单元，构建基于理想值的交叉效率DEA模型，提出乘性语言偏好关系的通用排序方法。针对群体区间乘性语言偏好关系，按照均匀分布提取一般语言偏好关系，然后基于群体共识建立目标规划模型计算各语言偏好关系的权重系数。利用Monte Carlo随机模拟的方法对整个群体偏好空间进行统计分析，得到群决策各方案的期望排序向量及其可信度。本文方法不需要对语言偏好关系进行一致性调整，解决了区间语言偏好关系在决策过程中信息损失的问题，具有较强的适用性和较高的可信度。