生产规模不经济性条件下考虑消费者偏好的智慧供应链扶贫模型研究
万骁乐,王 茜,孟庆春,杜元伟
(1.中国海洋大学管理学院,山东 青岛 266100;2.山东大学管理学院,山东 济南 250100)
1 引言
“精准扶贫、精准脱贫”是十八大以来党中央扶贫工作的基本方略。为了更好的实现造血式扶贫,各大电商平台发挥“大数据”的优势,积极投入到扶贫工作中,为农户提供智慧化的服务,拓宽销售渠道。例如:京东的“扶贫馆”、苏宁的“电商扶贫实训店”等。因此,借助智慧供应链更好的开展扶贫工作已成为一种重要的扶贫手段,并取得积极成效。例如,2017年12月以来,国家级贫困县在阿里智慧供应链平台的商品交易总额已经达到541亿元。京东逐渐探索出智慧供应链扶贫创新模式。截止到2018年第二季度,京东在全国832个贫困县上线商品实现销售额超300亿元。由此可见,利用智慧供应链平台进行现代化的智慧扶贫已经为扶贫的一条重要途径。智慧供应链不仅是精准扶贫工作的重要抓手,也有利于降本增效,更好地连接生产与消费,促进供需匹配和消费升级[1]。现阶段,关于智慧供应链扶贫等新型扶贫方式的问题开始引起学者的广泛关注。例如:邓琦珑等[2]基于精准扶贫背景,构建"合作社+社会企业"扶贫供应链模型,设计成本共担契约进行帕累托改进,并提出政府的最优补贴策略。周艳菊等[3]考虑消费者扶贫偏好,以单个农民合作社、单个农产品加工商和单个电商平台组成的三级供应链结构,研究了企业扶贫对于供应链总利润和各成员利润的影响。
大数据云计算等技术促进电商平台向智慧供应链平台发展,将电商平台引入到供应链结构中并探究其决策问题的研究已取得较为丰硕的成果。例如:浦徐进等[4]通过构建制造商、实体店以及电商组成的双渠道供应链行为博弈模型,探究供应链定价策略及渠道模式对供应链成员利润水平的影响。Giri等[5]构建了电商平台负责销售、回收的双渠道闭环供应链模型, 探究其定价策略和回收决策。邵腾伟和吕秀梅[6]研究了电商平台下,生鲜农产品供应链纵向一体化众筹预售与众包生产联合决策机制。还有一部分学者讨论了考虑退货策略的电商平台供应链决策。例如:Li等[7]考察了电商平台分销商的退货政策、产品质量和定价策略对顾客购买和退货决策的影响,研究了不同情形下的直销商定价策略、退货策略和质量策略。陈崇萍和陈志祥[8]采用退货担保期权综合不同退货策略的优点,构建了网络销售中基于期权的退货与定价模型。李玉民等[9]通过构建包含生鲜电商的冷链宅配供应链模型,分别讨论了集中决策和分散决策下的退货期限、销售价格、新鲜度、保鲜努力程度、收费策略以及最优利润。除此之外,少数学者考虑到电商平台在供应链中的功能变化,对电商平台的决策进行了进一步的研究。例如,王玉燕和于兆青[10]考虑平台的特征变化,讨论了电商平台的公平关切行为下,电商闭环供应链的回收策略与协调机制。不难看出,上述文献从多维度探究了电商平台供应链的决策及协调问题,但是鲜少有人考虑扶贫供应链中电商平台服务水平的差异性对供应链决策的影响。事实上,在智慧供应链扶贫实践中,由于供应链主体(例如合作社、批发商、智慧供应链平台扶贫馆、政府机构)的差异性和复杂性,会引起扶贫供应链结构的差异化,扶贫模式也将有所不同。
消费者异质性偏好会对供应链决策产生影响,相关文献主要集中在三个方面:一方面是消费者低碳偏好对供应链决策的影响,例如:Du Shaofu等[11]通过构建考虑碳足迹和低碳偏好的需求函数,探究碳限额与交易系统中排放依赖企业生产决策的影响,通过建立生产优化模型制定最优决策。一些学者同时考虑了消费者低碳偏好与渠道偏好,探究了低碳供应链的决策问题[12-13]。另一方面学者关注闭环供应链中消费者对于再生产品的偏好。例如:Wang和Hazen[14]研究了再制造产品的成本、质量和绿色属性对消费者的影响,为再制造商和闭环供应链管理者制定管理政策和营销策略。陈晓红等[15]研究了基于消费者对再造品功能质量和环境质量支付差异下,政府的补贴行为和消费者偏好对供应链决策的影响。除此之外,还有一些学者对消费者质量偏好进行了研究,例如:刘云志和樊治平[16]分别分析了分散式和集中式供应链情形下供应商与损失规避型零售商的最优策,设计回购-质量成本分担的协调契约。温小琴和胡奇英[17]考虑了上游成员的机会成本和消费者在质量偏好的异质性,研究了中心化和分散化供应链在质量和数量上的最优产品策略。同样,消费者异质性偏好也会对扶贫供应链产生一定的影响,主要体现在消费者对与扶贫产品的偏好方面,但目前鲜有文献从智慧供应链供应链视角探究消费者对扶贫产品偏好,并分析其对于供应链上各部分的收益的影响。
规模不经济性指单位产品的生产成本随着产量的增加而增加。在现实中,囿于组织内外部资源和能力,绝大多数企业都或多或少存在规模不经济的情况[18-19]。许多学者关注规模不经济性对供应链的影响,例如:Ha等[20]在生产技术规模不经济效应下,探究零售商分别参与Cournot和Bertrand竞争的供应链纵向信息共享的激励机制。赵海霞等[21-22]研究了链与链数量竞争及制造商规模不经济情形下,两部定价合同选择的绩效改进条件、博弈均衡特征和局限性,就市场竞争强度、规模不经济参数对合同选择行为的影响进行了分析;并在此后,进一步研究探讨了市场竞争强度和规模不经济参数对于利润共享比例范围的影响。而聂佳佳等[23]在双渠道供应链中,讨论了规模不经济对制造商直销渠道选择的影响,研究了Bertrand 均衡下的渠道价格以及制造商和零售商最优利润。王先甲等[24]则在生产商规模不经济情形下研究了双渠道供应链协调策略选择问题,给出了集中决策下双渠道供应链的市场价格与整体利润,以及分散决策下批发价契约与收益共享契约的设计方法。显而易见,囿于技术和资源的限制,贫困地区农户的生产更是具有规模不经济的特征。而且,当前鲜有文献考虑扶贫供应链中农户生产规模不经济带来的影响,以及不经济生产成本被分担时给供应链所带来的变化。
综上所述,学者对于规模不经济的研究较为丰富,同时在研究消费者的偏好也有一定的探索,但是鲜有学者考虑在扶贫背景下农户规模不经济程度以及消费者扶贫偏好对于供应链决策的影响。
基于此,考虑到智慧供应链平台(扶贫馆)扶贫实践中,由于供应链各主体(例如合作社、批发商、智慧供应链平台扶贫馆、政府机构)之间的不同合作模式,会引起扶贫供应链结构的差异化。因此,本文构建了三种不同智慧供应链平台扶贫模式,分别从智慧供应链平台的智慧成本弹性系数、消费者扶贫偏好和农户生产规模不经济的程度等方面,探究对产品价格和平台收益、供应链上各主体的收益的影响。以期为农户、智慧供应链平台等模式选择提供依据,并为政府扶贫的补贴政策提供参考。
2 问题描述与假设
本文考虑了三种供应链模型,第一种农户+智慧供应链平台模式(模式A);第二种是在第一种模式的基础上加入批发商,与生产商和智慧供应链平台构成三级供应链(模式B);第三种则是考虑到增加了农村合作社的智慧供应链扶贫,贫困农户、合作社与智慧供应链平台形成的新型扶贫供应链(模式C),如图1所示:
图1 考虑消费者扶贫偏好的智慧供应链 结构示意图
为了更清楚进行研究分析,本文对模型进行如下假设:
假设1:智慧供应链平台与农户信息共享,其关于市场的信息是对称的,完全的。由于,在三种模型的终端都是通过平台将产品卖给消费者,因此,本文认为三种模型中的消费者对于扶贫产品的偏好和初始市场需求量是相同的,其初始市场需求量为d0,隐性市场需求量为d。
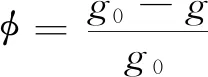
假设3:消费者对于市场上贫困户所产产品有一定的扶贫偏好k,k∈[0,1]。则在此情况下,市场的最终需求量为d0+φ(1-k)d,其中φ(1-k)为需求影响因子。因此,当农户的贫困程度越高,消费者对于扶贫产品越敏感,该产品的市场需求量越大。
假设4:产品的批发价格为w,产品的销售价格为pi(i=1,2,3),则需求函数qi(i=1,2,3)可以表示为:qi=d0+φ(1-k)d-pi。令H=d0+φ(1-k)d,则需求函数可表示为qi=H-pi。
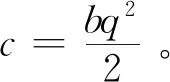
假设6:智慧供应链平台为生产商(农户、批发商以及合作社)提供销售服务,并向其收取一定的佣金,在生产商入驻平台时一般要缴纳一定的入驻费用,即为生产商的固定成本之一,为了计算便利,本文在不影响模型结论的前提下,忽略该固定成本,只计算其可变成本。
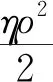
假设8:政府给予扶贫供应链一定的扶贫补贴,分别给予农户一次性补贴μmφ、合作社补贴μnφ,智慧供应链平台补贴μrφ。其中μ表示政府扶贫力度系数,φ代表扶贫量。
其中,决策变量为批发价格w,智慧供应链平台佣金ρ,产品的销售价格pi。
3 模型构建与分析
3.1 农户+智慧供应链平台模式
在此模式下,农户(生产商)和智慧供应链平台二者相互独立,只考虑自身利润最大化,不考虑对方及整体收益。根据Stackelberg博弈,智慧供应链平台作为博弈的主导者,农户为跟随者,决策顺序为:智慧供应链平台制定佣金ρ,农户根据佣金制定产品的价格p。此时,农户的利润函数、智慧供应链平台的利润函数、供应链利润函数可以分别表示为:
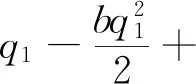
(1)
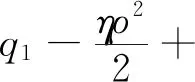
(2)
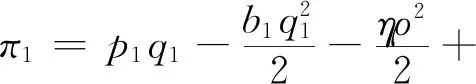
(3)
根据逆向归纳法,求解此模型的最优决策。
由(1)于∂2πm1/∂2p1=-(1+b)<0,所以πm1是关于p1的严格的凹函数,令∂πm1/∂p1=0,得,
(4)
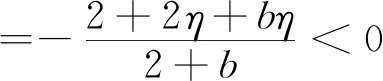
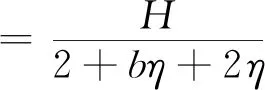
(5)
将(5)代(4),可求得最优价格,
(6)
将(5)、(6)分别代入农户、智慧供应链平台及供应链整体的利润函数,可求得模型的最优结果,即结论1。
结论1在农户+智慧供应链平台的模式中:
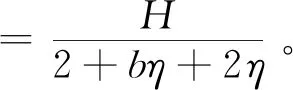
农户的最优利润为
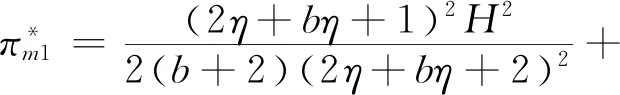
智慧供应链平台的最优利润为
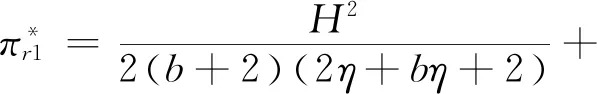
供应链的总利润为
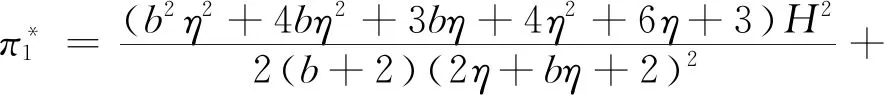
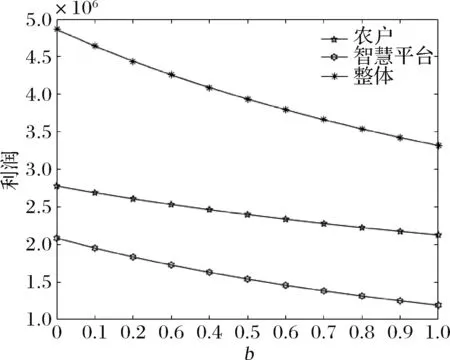
命题1在农户+智慧供应链平台合作模式下,农户的利润、智慧供应链平台以及供应链整体的利润均随农户规模不经济程度的增大而减小。
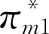
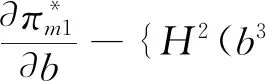
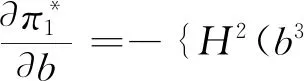
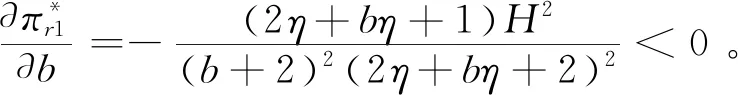
命题2在农户+智慧供应链平台合作模式下,农户、智慧供应链平台及供应链整体的利润随着农户贫困度的增大、随消费者对于扶贫敏感度的增大而增大。
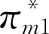
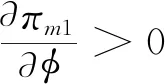
类似可证明其余结果均为正。
命题2的结论表明,当消费者对扶贫产品的敏感度一定时,随农户的贫困度的增加,产品的销售量会增加,导致供应链上各主体的收益都有所增加。当农户的贫困度一定时,随消费者对扶贫产品的敏感度的增加,产品的销售量也会增加,使得供应链上各方的收益都有所增加。因此,智慧供应链平台通过建立扶贫馆等,有效的刺激消费者,可以帮助农户获得更多的收益,更好的实现扶贫的目的。
3.2 农户+批发商+智慧供应链平台模式
很多贫困地区的农户受设备、能力、技术等的限制,不会选择直接与智慧供应链平台合作,而是将产品直接卖给批发商,由批发商和智慧供应链平台进行合作。假设扶贫背景下,农户会根据一般市场价格进行合理定价,但不会进行恶意要价,智慧供应链平台与批发商也愿为农户进行让步,使农户占主导,优先确定批发价。此时供应链成员的决策顺序为:农户决定批发价格w,批发商根据农户的决策制定产品价格p,智慧供应链平台根据产品价格决定佣金ρ。
此时,农户的利润函数、批发商的利润函数以平台的利润函数,可以分别表示为:
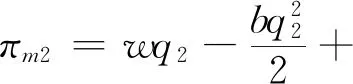
(7)
πn1=(p2-w-ρ-c1)q2
(8)
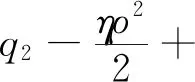
(9)

(10)
为保证供应链上各部分均处于收益状态,不失一般性,得相关条件:p2-w-ρ-c1>0。
根据逆向归纳法进行求解该模型的最优决策。
由(9)式,∂2πr2/∂2ρ=-η<0,所以πr2是关于ρ的严格的凹函数,根据∂πr2/∂ρ=0得,
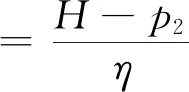
(11)
将(11)式代入(8),由于∂2πn1/∂2p2=-2(1+η)/η<0,所以πn1是关于p2的严格的凹函数,根据∂πn1/∂p2=0得,
(12)
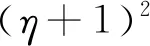
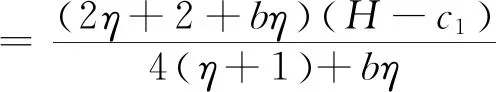
(13)
将(13)式代入(12)、(11)式可得最优价格和最优佣金,并进一步可得农户、批发商和智慧供应链平台的最优利润,即结论2。
结论2在农户+批发商+智慧供应链平台的模式中:
产品的最优批发价为
产品的最优价格为
智慧供应链平台的最优佣金为
农户的最优利润为
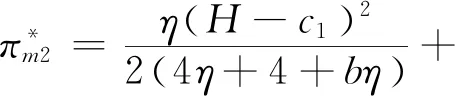
批发商的最优利润为
平台的最优利润为
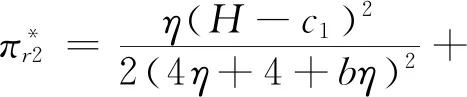
供应链的最优利润为
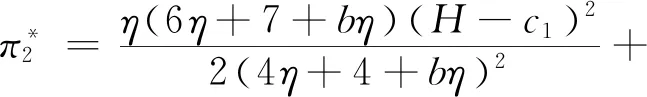
其中,农户的最优批发价格,产品的最优价格和智慧供应链平台的最优佣金应非负,故需H>c1。
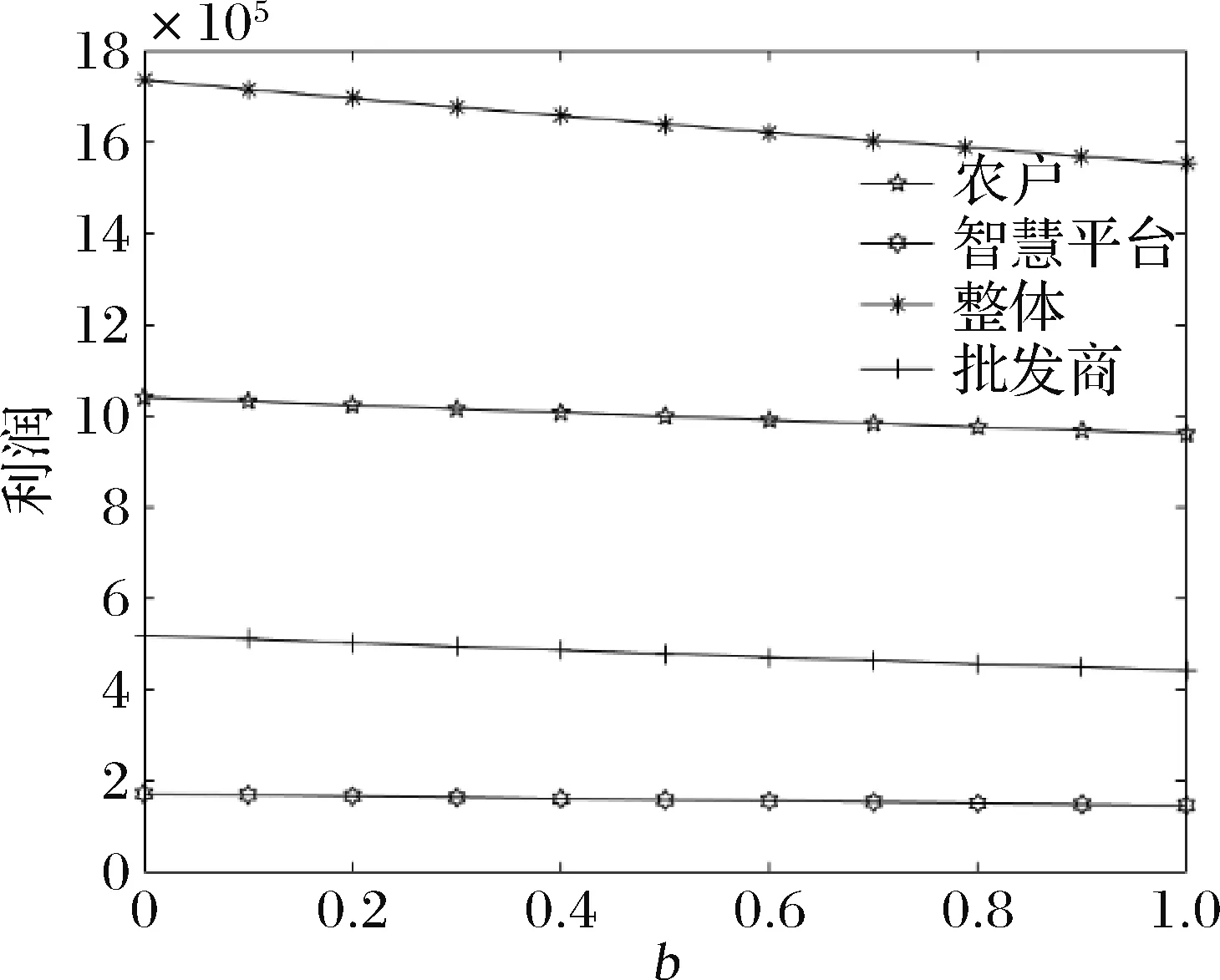
命题3在农户+批发商+智慧供应链平台模式下,农户、批发商、智慧供应链平台以及供应链整体的利润均随着农户规模不经济程度以及批发商的成本的增大而减小。
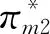
命题4在农户+批发商+智慧供应链平台合作模式下,农户、批发商、智慧供应链平台及供应链整体的利润随着农户贫困度的增大、消费者对于扶贫敏感度的增大而增大。
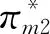
类似可证明其余结果均为正。
命题4的结论表明,在农户+批发商+智慧供应链平台合作模式下,当消费者扶贫产品的敏感度一定时,随农户的贫困度的增加,供应链上各方的收益均有所增加。当农户的贫困度一定时,随消费者对扶贫产品的敏感度的增加,供应链上各方的收益也均有所增加。因此,有效的刺激消费者,增强其对扶贫产品的敏感度对于扶贫供应链有重要意义。
3.3 农户+合作社+智慧供应链平台模式
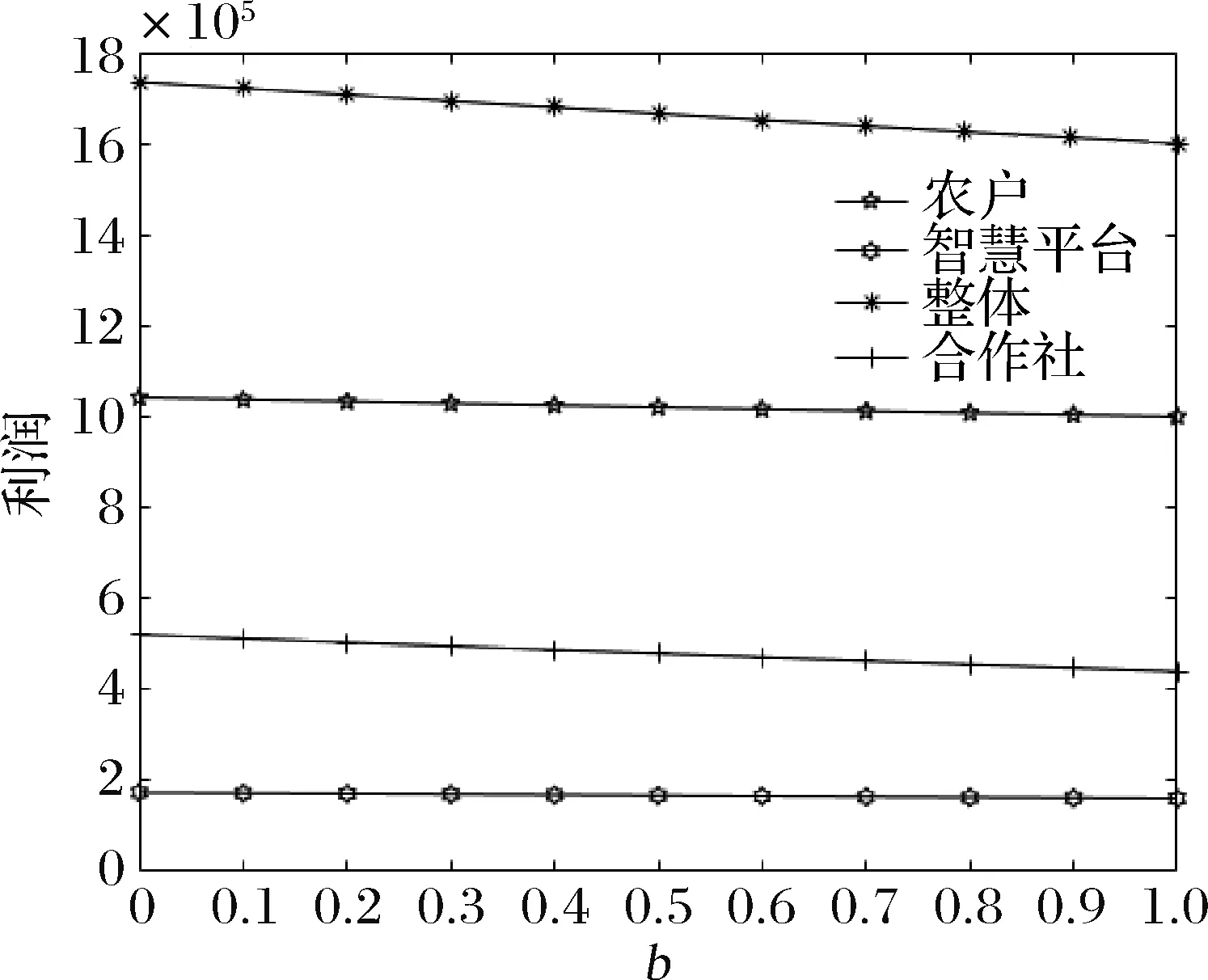
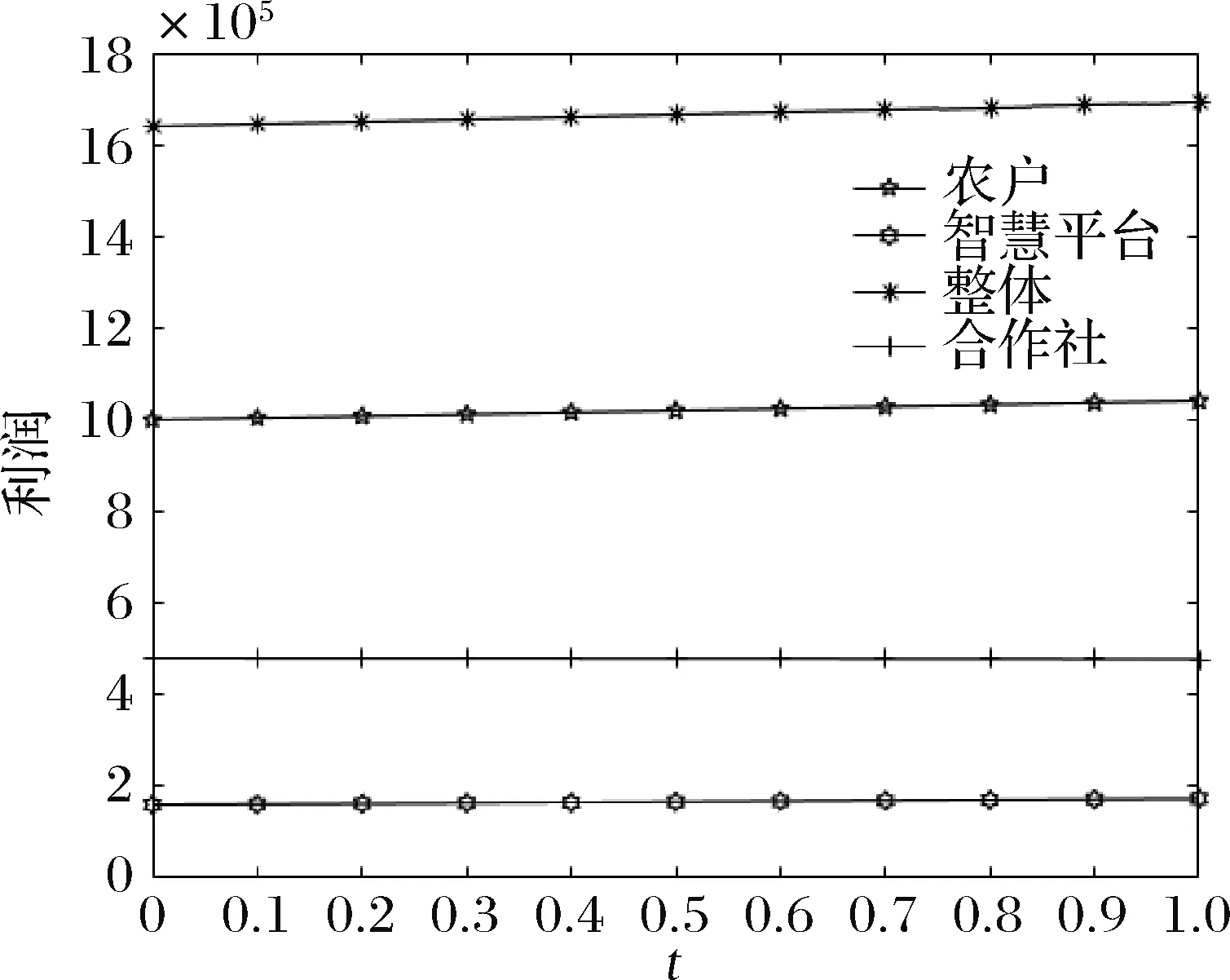
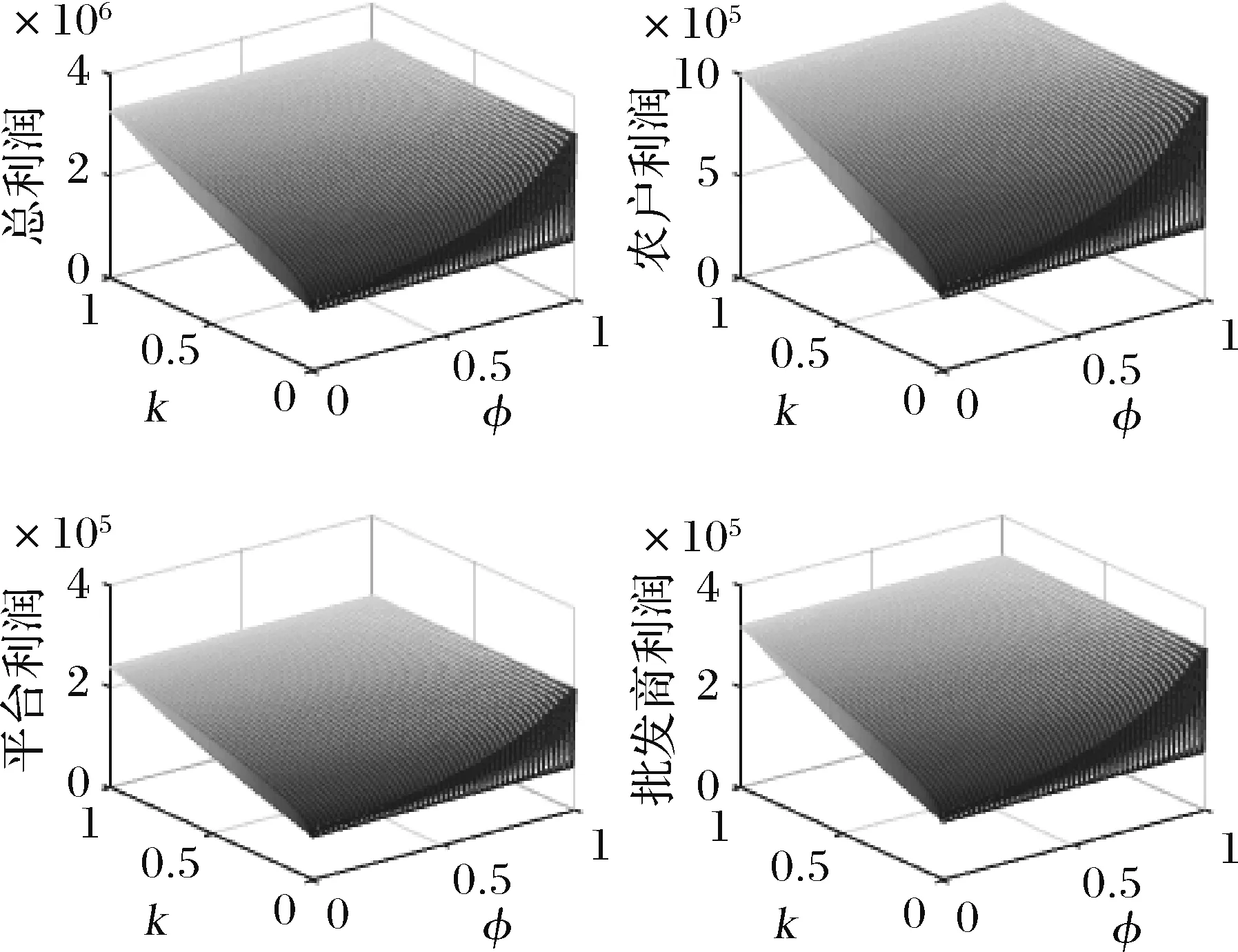
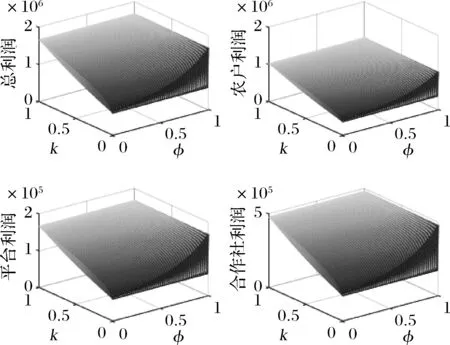
为改善农户的生产和销售状况,政府鼓励在贫困地区建立农业合作社。合作社通过为农户提供种子、化肥、农药及技术指导等方式为农户进行服务,协助分担规模不经济生产的成本,本文假设分担比例为t(0 此时,农户的利润函数、合作社的利润函数以及平台的利润函数,可以分别表示为: (14) (15) (16) (17) 相关条件:p3-w-ρ>0。由于政府此时给予合作社相应的补贴,合作社无偿分担农户成本,而不因为保持自身利益改变其决策。在此,用效用函数进行计算。 (18) Un2=(p3-w-ρ)q3+μn2φ (19) (20) 根据逆向归纳法进行求解模型的最优结果,求解过程同3.2节: 由(20)式,∂2Ur3/∂2ρ=-η<0,所以Ur3是关于ρ的严格的凹函数,根据∂Ur3/∂ρ=0得, (21) 将(21)代入(19),得∂2Un2/∂2p3=-2(1+η)/η<0,所以Un2是关于p3的严格凹函数。 根据∂Un3/∂p3=0得, (22) (23) 将(23)代入(22)、(21)式可得最优价格和最优佣金,并进一步可得农户、合作社、智慧供应链平台的最优利润,即结论3。 结论3在农户+合作社+智慧供应链平台的模式中: 产品的最优批发价为 产品的最优价格为 智慧供应链平台的最优佣金为 农户的最优利润为 合作社的最优利润为 智慧供应链平台的最优利润为 供应链的最优利润为 由0 命题5合作社为农户承担一定的规模不经济成本时,随合作社承担的比例的增加农户、智慧供应链平台及供应链整体利润均有所增加,但合作社的利润随其承担的成本的增加而有所减少。 命题6在农户+合作社+智慧供应链平台的模式下,农户、合作社、智慧供应链平台及供应链整体的利润均随农户规模不经济程度增大而减小。 命题7在农户+合作社+智慧供应链平台合作模式下,农户、合作社、智慧供应链平台及供应链整体的利润随农户贫困度的增大、消费者对于扶贫敏感度的增大而增大。 类似可证明其余结果均为正。 命题7的结论表明,在农户+合作社+智慧供应链平台合作模式下,农户的贫困度和消费者对扶贫产品的偏好均对供应链有正向的影响。智慧供应链平台类似于扶贫馆的建立,可以有效的刺激消费者,帮助农户及供应链整体获得更多的收益,更好的实现扶贫的目的。 证明 不考虑政府补贴的差异时,令 Δπm1=πm1-πm2 证明 不考虑政府补贴差异时,令: 由命题3、8、9可发现,在相同的政府补贴下,与农户直接与智慧供应链平台合作相比,批发商的加入会使供应链得收益重新分摊,农户和智慧供应链平台的收益都减小。因此,政府应给予“农户+批发商+智慧供应链平台”模式下的农户和智慧供应链平台更多的补贴,即(μm1<μm2), (μr1<μr2)。随批发商成本增大,两种模式的农户的收益差距和智慧供应链平台的收益差距都会逐渐增大,为达到扶贫的目的,政府给予农户的补贴μm2和给予智慧供应链平台的补贴μr2也需相应增大。 命题10政府补贴无差异下,农户+智慧供应链平台模式中供应链整体的利润大于农户+批发商+智慧供应链平台模式中供应链整体的利润。 证明 不考虑政府补贴差异时,令: Δπ1=π1-π2= 命题10的结论表明,在相同的政府补贴下,对比与农户+智慧供应链平台模式,批发商的加入,使供应链整体的收益再次被分摊,农户和智慧平台的收益减小。同时,批发商的运营增加了供应链整体的损耗,导致供应链整体收益也有所减小。因此,在批发商加入的模式下,政府需要同时加大对农户及智慧供应链平台的补贴,从而更好的实现扶贫的目的。 命题11政府补贴无差异下,农户+智慧供应链平台模式中农户的收益高于农户+合作社+智慧供应链平台模式中农户的收益,二者的收益差会随合作社成本分担系数t的增大而减小。 证明不考虑政府补贴的差异时,令 命题12政府补贴无差异下,农户+智慧供应链平台模式中智慧供应链平台的收益高于农户+合作社+智慧供应链平台模式中农户的收益,两者的收益差会随合作社成本分担系数t的增大而减小。 证明 不考虑政府补贴的差异时,令 通过命题5、11、12不难发现,在相同的政府补贴下,与农户直接和平台合作相比,合作社的加入也会使得农户和智慧供应链平台的收益都受到一定程度的侵占。此时,政府应给予该模式下的农户和智慧供应链平台更多的补贴,即(μm1<μm3), (μr1<μr3)。合作社应尽可能多的为农户分担生产成本,使得农户和智慧供应链平台的收益均有所增加,此时,政府给与农户和智慧供应链平台的补贴(μm3,μr3)可随之减小。但随着所分担的成本的增加合作社的收益会减少,政府给予合作社的补贴(μn2)应随之增加,从而更好的实现扶贫的目的的同时保障合作社的收益。 命题13农户+智慧供应链平台模式中供应链整体的利润大于农户+合作社+智慧供应链平台模式中供应链整体的利润。 证明 不考虑政府补贴的差异时,令: Δπ2=π1-π3 命题13的结论表明,在相同的政府补贴下,对比与农户+智慧供应链平台模式,批发商的加入,使供应链整体的收益再次被分摊,农户和智慧平台的收益减小。同时,批发商的运营增加了供应链整体的损耗,导致供应链整体收益也有所减小。因此,在合作社加入的模式下,政府需要同时加大对农户及智慧供应链平台的补贴,从而更好的实现扶贫的目的。 为了进一步对模型进行分析,验证所得结果,本节对上述模型进行数值分析,模型的基本参数赋值如下: 假设山东省某以种植草莓为特色的贫困县存以上三种供应链扶贫模式,供应链中潜在的市场需求量H=5000,其中,农户的贫困度φ=0.5,消费者对于扶贫产品的敏感度k=0.5,农户的规模不经济系数b=0.5,智慧供应链平台的智慧成本的弹性系数η=0.5,批发商出售单位草莓的成本(包含运输、储存、损耗等)c1=2,合作社为农户分担的成本的比例t=0.5,政府不给予供应链任何补贴。 规模不经济程度对农户的生产会产生直接的影响,进而对供应链上各部分的收益发生改变。合作社为农户所分担的规模不经济成本的改变,又会对其自身产生一定的影响。由命题1、3、5、6、11、12、13,可以得到图2~5。图2~5分别反映了了规模不经济程度、合作社成本分担系数对于不同模式下的供应链上各主体的利润的影响。 图2 规模不经济对模式A各主体利润的影响 图3 规模不经济对模式B各主体利润的影响 图4 规模不经济对模式C各主体利润的影响 图5 分担成本系数对模式C各主体利润的影响 (1)规模不经济程度对各主体的影响。 图2~4反映了合作社分担成本t=0.5时,不同模式下当规模不经济程度b在(0,1)范围内变化,对供应链各部分的利润的影响。 从图2、3、4可以看出,在三种模式下,供应链各主体的利润均随农户规模不经济程度的增大而减小。由于农户生产的规模不经济程度增大,其单位生产成本增加,使产品的价格提高,需求量减少,从而导致农户和智慧供应链平台的利润均越来越小。批发商及合作社的利润均小于农户利润,智慧供应链平台的利润在供应链中处于最低。因此,政府应该给予智慧供应链平台更多的补贴,鼓励他们为农户服务。 当合作社帮农户分担生产成本后,与合作社合作的农户的利润高于与批发商合作的农户的利润,而两种模式下智慧平台的利润是基本相同的,合作社与批发商的利润也基本相同。因此,政府应积极鼓励合作社的建立,使他们在帮助农户提高生产技术水平的同时提高农户的收益,从而更好的实现扶贫。 (2)分担成本系数对供应链上各主体的影响 从图5可以看出,在农户与合作社合作的模式下,随合作社分担的生产成本的增加,农户、平台和供应链整体的利润均有所增加,合作社的利润略有减少。因为农户成本被分担促使产品价格降低,从而导致需求量的增加,使得利润的增加。对合作社而言,需求量增加带来的收益未能抵消其为农户承担成本的付出,因此其利润减小。 比较图2、3、4、5可以发现,农户直接与智慧供应链平台合作社模式下,农户和智慧供应链平台获利最多。因为减少了中间环节,降低了产品价格和供应链整体的损耗,对消费者和农户均有利。但是在现实的贫困地区,尤其是对年迈的农户,其的知识技能水平的不足及当地的硬件设施的配置(如电脑)的不完善,使得农户很难做到直接与智慧供应链平台合作。因此,绝大部分农户都会选择与批发商或合作社合作。现阶段农户加入合作社是更好的选择,在获得合作社的技术指导的同时,可获得更多的收益,因此政府需要激励合作社的建立。从长远来看,政府需要通过合作社对农户提供指导,帮助农户提高生产技术水平与科学文化素养,并完善硬件设施的配备,最终实现农户与智慧供应链平台自主合作。 由于平台提供的大数据预测、智慧营销服务、物流服务等服务所投入的资金不同,对于不同模式供应链各主体部分的利润影响也有所不同。图6~8反映了不同模式下智慧供应链平台的成本的弹性系数为η在(0,1)范围内,对供应链各部分的利润的影响。 图6 成本的弹性系数对模式A各主体利润的影响 图7 成本的弹性系数对模式B各主体利润的影响 图8 成本的弹性系数对模式C各主体利润的影响 从图6、7、8可以看出,在三种模式中,农户、批发商、合作社及供应链整体利润均随着智慧平台智慧成本的弹性系数的增大而增加。成本的弹性系数越大,即智慧供应链平台进行大数据预测、智慧营销等服务所投入的资金越多,会使得消费者的需求量增大,农户、批发商及合作社的利润增大。农户直接与智慧供应链平台合作时,智慧平台的利润随成本系数的增加而减少,是由于其智慧化程度的增加导致成本的大幅增加,而需求量的增加并不能弥补其付出的成本,进而导致利益的减少。当批发商、合作社加入到供应链中时,智慧供应链平台的利润随智慧成本弹性系数的增大先增大后趋于平缓,对此进一步进行数值分析,如下: 由表1可以看出,两种模式下的智慧供应链平台的利润均随智慧成本弹性系数的增大先增大后减小,并分别在η=0.8和η=0.9时取得最大值。是因为当其智慧服务成本过高时,智慧供应链平台将处于劣势,需求量增大带来的收益将不能填补其成本的损耗,其利润会随着成本的增加逐渐减小。联系图5、6、7说明两种模式下,智慧供应链平台应将成本的弹性系数进行合理控制,可使得智慧供应链平台自身获得最大利润的同时,供应链其他各主体也可以获得较高的收益。 表1 智慧成本的弹性系数对B、C两种模式中智慧供应链平台利润的影响 由于智慧供应链平台的收益在供应链中处于相对劣势的状态,政府应给予智慧供应链平台更多的补贴,在保证智慧供应链平台的收益的同时促进其服务的智慧化程度的提高,从而增加农户收益,实现扶贫的目的。 由命题3、6、10,分别得到图9~11。图9~11反映了不同模式下,农户的贫困程度0<φ<1时与消费者的扶贫敏感度0 图9 农户的贫困程度与消费者的扶贫敏感度对模式A各主体利润的联合作用 图10 农户的贫困程度与消费者的扶贫敏感度对模式B各主体利润的联合作用 图11 农户的贫困程度与消费者的扶贫敏感度对模式C各主体利润的联合作用 从图9、10、11可以看出,在三种模式下,随着农户的贫困程度的增加,供应链各主体及供应链整体的利润均随着农户的贫困程度的增加而增加,随着消费者对扶贫产品的敏感度的增加而增加。由于农户贫困程度越高,越容易激发消费者的情感,从而拉动需求,促进供应链各主体利润的增加。 不难看出,当0<φ<0.5时,随着农户贫困程度的增加,供应链上各个主体及供应链整体的利润虽均有所增加,但增速较为缓慢;当0.5<φ<1时,随着农户贫困程度的增加,供应链上各个主体及供应链整体的利润有较大的提高。原因在于,当农户的贫困度较低时,消费者虽然会产生一定的同情心理,但不会对其消费产生较大的影响;但当农户的贫困程度超过消费者心中某一限度,消费者会在消费过程中融入更多的个人情感,促使产品销量增加。比如阿里巴巴集团与共青团广西区委共同签署《阿里巴巴广西青年“青春建功”电商扶贫计划合作备忘录》,为广西33个国家级贫困县宣传,利用农村淘宝联合聚划算发起的“寻味广西”抢购活动,自8月15日上线即遭疯抢,3天时间内卖出超33万件,成交额破800万。因此,智慧扶贫平台的建立,可以有效的使消费者了解到贫困地区的农户及当地的现状,从而拉动需求,实现扶贫的目的。 针对农户生产具有规模不经济性特点,本文立足于考虑消费者偏好的扶贫供应链的分散式决策问题,分别构建了本文分别构建了“农户+智慧供应链平台”、“农户+批发商+智慧供应链平台”、“农户+合作社+智慧供应链平台”三种不同供应链扶贫模式,通过Stackelberg博弈,分析并比较了不同模式下智慧扶贫供应链的分散式决策及政府的补贴策略,最后借助数值分析对模型进行分析。研究表明:(1)农户直接与智慧平台合作模式下,农户和智慧平台会获得更多的收益。由于贫困地区的经济与技术发展水平的限制,大部分农户会选择与批发商或合作社合作,而随着合作社为农户承担的规模经济不经济的成本的增加,农户的利润会逐渐增加,因此这种模式可以更好地满足扶贫的目的。(2)农户的贫困程度及消费者对于扶贫产品的偏好对产品的需求均会产生正向影响,使得三种模式下供应链各主体及供应链整体的利益有所增加。(3)现阶段,政府应加大力度激励各地合作社的建设,引导合作社为农户分担一定的生产成本并对其进行生产技术及科学技术的指导,帮助农户提高生产技术水平并逐步发展可以直接与智慧供应链平台合作。同时,政府可以采取多种方式对智慧供应链平台进行激励,使其积极投入到智慧扶贫中来。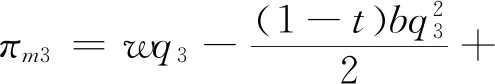
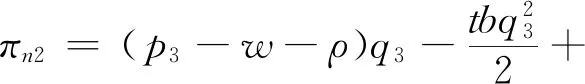
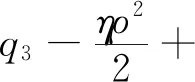
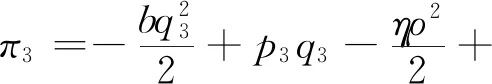
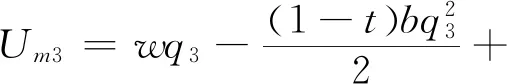
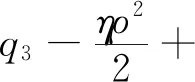
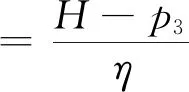
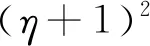
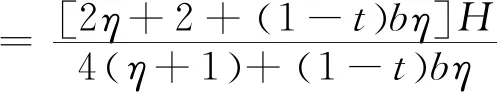
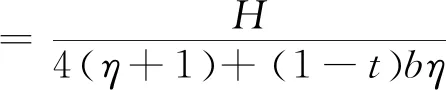
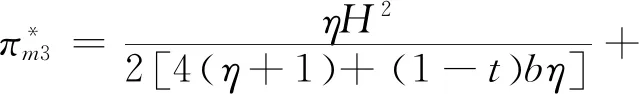
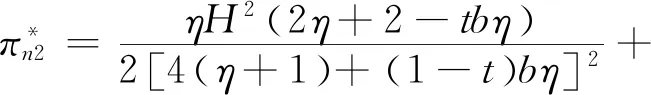
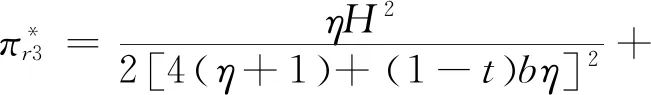
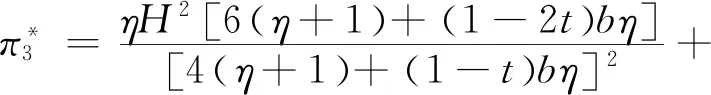
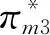
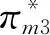
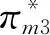
4 模型间比较
4.1 农户+智慧供应链平台模型与农户+批发商+智慧供应链平台模型比较
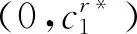
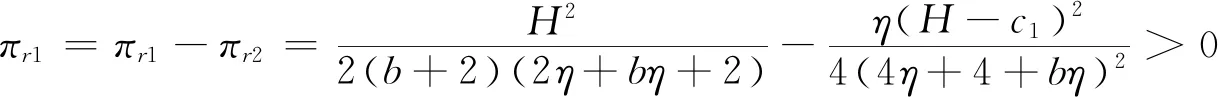
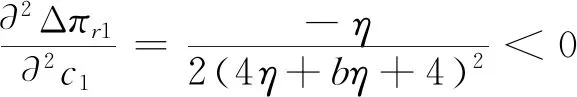
4.2 农户+智慧供应链平台模型与农户+合作社+智慧供应链平台模型比较
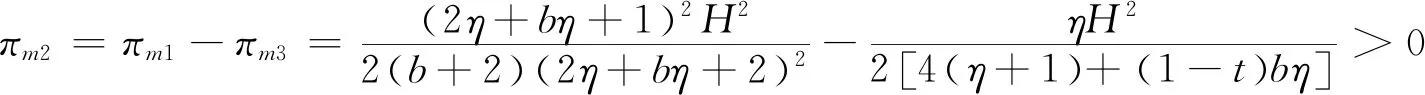
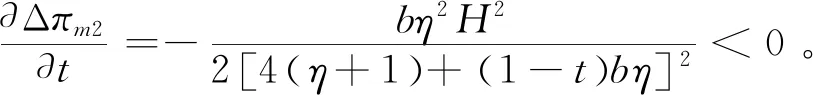
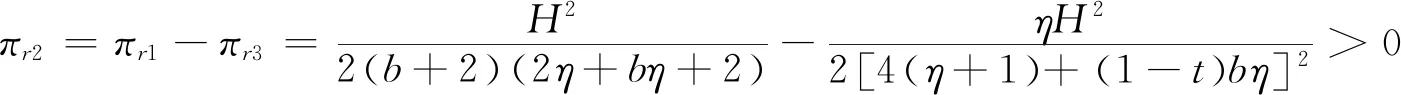
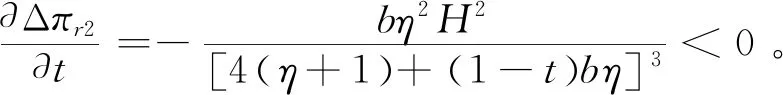
5 数值分析
5.1 规模不经济程度及合作社分担成本的系数对相关参数的影响
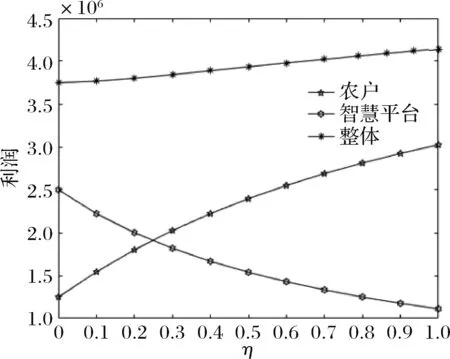
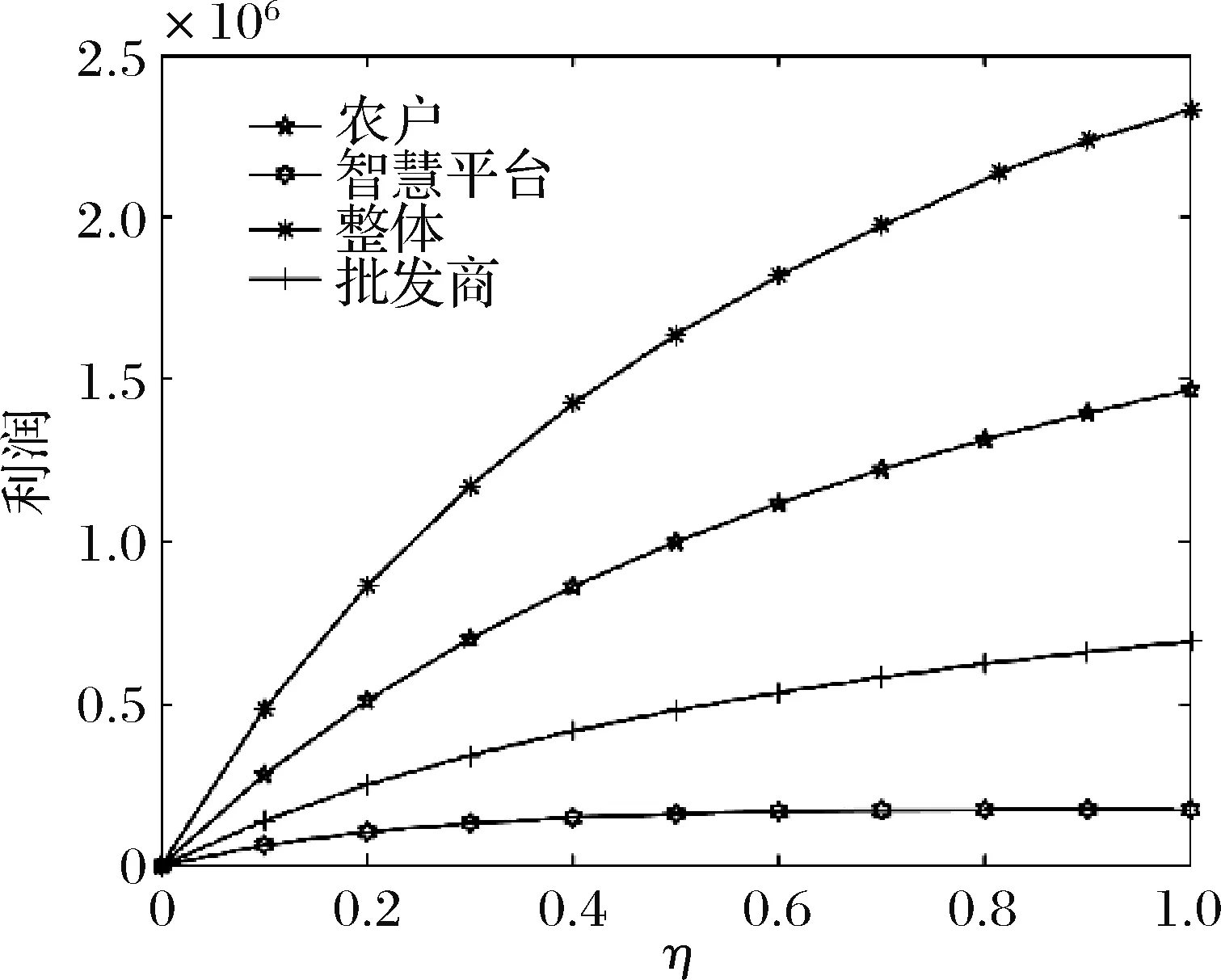
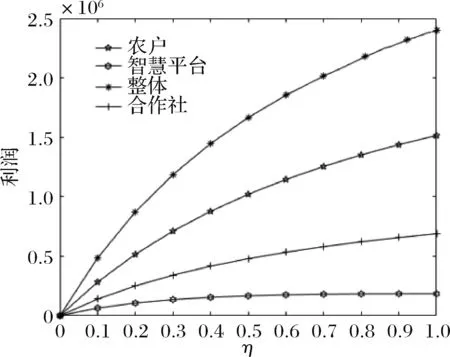
5.2 智慧供应链平台单位成本的弹性系数对相关参数的影响

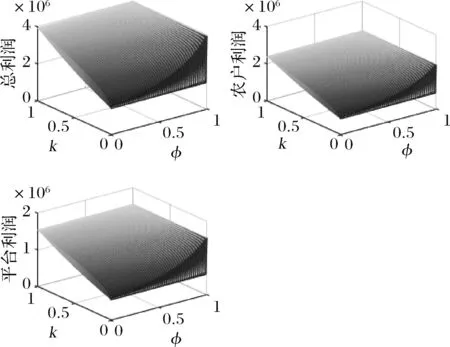
5.3 农户的贫困程度与消费者的扶贫敏感度对相关主体利润的联合作用
6 结语

