公共服务平台下虚拟联盟成员选择机制及联盟企业间协同制造问题研究

刘捷先，张 晨

(1.合肥工业大学管理学院，安徽 合肥 230009；2.铜陵学院会计学院，安徽 铜陵 244061)

1 引言

近年来，随着中国制造2025等国家制造战略的积极推进，制造企业开始探索如何利用以工业互联网、工业机器人和工业大数据为核心的智能制造技术实现企业的转型升级。目前，工业4.0基础性工程的不断完善，促进了信息物理系统(CPS)的跨越式发展，兼具虚拟化、网络化、智能化等特征的智能制造体系已经成为可能。网络化协同制造模式下，价值网络的价值创造活动将被重新定义，价值创新链条将被重新塑造。新型价值网络环境下，传统供应链和产业链将被重组，各类不同层级的制造活动和合作方式将会涌现，以敏捷制造、虚拟制造和协同制造为代表的新型制造模式将会是新型价值网络价值创造的主要组织模式。航空制造业在这方面已经有了较为丰富的实践。世界一流航空公司如波音、空客、庞巴迪在民航客机的制造实践中实现了具备网络化、协同化特征的虚拟制造模式。在波音787民航客机的全球化制造过程中，波音公司通过虚拟装配模型集成了日本的大型重工、俄罗斯的设计中心以及波音的埃弗雷特工厂等全球范围内的设计制造资源，支持了波音787客机的创新设计、虚拟装配、校对测试等业务流程集成。

虚拟制造联盟作为协同制造的主要主体，面对个性化需求环境下激烈地的市场竞争，要求其具备自适应演化、闭环式反馈、协同式优化的特征。公共服务平台作为服务型协同制造模式的载体，其目的在于利用物联网、工业互联网、工业大数据等新兴信息技术实现全球范围内碎片化制造资源的标准化、组件化、服务化集成，主动将顾客纳入产品制造服务过程、挖掘并培育客户需求。当前，我国政府部门及工业界都开始积极探索制造服务化背景下公共服务平台的构建，诸如吉林省制造业与服务业融合公共服务平台、紫光工业云引擎平台UNIPower等智能制造公共服务平台相继涌现。在虚拟协同制造理论研究方面，国内外针对虚拟制造联盟方面的研究主要集中在虚拟制造联盟伙伴选择、虚拟制造联盟利益分配机制以及虚拟联盟知识共享机制等方面。Camarinha-Matos和Afsarmanesh[1]指出虚拟联盟是指在网络化环境下独立且异地分布的企业为了抓住商务机遇而形成的临时性企业联盟，在虚拟联盟内的企业可以共享核心技术和资源。Chen等[2]和Crispim和Jorge[3]从多属性决策的角度分析了各种影响虚拟联盟伙伴的选择的有形和无形的因素，给出了模糊数据情形下的联盟伙伴选择机制。Wang等[4]提出了一种混合DEA和灰色理论模型的评价方法，用于解决汽车制造企业虚拟联盟的伙伴选择问题。戴建华和薛恒新[5]基于多人合作理论中的 Shapley

值理论, 研究了动态联盟中伙伴成员的利益分配问题。卢纪华和潘德惠[6]研究了技术开发项目过程中虚拟企业的利益分配问题, 构建了基于博弈论理论的虚拟企业利益分配模型，以确定合作企业在项目实施中的利益分配系数。Chiu等[7]从社会资本和社会认知的角度定义了虚拟社区/企业中的知识共享行为。Niki和Sockalingam[8]研究了具有复杂内联关系的虚拟联盟中信任和冲突现象，并给出了该联盟的知识共享实施框架。Hsu[9]从信任、自我效能、产出期望三者之间的关系出发，诠释了虚拟联盟中存在的知识共享行为。

不同于以往虚拟制造联盟方面的研究，本文旨在实现虚拟制造联盟战略层面和运营层面的有机融合，即不再局限于单独研究战略层面的伙伴选择问题以及运营层面的协同生产问题，而是把这两个问题当作一个整体联合考虑。因此，本文提出了虚拟联盟成员选择和企业成员之间协作生产的联合优化模型，该模型能够实现联盟企业选择、顾客订单分配以及订单排序生产等三个层级的协同决策。本文的主要创新点可概括如下：

(1)提出了虚拟制造联盟背景下联盟企业选择和联盟企业间协同制造模型，将原本独立的联盟成员选择问题和企业制造联盟协同生产问题有机融合，能够更为全面地提升虚拟联盟的制造效率。

(2)提出了考虑机器老化效应情形下单一联盟企业的订单排序生产最优化方面的性质，给出了单一联盟企业的订单最优化生产方法。在此基础上提出了多个联盟企业间的订单分配原则，给出了有关于联盟成员选择的性质引理。

(3)设计了二维离散编码策略以及离散数种子代产生规则，开发了离散树种算法，使得用于求解连续优化问题的树种算法能够求解本文提出的离散优化问题，并结合前述提出的性质引理，提出了个体的适应度计算方法。

2 虚拟联盟成员选择及联盟企业间协同制造问题描述

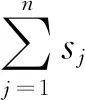
为了最大化所获利润，平台需要进行三层决策，第一层决策集中在如何选择合理的制造企业组建制造联盟，第二层决策集中在如何将订单分配到制造联盟的各个制造企业处，第三层决策集中在如何在各个制造企业处对已分配订单进行排序生产。为了更为清楚地表达这三层决策之间的逻辑关系，本文将这一系列决策过程以简图的形式表达如下图1：

图1 虚拟联盟公共服务平台三层决策示意图

3 虚拟联盟成员选择及联盟企业间协同制造问题分析

遵循自底向上的研究路线，本文从第三层决策过程着手，假设第一和第二层决策过程已经完成，即虚拟联盟业已建立并且分配到各个制造商处的订单集合也以确定。不失一般性，假设制造企业mi为虚拟联盟中的一员，并且分配到该企业的订单总数记为ni，相应的订单集合记为Oi={Oij|j=1…ni}。针对单个制造企业处的订单排序问题，本文给出了以下与第三层决策相关的性质引理。

引理1. 针对单个制造企业处的订单排序问题，该制造企业最后一个订单的完工时间记做Ci，可表示为：

(1)

证明：该定理可用数学归纳法进行证明。当只有一个订单，即j=1时，制造企业mi处最后一个订单的完工时间为：

Ci=t0+pij+at0=(1+a)t0+pi1

显然当j=1时，公式(1)成立。假设当订单数为k，即j=k时，公式(1)成立，则有

在此情况下，当j=k+1时，制造企业mi处最后一个订单的完工时间为：

显然可见，当j=k+1时，公式(1)成立。因此，公式(1)对于j=ni同样成立。由此，该引理得证。

推论1.针对单个制造企业处的订单排序问题，该制造企业总的制造成本可表达为：

证明：该引理证明可参见Hardy等[11]。

引理 3. 针对单个制造企业处的订单排序问题，当订单按照其基本处理时间从大到小排序加工时，该企业的总制造成本最小。

根据引理3，我们设计了算法1以最优化单个制造企业处的订单排序。算法1可描述如下：

算法1步骤1.将分配到制造企业mi处的ni个订单按照其基本处理时间从大到小进行排序步骤2.按照上述排序依次加工各个订单,根据引理1计算最后一个订单的完工时间Ci步骤3.根据公式∑nij=1sj-gi-fiCi计算制造企业mi处获得的利润

引理4. 在所提问题的一个最优解中，各个制造企业处最后一个订单的完工时间与其单位时间加工成本的数值单调相反，即若fs1≤…fsi…≤fsSM，那么Cs1≥…Csi…≥CsSM。

证明：该引理与引理3证明相似，此处省略。

关于第一层决策，将制造企业集合MP中任意两个制造企业分别记为mi1和mi2，我们给出了如下引理。

引理5. 在选择制造企业组建虚拟联盟时，若有两个制造企业满足如下关系：

那么，制造企业mi1的优先权要高于制造企业mi2。

证明：该引理显然易见，此处省略。

传统粉彩人物是现代粉彩人物的根，现代粉彩人物瓷画正是建立在传统粉彩人物瓷画的基础之上，逐渐形成。而传统粉彩人物瓷画源流有两大类，其一是民国时期的新粉彩人物，其二则是清代的古典粉彩人物。

在本节中，我们针对虚拟联盟企业选择、顾客订单分配，订单排序生产等三个层面的决策过程，给出了各个层面决策的引理性质，根据引理给出了单个制造企业处的订单最优排序。为了进一步解决虚拟联盟企业之间的协同制造问题，本文设计了嵌入算法1的离散树种算法。树种算法中的二维编码机制用于联盟企业选择和分配订单到各个制造企业处。算法1用于各个制造企业处的订单排序。

4 离散树种算法

考虑到虚拟联盟制造企业间协同优化问题的复杂性，本文提出了嵌入算法1的离散树种算法用于求解该问题。在本节，我们将简要介绍基本的树种算法，给出离散树种算法的编码策略，并提出子代种子的生成规则。

4.1 树种算法简介

树种算法(Tree-Seed algorithm，TSA)最先由Kiran[12]提出，用于求解连续优化问题。该算法主要模拟自然界中树木和其种子之间的关系，树木通过掉落的种子来繁衍生出新的树木，每棵树上种子散落的位置决定了下一代树木的所在位置。树木所在的地表空间可以看成连续优化问题的解空间，树木所在的位置可以看成解空间中的解。树木与种子之间的不断循环繁衍可以看作解空间中的初始解不断迭代优化。算法的基本步骤如下所示：

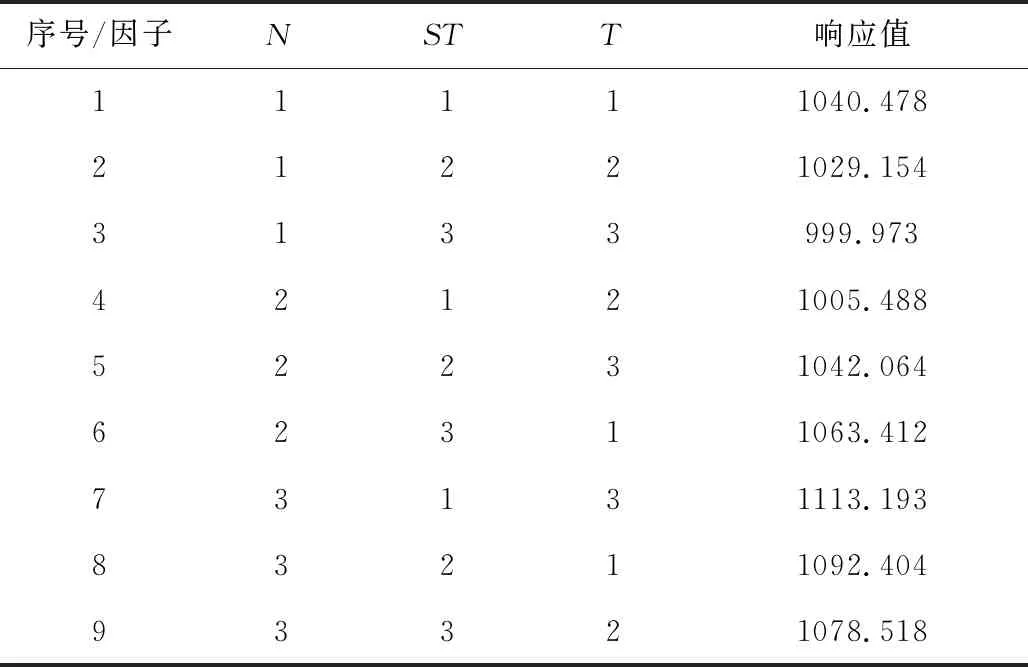
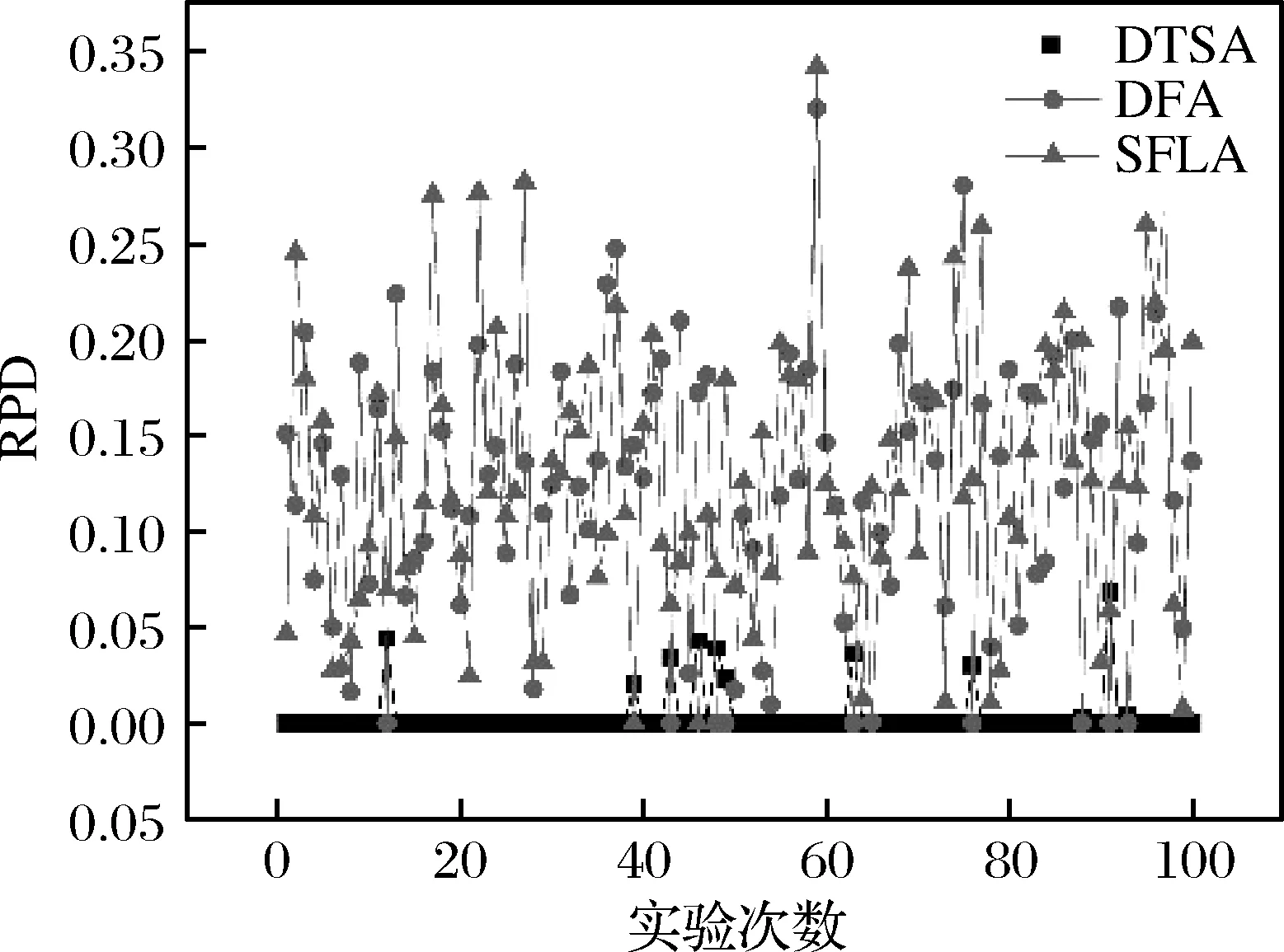
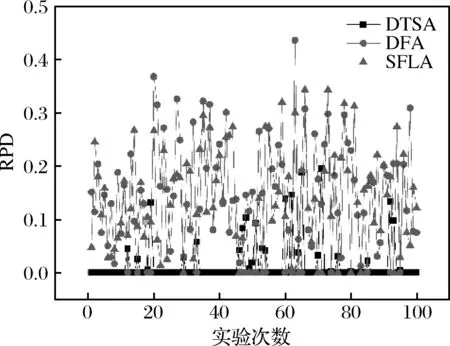
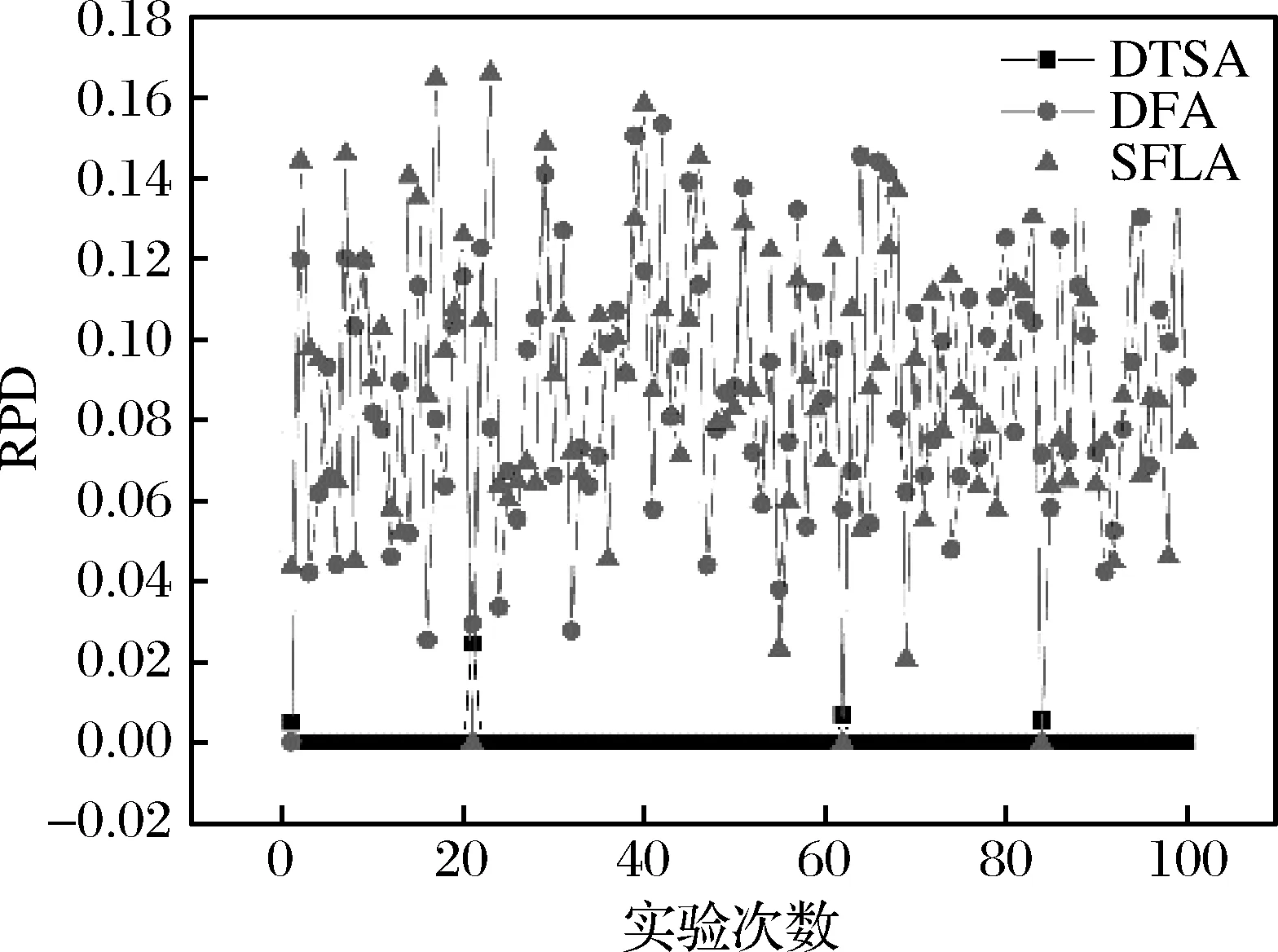
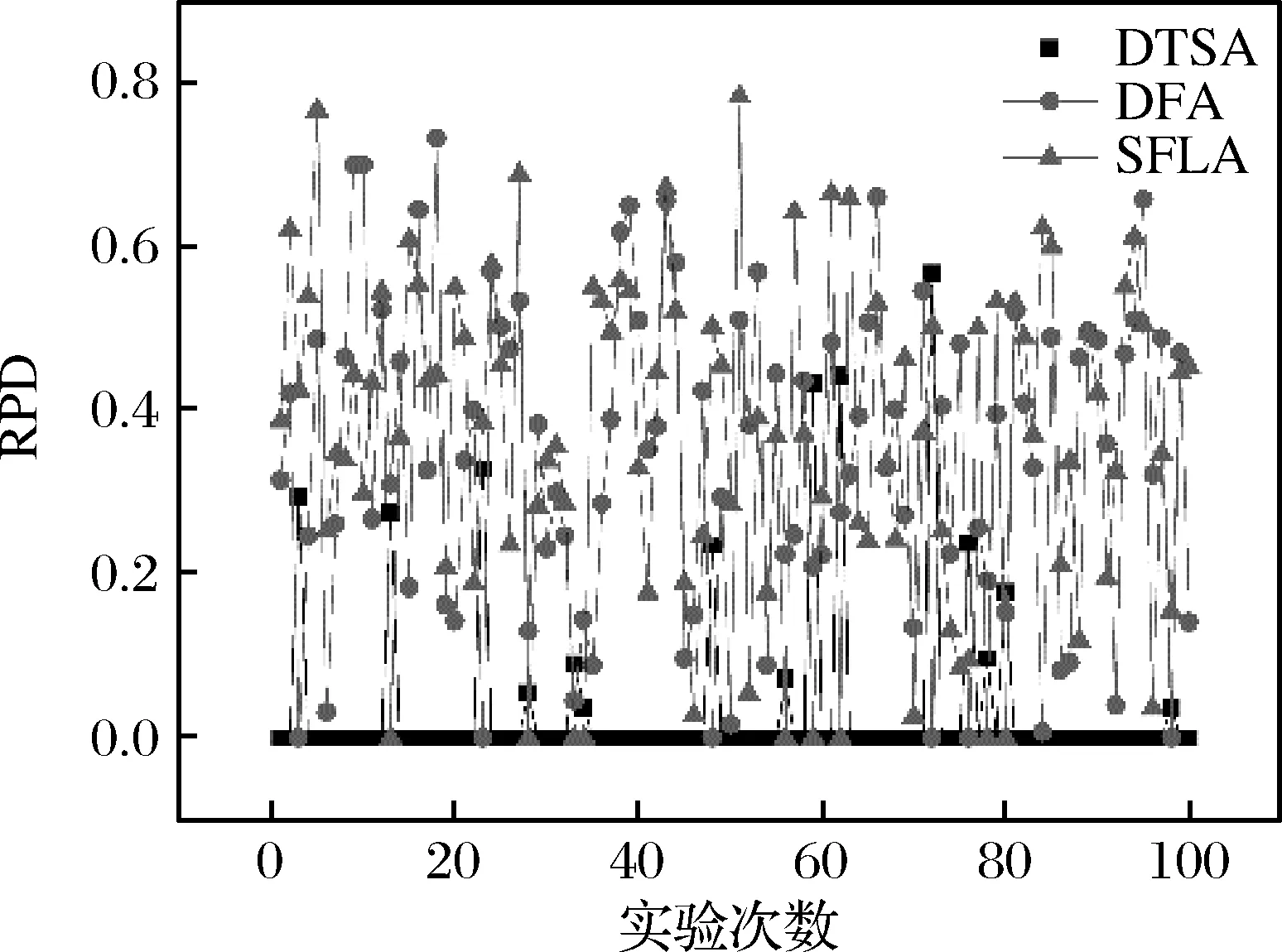
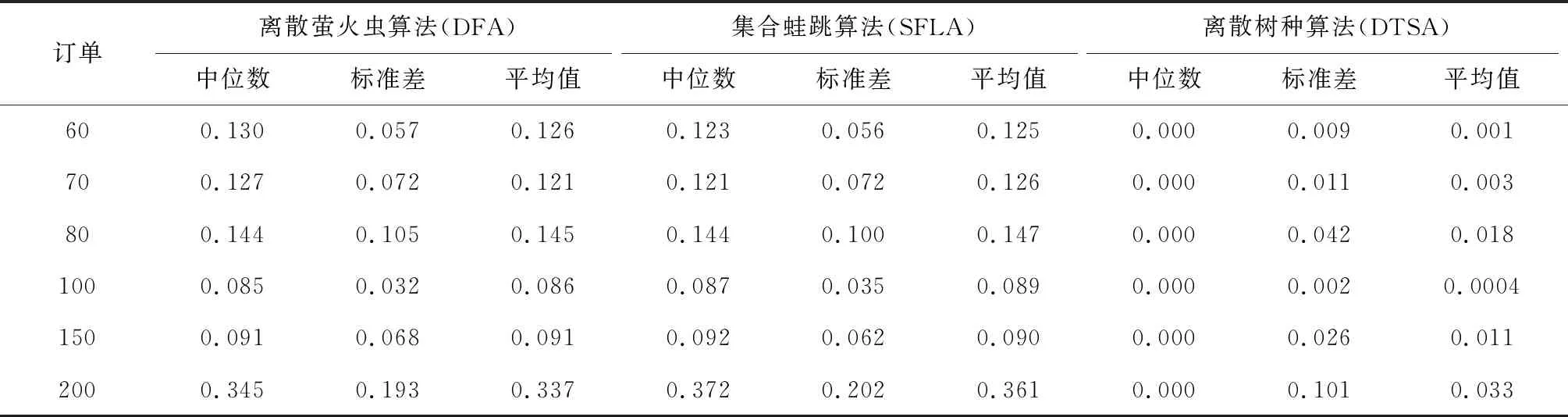
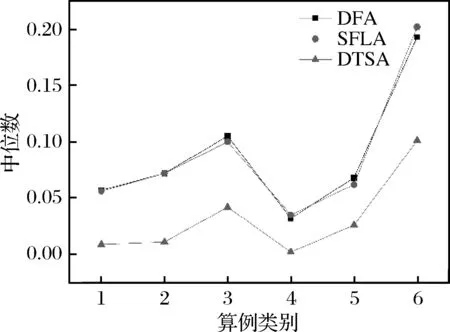
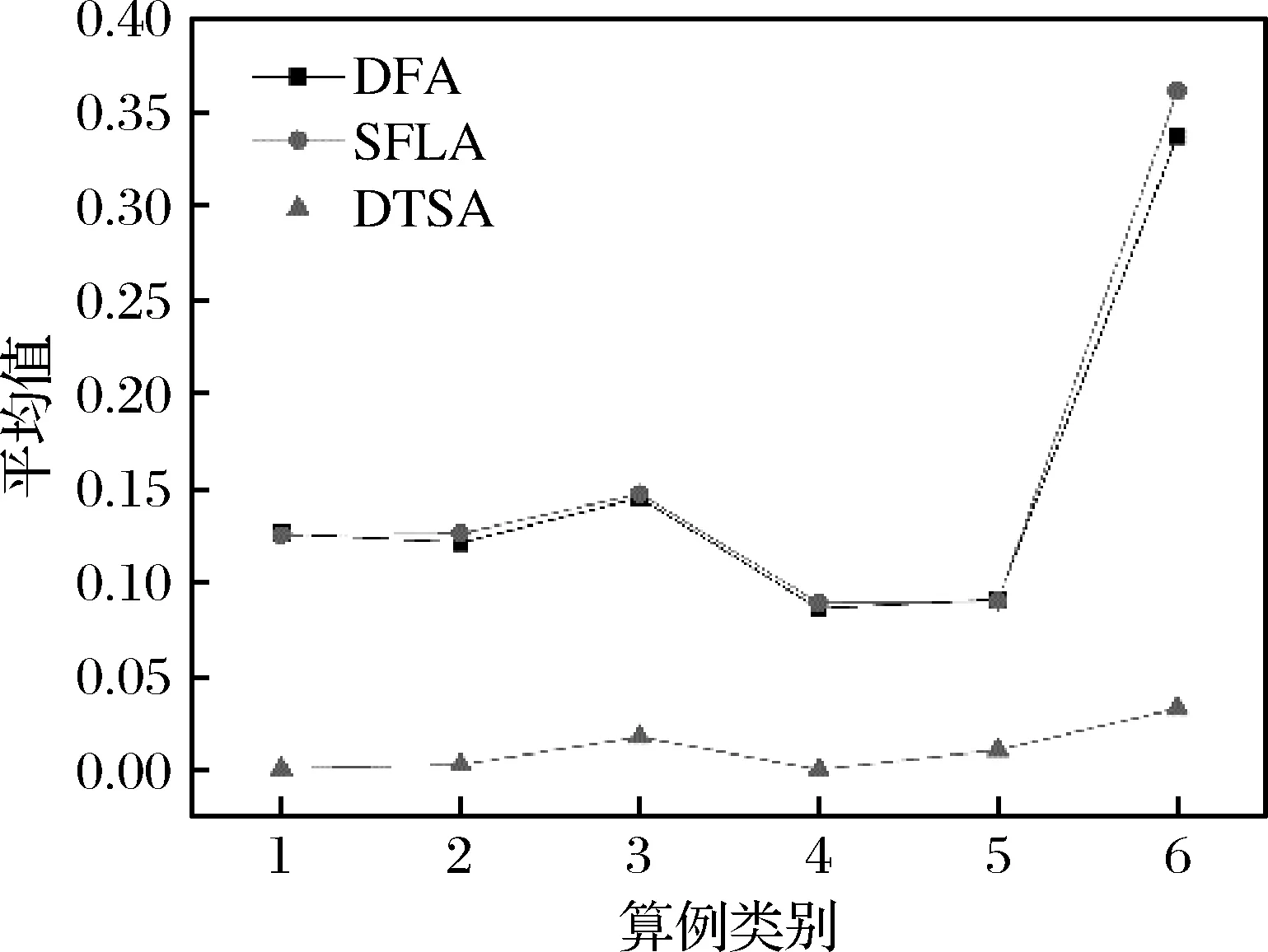
树种算法步骤1.初始化算法参数,包括种群数目N、搜索趋势控制参数ST、问题维度D、算法迭代终止时间T。步骤2.在D维解空间初始化N棵树木的初始位置,记作POP0 =T10 …Tl0 …TN0 ,其中Tl0 表示初始种群中的第l棵树木,Tl0 =Tl10 …Tld0 …TlD0 。步骤3.依次计算每棵树木的适应度值,记作Fit0 =F10 …Fl0 …FN0 ,其中Fl0 表示初始种群中的第l棵树木的适应度值。记录当前最好解为B并令当前迭代次数it=1。步骤4.当前考虑的树木序号l=1。步骤5.随机设置第l棵树木的种子的数目SN∈10%N,25%N 。步骤6.令当前考虑的种子序号为sn=1。步骤7.令d=1。步骤8.若rand

4.2 二维离散编码策略

从基本树种算法的简介可以看出该算法主要用于求解连续优化问题，然而本文旨在求解的虚拟联盟制造企业协同制造问题是典型的离散优化问题，因此本文通过设计二维整数编码以及离散变异规则来改进基本的树种算法，并将该算法命名为离散树种算法(DTSA)。从之前的问题描述和问题分析中可以看出，个体编码一方面需要反映选择了哪些制造企业，另一方面需要体现哪些订单被分配到了哪些已经被选择的制造企业处。因此我们设计了二维整数编码来指定制造企业并分配订单。第一维编码由取值是0或1的M维向量，0表示该制造企业被纳入虚拟联盟之中，1表示该制造企业没有被纳入虚拟联盟之中。第二维编码是取值为1到M之间的整数的n维向量。假设有4个制造企业可供选择，公共订单服务平台接受了7个订单，我们利用图2举例说明该二维编码的组成。如图2所示，第一维编码说明第2个和第4个制造企业组成了虚拟联盟。在第二维编码中，订单1、2、4、6对应编码取值都不大于2，故这些订单都被分配到第2个制造企业处；订单3、5、7对应的编码取值都不小于2并且不大于4，故这些订单都被分配到第4个制造企业处。特别地，第二维编码对应的某些数值大于第一维编码指定的制造企业序号的最大值时，这些数值对应的订单都将被分配至序号最大的制造企业处。此外，根据引理3可知，第二维编码对应的订单应按照其基本加工时间从大到小顺序排列。

图2 二维离散编码示意图

4.3 适应度值测算方法

本文将最后获得的利润作为某一树木或者种子的适应度值。适应度值计算方法如下所示：

适应度值测算方法步骤1.针对某个个体,按照编码策略所述的虚拟联盟成员选择以及订单分配原则,确定虚拟联盟以及每个联盟制造企业所要加工的订单。步骤2.根据引理5所述的虚拟联盟成员替换规则,更新虚拟联盟成员的组成以及联盟企业所要加工的订单。步骤3.根据引理1所述的制造企业处订单完工时间的计算公式,计算每个联盟制造企业最后一个订单的完工时间。步骤4.根据引理4所述的总制造成本的计算规则,计算联盟企业的制造总成本。步骤5.根据目标函数,计算企业联盟的总利润,并将其作为此个体的适应度值。

从上述对树种算法框架和适应度测算方法的描述可知，离散树种算法的时间复杂度与传统的树种算法相比并未增加。离散树种算法的种群中共有N个个体，在每一次迭代中，每个个体需要进行一次适应度测算，该过程的时间复杂度不超过O(Mn2log(n))。因此，所提离散树种算法的时间复杂度不超过O(NMn2log(n))。

4.4 离散种子生成规则

为了使得树种算法能够处理本文提出的离散优化问题，本文设计了离散树种算法的种子生成规则用于子代种子的产生。考虑某一棵树木的某一个种子S={S1,S2}的产生过程，其中，S1={S11…S1M}，S2={S21…S2n}。假设该树木的位置表示为T={T1,T2}，当前最好解的位置为B={B1,B2}，本文给出如下的离散种子生成规则。其中，T1={T11…T1M}，T2={T21…T2n}，B1={B11…B1M}，B2={B21…B2n}。

离散种子生成规则第一维编码变异规则步骤1.令i=1步骤2.若rand

5 仿真实验

在本节，我们将所提的离散树种算法(DTSA)与已有的离散智能算法如，离散萤火虫算法(Marichelvam等)[13]、集合蛙跳算法(Eusuff等)[14]进行比较。简便起见，我们将离散萤火虫算法记为DFA，集合蛙跳算法记为SFLA。所有实验均在带有Intel Core i7-8550U CPU和16GB RAM的联想笔记本上运行。各个算法的性能由相对误差率来表示，具体计算公式如下：

其中，RPD表示算法的平均相对误差率，Zbest表示一次运行中三种算法求得的最好解，ZA表示某一算法求得的解。

5.1 仿真参数设计

本文的仿真实验主要涉及到算法本身参数和问题模型参数两个方面的参数，其中，算法参数有种群数目N、搜索趋势控制参数ST、算法迭代终止时间T；模型参数有订单数目n、订单oj的销售额sj、订单oj加工时间pj、可用的制造企业总数M、制造企业mi的单位时间制造成本fi、制造企业mi的启动成本gi、订单加工时的机器老化率a。算法参数N、ST、T直接影响到算法程序的运行时间和运行内存，我们利用田口法对这些参数进行调整。首先，我们为这3个参数设计了不同层次的参数水平，具体如表1所示。

在田口实验法确定参数水平的过程中，我们主要采用正交实验来替代全因子实验，这样可以大幅度地减少预实验的时间和成本。本文涉及的3因子和3水平正交实验表如表2所示，其中响应值为10次运行结果的平均值。

表1 算法不同参数水平设计

表2 3因子和3水平正交实验表

上述预实验涉及的问题模型的参数取值为：订单数目n为80，订单oj的销售额介于20到25之间，订单oj加工时间介于1和2之间，可用的制造企业总数M为3，制造企业mi的单位时间制造成本fi介于1和2之间，制造企业mi的启动成本gi介于100和200之间，订单加工时的机器老化率a介于0.05和0.10之间。根据表3的数据，我们给出了各个参数的效应图，如图3所示。从图3可以看出，N的最优参数水平为3，取值为40，ST的最优参数水平为2，取值为0.2，算法终止时间T的最优参数水平为1，取值为400。

图3 各个参数水平的主效应图

5.2 仿真实验结果及分析

在上述算法参数调整的基础上，考虑到模型参数对实验结果的影响，本文设计了包括小规模和大规模两类含有不同模型参数组合的算例。规模是相对于订单数目而言的，小规模算例中的订单数目不超过80，大规模算例中的订单的数目在100到200之间。两类参数的其余模型参数取值为：订单oj的销售额介于20到25之间，订单oj加工时间介于1和2之间，可用的制造企业总数M在大规模实验中介于3和5之间，在大规模实验中介于8和10之间，剩余参数取值和预实验相同。在上述算法参数和模型参数确定的基础上，我们分别对每个算例利用各个算法分别求解了100次，记录了每次试验的各个算法的RPD，为了直观的比较各个算法的结果，我们利用各个算法100实验的RPD数据绘制了折线图，如图4所示。

从图4可以看出，在大多数情况下，离散树种算法求解的结果要优于集合蛙跳算法和离散萤火虫算法。集合蛙跳算法和离散萤火虫算法之间并没有明显的优劣关系。为了进一步分析各个算法在统计学上的优劣性，我们分别计算了各个算法所有RPD的中位数、标准差和平均值。具体数据如表3所示。

图4a 订单60时实验结果

图4b 订单70时实验结果

图4c 订单80时实验结果

图4d 订单100时实验结果

图4e 订单150时实验结果

图4f 订单200时实验结果

表3 小规模和大规模算例实验结果

为了直观地比较各个算法中位数、标准差和平均值之间的关系，我们利用表3的数据制作了如下的折线图，如图5所示。

图5a 中位数对比图

图5b 标准差对比图

图5c 平均值对比图

从图5可以看出，离散树种算法求解结果的中位数、标准差、平均值均要比其他两种算法要低，这说明了所提算法在求解效果和求解的鲁棒性方面均要优于其他两种算法。

6 结语

本文考虑了虚拟制造联盟组建和虚拟联盟运行两阶段联合优化问题，在虚拟联盟组建阶段，主要涉及到企业联盟的成员选择问题；在虚拟联盟运行阶段，主要涉及到顾客订单分配和各个联盟企业的订单生产排序问题，特别地，我们考虑了联盟企业的机器老化效应。为了求解所提模型，我们提出了单一联盟企业处的最优化订单生产排序算法，并给出了多个联盟企业间的订单分配规则以及联盟企业成员选择规则。结合上述规则，开发了嵌入二维离散编码策略和离散种子生成规则的离散树种算法。最后一系列的仿真实验结果表明所提算法相较于离散萤火虫算法和集合蛙跳算法等离散智能优化算法而言，在求解质量和鲁棒性上具有一定的优越性。

在未来的研究中，我们将更加注重构建更为符合实际的问题模型，更多地考虑虚拟联盟企业存在的复杂的耦合关系。同时，开发更加有效的智能优化算法，提升已有解决方案的有效性和鲁棒性。