小波分析在GNSS-IR潮位反演中的应用

王 杰，何秀凤，王笑蕾，宋敏峰

小波分析在GNSS-IR潮位反演中的应用

王 杰，何秀凤，王笑蕾，宋敏峰

(河海大学 地球科学与工程学院，南京 211100)

针对全球卫星导航系统多径反射（GNSS-IR）反演潮位值时易出现时间分辨率不足，而当前常用的多模多频法不适用于所有测站，加窗法会使反演结果精度降低的问题，提出1种小波分析反演方法：利用小波变换分析方法提取信噪比序列的瞬时频率，然后反演瞬时潮位值；最后分别以美国SC02站17 d数据和香港HKQT站13 d数据加以验证，并与经典法、加窗法的反演结果进行分析比较。实验结果表明，用小波变换分析法反演潮位值的精度能达分米级，并且可由原先1段信噪比序列反演1个潮位值提升至单历元信噪比反演1个潮位值，反演点个数大幅增加。

多路径反射；信噪比；潮位监测；小波分析

0 引言

随着全球变暖，人们更加重视海洋气候变化所带来的问题。海面变化受气候变化影响，同时也影响着沿海城市人类的社会活动。近年来，全球卫星导航系统（global navigation satellite system, GNSS）与遥感相结合的技术正不断发展完善，这种新技术称为GNSS多径反射（GNSS interferometric reflectometry, GNSS-IR）。通过提取连续运行参考站（continuously operating reference stations, CORS）的信噪比（signal to noise ratio, SNR）数据进行频谱分析，进而反演出有效高度，具有部署简单、分布广泛等特点[1]。2009年文献[2]提出用于积雪厚度测量，接着推广到潮位测量中[3]，此后国内外基于GNSS-IR技术的潮位监测开始开展相关研究。国外方面：文献[4]提出在北极格林兰岛附近海域使用全球定位系统（global positioning system, GPS）反射信号成功反演了潮位高度变化；文献[5]利用GPS信噪比进行潮汐反射研究，精度达到10 cm；文献[6]利用多路径信号对5个GPS站进行潮位反演，潮位变化较大的区域反演精度为43 cm，潮位变化较小区域精度能达到6 cm左右。国内方面：文献[7]首次在我国进行了岸基GNSS海洋遥感实验；文献[8]首次采用北斗卫星导航系统（BeiDou navigation satellite system，BDS)在浙江大洋山海域进行海面测高实验，反演的海面高度精度达到了亚米级；文献[9]用SC02站的数据进行了不同时间跨度的潮位反演，与验潮站实测值相关系数均优于0.98；文献[10]利用站SC02数据反演该站附近海域14 a的潮位变化情况，反演精度为8 cm。经过学者大量研究验证，GNSS-IR可以有效监测潮位变化情况。

反演值的时间分辨率对获取潮位变化的信息有直接影响，在保证一定精度条件下，潮位反演值分辨率越高，对于潮波系数的探测、潮位分析和海平面的准确监测越有利。然而通常一段SNR序列只能反演得到1个时刻的潮位值，这样使得反演点数量有时不足并且不符合潮位时刻变化的特性。反演潮位常用的经典方法是L-S谱（Lomb-Scargle periodograms, LSP）分析法，接收机采样率越高，有效卫星弧段的SNR值就越多，反演效果也会越好。然而这种方法处理的数据具有时间跨度，更适合反演反射面较稳定的土壤湿度[11]、雪深[12]等，用来反演潮位便会有误差；同时由于反演值数量受空中有效卫星弧段的影响[13]，1个有效卫星弧段的SNR序列只能反演1个结果，有时反演值的数量不足，不利于潮位监测。针对反演值时间分辨率不足的问题，目前国内外解决办法主要归于以下2种：第1种是从GNSS多模多频方面着手，该方法能有效提高反演值时间分辨率，如国外使用了GPS和格洛纳斯卫星导航系统（global navigation satellite system, GLONASS）双系统的不同波段反演潮位[14-15]；国内用BDS 3个波段[16]和GPS、BDS、GLONASS 3个系统8个波段[17]反演潮位。但即使这样，有时反演点仍然很少，如文献[16]中26 d时间跨度反演点数量却不到200个。同时4系统的CORS站并不多，遇到单系统的CORS站这种方法也无法使用。第2种方法称为窗口L-S谱（windows LSP，WinLSP）分析法，即利用时间窗口或高度角窗口截取SNR序列，每个窗口得到1个反演值，由一变多。例如文献[18]用的窗口长度为800个SNR（约14 min）的窗口截取SNR序列，使得每天有近80个潮位反演值。文献[19]用窗口长度为5°的高度角窗口分别截取SC02和PBAY 2个站点的SNR序列，2者均能在十几分钟内得到50多个反演值。然而对于第2种方法，时间窗口选取有时太短，截取的SNR序列不能满足频谱分析的要求，或是用高度角窗口截取后反演点增多，但反演精度会降低，而且有些测站反演潮位的有效高度角区间较小，这种方法便无法使用。

本文针对反演值时间分辨率不足的问题，利用小波分析方法提取SNR序列的瞬时频率反演潮位值，分别以美国SC02站17d数据和香港HKQT站13 d数据加以验证，并与LSP、WinLSP 2种方法反演结果进行分析比较。

1 GNSS-IR反演原理及小波时频分析

1.1 GNSS-IR反演潮位原理

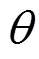
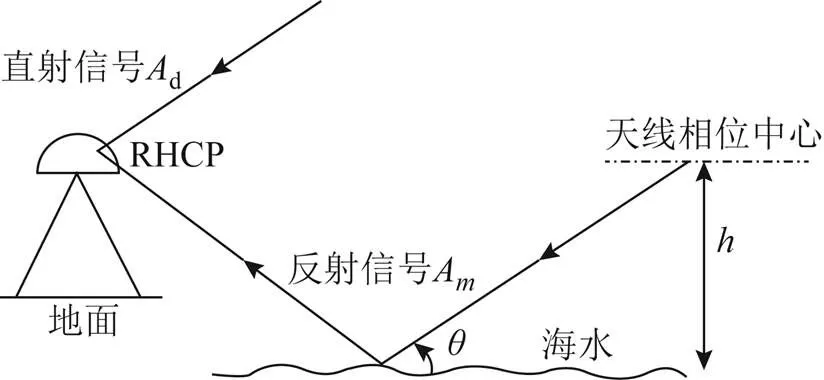
图1 GNSS-IR反演潮位原理

图2为卫星的SNR时序图，在低高度角情况下SNR振荡明显，随后趋于稳定。通过对低高度角的SNR序列频谱分析便可得到反射面参数。由于直射信号振幅远大于反射信号振幅，为减少后续频谱分析产生虚假高峰，2次多项式拟合作为趋势项的直射信号，去趋势后得到的SNR残差序列[20]表示为

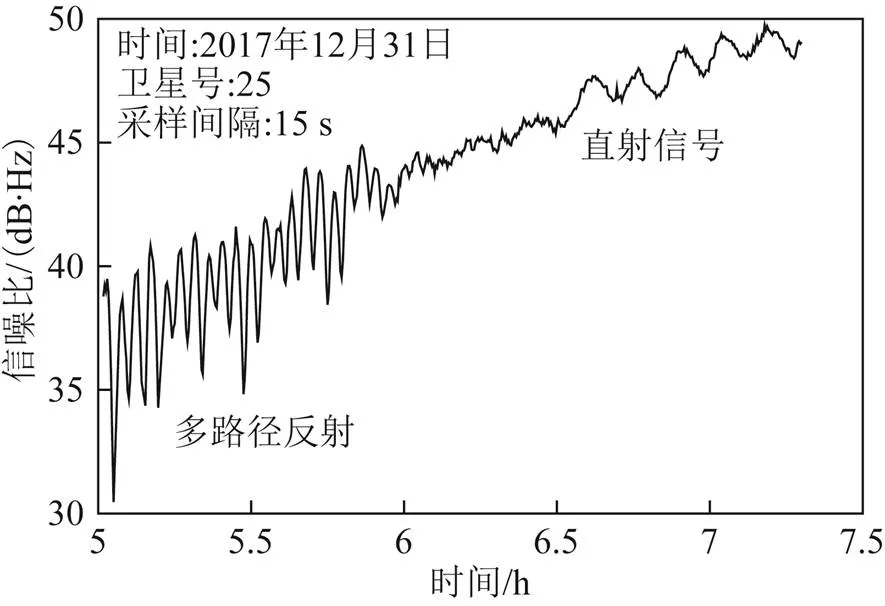
图2 信噪比时序

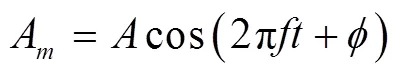
对式（2）进行LSP分析即可得到有效高度值，结果如图3所示。

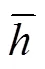
1.2 小波分析提取瞬时潮位

1.2.1 小波分析

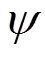
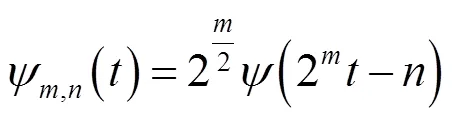
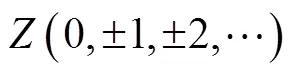
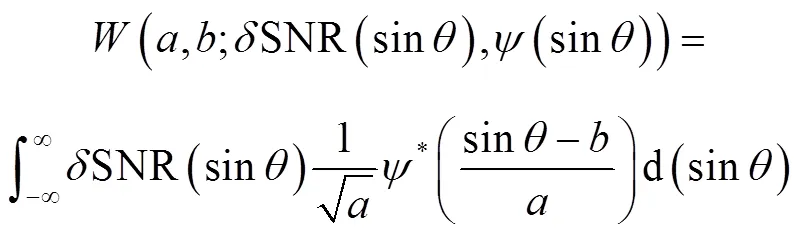
1.2.2 小波分析提取潮位反演值

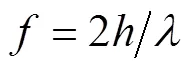
图4 SNR残差序列与小波时频分析

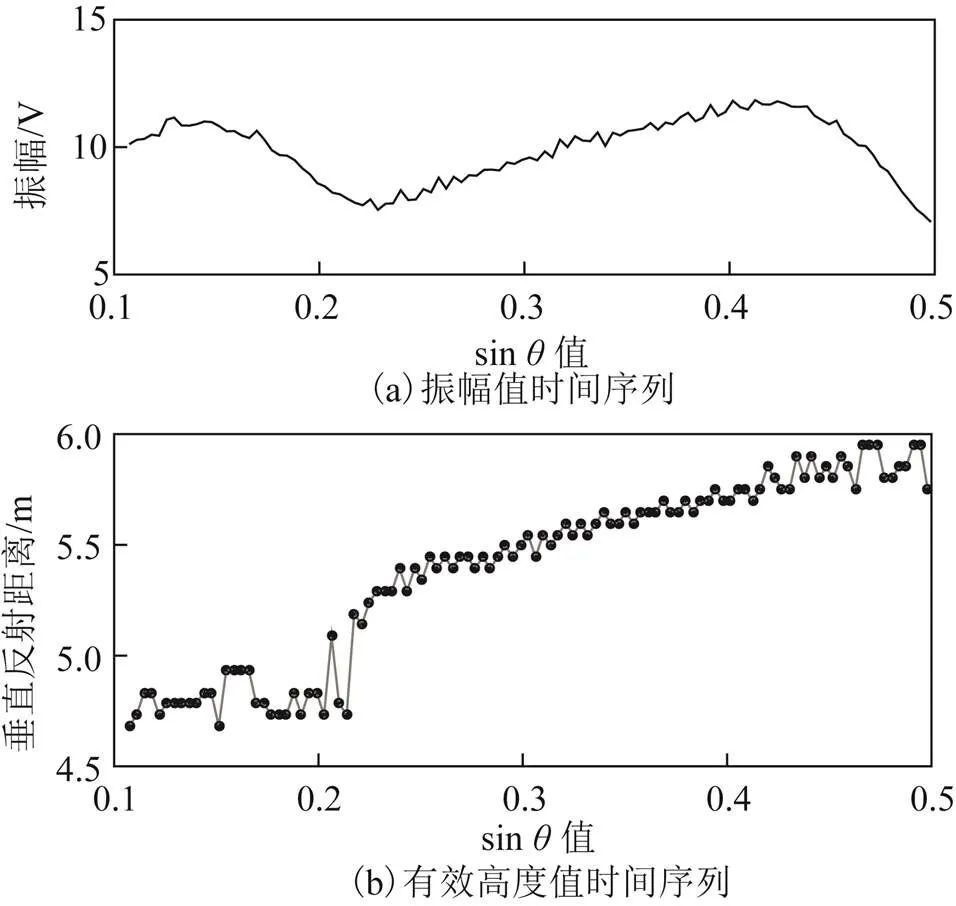
图5 最大振幅值及对应有效高度

图5（a）中，振幅的2个峰值位于0.15和0.43附近，与图4（b）的2个能量聚集处分别对应。根据以上步骤即可提取SNR序列的瞬时频率，进一步得到反演潮位值。对于该方法反演的粗差，这里利用LSP反演结果拟合潮波曲线进行剔除。

2 实验与结果

2.1 香港HKQT站算例

HKQT站属于香港卫星定位参考站网，装备TRIMBLE NETR5型接收机，位于HKQT站（如图6所示）附近的Quarry Bay验潮站可以提供实测数据。算例用2016年年积日第45~57天共13 d GPS L1波段数据进行验证。由于站点环境原因，高于9°的卫星反射信号会被遮挡，故选取有效高度角区间4~9°，有效海面相对于接收机的方位角区间-60~105°。

图6 HKQT站点及其周边环境

分别用LSP、WinLSP和小波变换反演13 d的潮位值，其中WinLSP用长度为4°，步长为1°的高度角窗口截取，即[4° 8°]、[5° 9°]。反演结果分别与验潮站实测值进行对比，残差时间序列和反演结果如图7、图8所示。

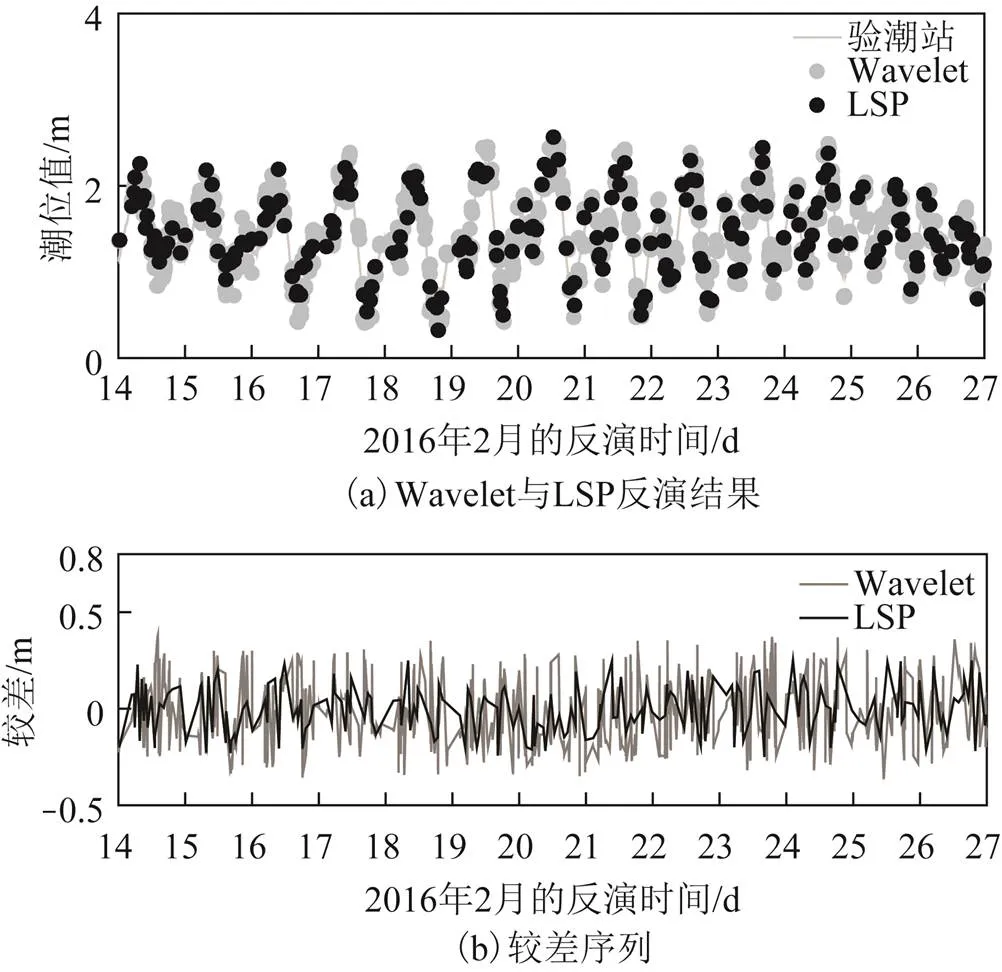
图7 Wavelet与LSP对比结果

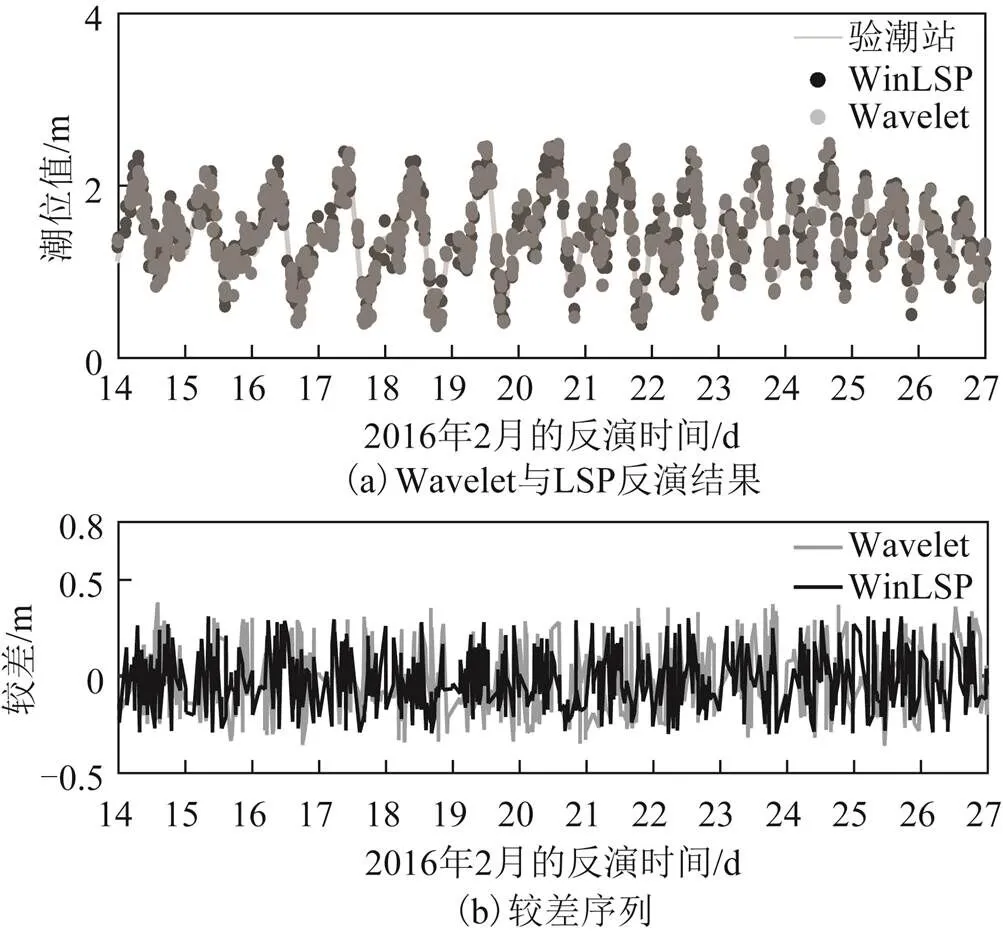
图8 Wavelet与WinLSP对比结果

图7（a）中：灰色曲线为验潮站实测值；黑色圆点为LSP反演结果，精度为12.39 cm；浅灰色圆点为Wavelet法反演结果，精度为16.08 cm。图8（a）中，深灰色圆点为WinLSP反演结果，精度为14.67 cm。图7（b）、图8（b）为3者与验潮站值较差序列图，可以看出3者与实测值的较差均在0处上下波动，LSP的波动范围最小，精度更高。Wavelet与WinLSP波动幅度相当，2者精度均低于LSP。WinLSP方法对高度角加窗后每个窗口中高度角的区间变小，即将1个长的SNR残差序列分割为几个短的SNR残差序列，因此在进行频谱分析后其结果质量会降低。而Wavelet方法极其依赖于SNR的质量，受噪声影响大，反演结果质量也会降低。3者与实测值对比结果如表1所示。

表1 HKQT站3种方法反演结果

从表1可以看出：LSP的反演精度最高；WinLSP的反演精度高于Wavelet，而Wavelet的反演点数量最多，反演值时间分辨率有大幅提高。

图9为2月26日当天3种方法反演值数量对比细节图，当日1时、4时及23时内，天空中因GPS卫星无有效弧段可用，3种方法没有反演结果。在2时、21时内有卫星弧段可用，但反演值为粗差均被剔除，3种方法同样没有有效值。而在6时、11时、12时、15时和17时内，LSP和Wavelet无有效值可用，WinLSP有可用反演值，得益于当SNR质量较差时，WinLSP能在一定程度上将SNR数据中质量差的部分与质量好的部分进行分割，反演值符合要求的被保留，误差大的被剔除。但因加窗分割使其高度角区间变小，故反演精度也会降低。在剩余时间内，由图可知用Wavelet法反演结果数量较LSP法和WinLSP法明显增多，3种方法反演的当天潮位值在数量变化趋势上近似，这是因为3者都是基于同1个SNR弧段进行分析，并且Wavelet法依赖于SNR质量，所以SNR质量高，LSP反演结果有效，Wavelet同样有有效反演值；SNR质量低，LSP结果误差较大而被剔除，则Wavelet也无有效结果可用，2者呈对应关系。

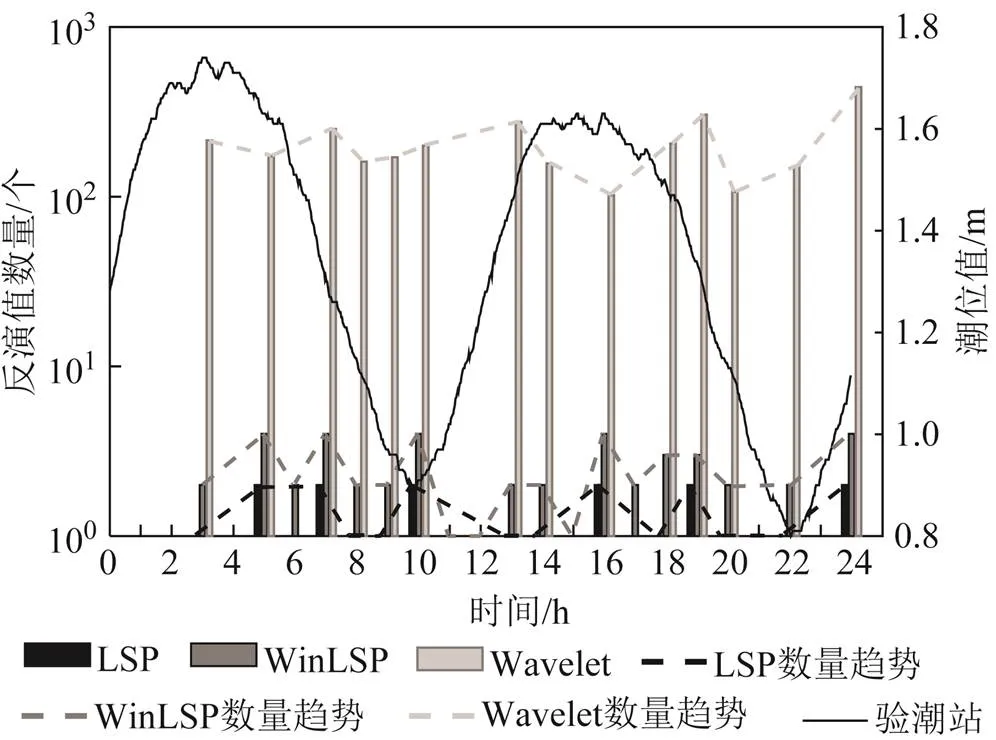
图9 第13天反演结果数据量对比细节

2.2 美国SC02站算例

SC02站位于美国华盛顿州，站点安装Trimble NETRS接收机，并配备Trimble TRM29659.00天线，距离该站300m远有1个潮汐测量仪，可提供实测潮位数据（如图10所示）。

图10 SC02站点及其周边环境

算例用2017年年积日第128~144天共17 d GPS L1波段数据进行验证，高度角选取5~15°，方位角选取50~240°。3种方法反演结果如图11所示，其中WinLSP反演用长度为5°、步长为2.5°的高度角窗口截取SNR序列，即[5° 10°]、[7.5° 12.5°]、[10° 15°]。

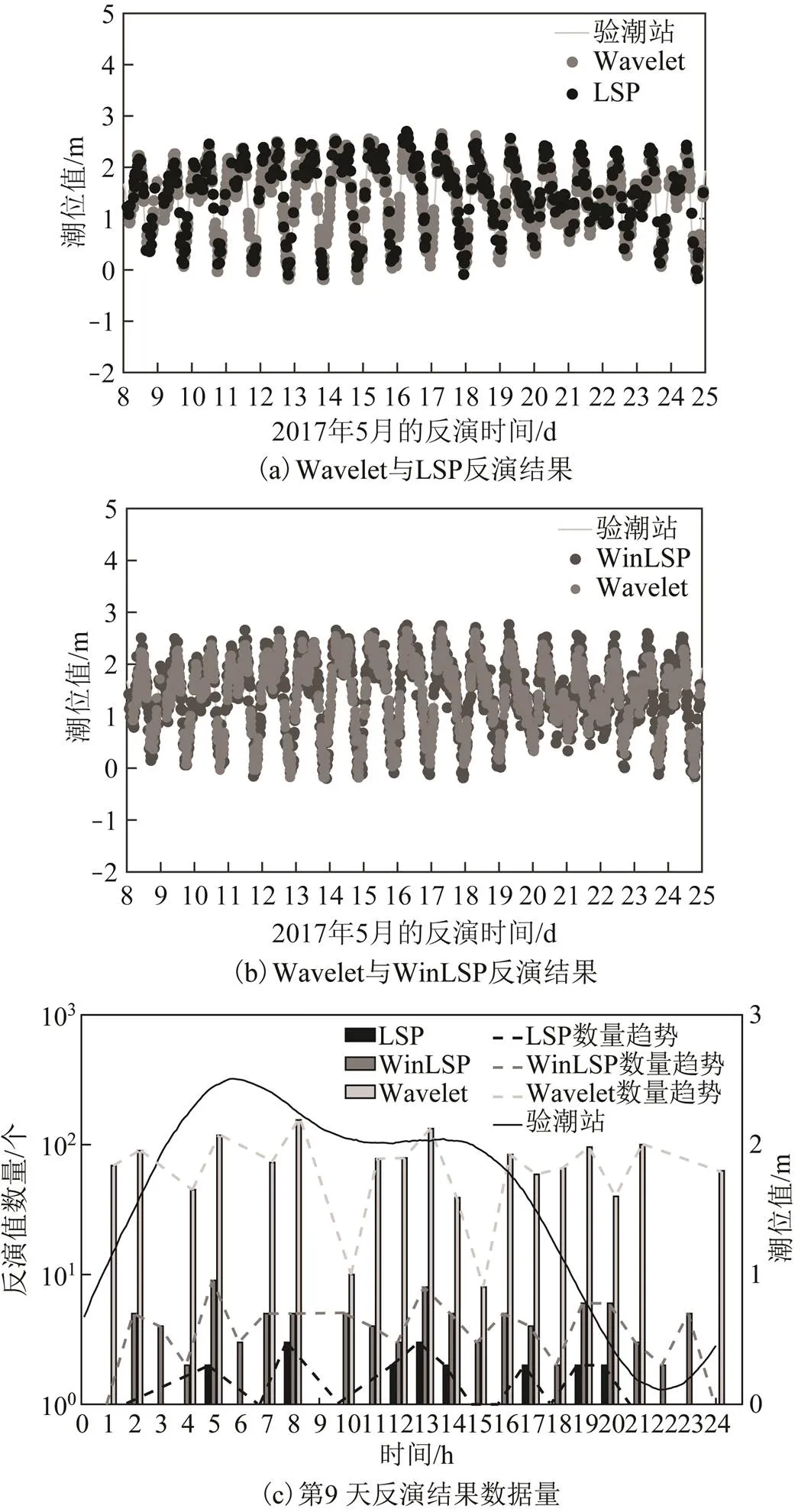
图11 SC02站反演结果

图11（a）中：灰色曲线表示验潮站实测值；浅灰色圆点表示Wavelet反演结果，反演精度为14.47 cm；黑色圆点表示LSP反演结果，反演精度为13.09 cm。对比LSP反演结果可以看出Wavelet方法反演结果的时间分辨率明显提高。图11（b）中深灰色圆点表示WinLSP反演结果，反演精度为22.85 cm。图11（c）为5月16日3种方法的反演值数量对比细节图，可以看出3种方法反演结果数量变化趋势有良好的一致性。其中，在当日第1、3、4、6、9、11时内LSP反演值为粗差而被剔除，第22、23、24 h内，由于潮位较低，卫星经海面的反射信号强度减弱，LSP无有效反演结果。WinLSP与Wavelet结果分布情况较LSP表现更好，且在第1、4、11、24 h内，LSP无结果但Wavelet仍有反演值，这期间Wavelet反演结果与验潮站实测值的标准差为9.69 cm。3种方法与验潮站实测值总体对比情况见表2，误差分析及相关系数见图12和图13。

表2 SC02站3种方法反演结果

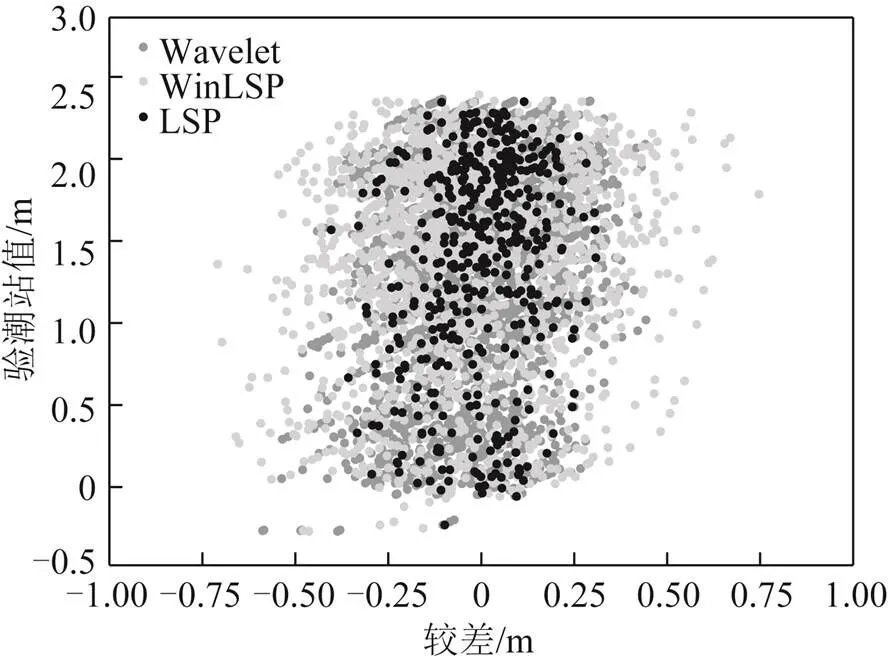
图12 较差分布

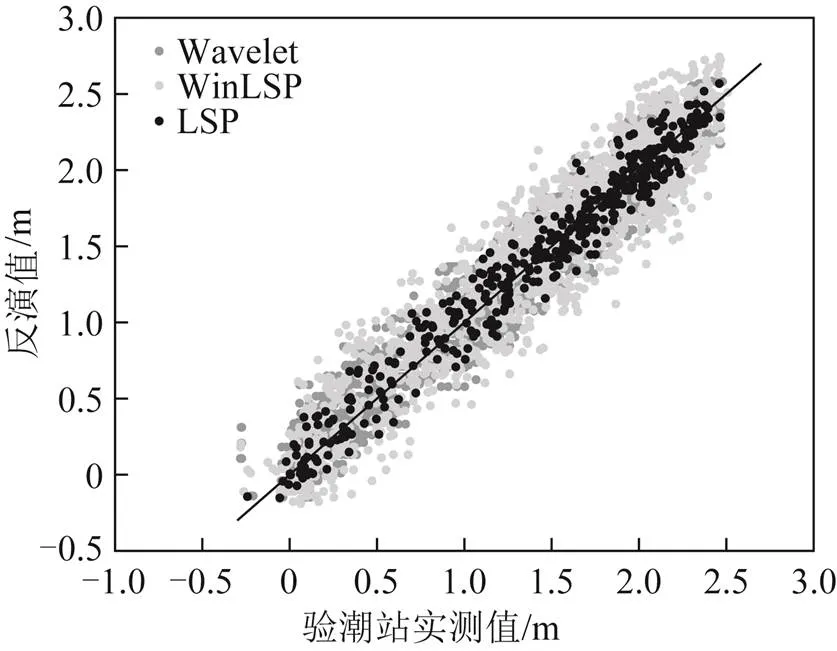
图13 反演值与验潮站相关系数分析

结合图12与图13分析，用 LSP、WinLSP和Wavelet 3种方法反演的结果与实测值较差均以0为中心左右分布，说明其反演结果不存在系统误差。3种方法反演值与验潮站实测值的相关系数均优于0.96，其中LSP方法反演结果的精度最好，Wavelet方法略低，WinLSP法最差。同时，图中在潮位较高区域，3种方法的误差分布明显较为集中，这是由于随着潮位升高，海水反射面与测站的垂直距离逐渐减小，测站接收到经海面反射的卫星信号增强，反演结果相比低潮位情况更理想，因此得到的有效反演值会更多。

LSP和Wavelet都是基于整段SNR序列反演潮位值，而WinLSP则是用高度角窗口将SNR序列由1段截取为3段再分别用LSP进行反演；这样虽然有利于潮位实时监测，但结果精度却降低。若对分段的SNR序列分别用小波分析处理，则其结果如图14所示。

图14 整体与分段Wavelet较差序列

图14中深灰色圆点表示每个SNR整体弧段的Wavelet反演结果与实测值较差序列，浅灰色圆点表示SNR加窗分段以后的Wavelet反演结果与实测值较差序列。分段后的Wavelet反演结果精度为20.34 cm，精度较整体分析的结果下降了40.57 %，与验潮站的相关系数由0.96下降为0.87。

经以上案例分析，验证了Wavelet方法可用于GNSS-IR潮位反演并且提高反演值时间分辨率，能够获得更多潮位变化的信息量。同时基于整段SNR序列分析的Wavelet反演精度更好，而对于分段的SNR短序列，其反演结果精度相比较差，虽然在实时性上得到了一定的提高，但精度下降严重。这是因为随着弧段数据的减少，频谱分析时的准确度会降低，如果逐渐减少弧段的长度以提高潮位监测的实时性，精度无法达到要求，不利于潮位的实时监测。

3 结束语

本文针对GNSS-IR反演潮位时间分辨率不足的问题，从处理SNR时间序列方面着手，利用小波变换分析提取单历元SNR的瞬时频率进而反演出潮位的变化情况。同时，分别用LSP、WinLSP 2种方法反演潮位结果作为对比。与验潮站实测值相比，对于HKQT站：LSP反演结果标准差为12.39 cm，有214个反演点；WinLSP反演结果标准差为14.67 cm，有553个反演点，Wavelet反演结果标准差为16.08 cm，反演点个数为38 570；3者与实测值相关系数均优于0.95。对于SC02站：LSP反演结果标准差为13.09 cm，精度最高，有432个反演点；Wavelet反演结果标准差为14.47 cm，精度稍低，反演点个数达29703个；WinLSP反演结果标准差为22.85 cm，有1770个反演点，精度最低；3者与实测值相关系数均优于0.96。

对于潮位动态改正，常需要利用反演值拟合潮波函数求解反射面高度变化率，改正效果依赖于潮波函数的拟合程度；而用小波变换反演1段SNR序列得到连续潮位值，可直接进行反射面高度变化率的求解。并且用小波变换分析法能大幅提高反演值时间分辨率，有利于获取更多的潮位变化情况。然而该方法极易受噪声影响，对质量不好的SNR分析结果会存在大量粗差，有待进一步对信号降噪处理。同时这种方法不能离开LSP法单独使用，因为其粗差的剔除需要根据LSP结果的整体拟合来处理。因此遇到反演值时间分辨率不足的问题时，小波变换分析可以作为LSP反演潮位值的补充，进而有利于更好地发挥GNSS-IR技术在潮位变化监测中的重要作用。

[1]李惟, 朱云龙, 王峰, 等. GNSS多径信号模型及测高方法[J]. 北京航空航天大学学报, 2018, 44(6): 126-132.

[2]LARSON K M, GUTMANN E D, ZA VOROTNY V U, et al. Can we measure snow depth with GPS receivers?[J]. Geophysical Research Letters, 2009, 36(17): L17502.

[3]ROUSSEL N, RAMILIEN G, FRAPPART F, et al. Sea level monitoring and sea state estimate using a single geodetic receiver[J]. Remote Sensing of Environment, 2015(171): 261-277.

[4]SEMMLING A M, BEYERLE G, STOSIUS R , et al. Detection of Arctic Ocean tides using interferometric GNSS-R signals[J]. Geophysical Research Letters , 2011, 38(4) : 155-170.

[5]LARSON K M , LÖFGREN J S, HAAS R. Coastal sea level measurements using a single geodetic GPS receiver[J]. Advances in Space Research, 2013, 51(8): 1301-1310.

[6]LOFGREN J S, HAAS R, SCHERNECK H G. Sea level time series and ocean tide analysis from multipath signals at five GPS sites in different parts of the world[J]. Journal of Geodynamics, 2014(80): 66-80.

[7]王鑫, 孙强, 张训械, 等. 中国首次岸基GNSS-R海洋遥感实验[J]. 科学通报, 2008, 53(5): 589-592.

[8]ZHANG Y, TIAN L, MENG W, et al. Feasibility of code-level altimetry using coastal BeiDou reflection (BeiDou-R) setups[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(8): 4130-4140.

[9]张双成, 南阳, 李振宇, 等. GNSS-MR技术用于潮位变化监测分析[J]. 测绘学报, 2016, 45(9): 1042-1049.

[10]匡翠林, 刘凯, 周要宗. 基于GPS信噪比数据观测海平面变化研究[J]. 海洋测绘, 2018, 38(6): 40-43.

[11]LARSON K M, SMALL E E, GUTMANN E, et al. Using GPS multipath to measure soil moisture fluctuations: initial results[J]. GPS Solutions, 2008, 12(3) : 173-177.

[12]LARSON K M, SMALL E E. Estimation of snow depth using L1 GPS signal-to noise ratio data[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016, 9(10): 4802-4808.

[13]LARSON K M , RAY R D , WILLIAMS S D P . A 10-year comparison of water levels measured with a geodetic GPS receiver versus a conventional tide gauge[J]. Journal of Atmospheric and Oceanic Technology, 2017, 34(2): 295-307.

[14]LÖFGREN J S, HAAS R. Sea level measurements using multi-frequency GPS and GLONASS observations[J]. EURASIP Journal on Advances in Signal Processing, 2014, 2014(1): 50.

[15]STRANDBERG J , HOBIGER T , HAAS R. Improving GNSS-R sea level determination through inverse modeling of SNR data[J]. Radio Science, 2016, 51(8): 1286-1296.

[16]李彬彬. 北斗反射信号海面测高技术的研究[D]. 上海: 上海海洋大学, 2017.

[17]陈发德, 刘立龙, 黄良珂, 等. 基于多模GNSS-MR海平面测高研究[J]. 地球物理学进展, 2018, 33(5): 1767-1772.

[18]LARSON K M, RAY R D, NIEVINSKI F G, et al. The accidental tide gauge: a GPS reflection case study from Kachemak Bay, Alaska[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1200-1204.

[19]WANG X L, ZHANG Q, ZHANG S C. Water levels measured with SNR using wavelet decomposition and Lomb-Scargle periodogram[J]. GPS Solutions, 2018, 22(1): 22-28.

[20]LARSON K M, SMALL E E, GUTMANN E D, et al. Use of GPS receivers as a soil moisture network for water cycle studies[J]. Geophysical Research Letters, 2008, 35(24) : L24405.

[21]马秀红, 曹继平, 董晟飞. 小波分析及其应用[J]. 计算机技术与发展, 2003, 13(8): 93-94.

[22]TORRENCE C, COMPO G P. A practical guide to wavelet analysis[J]. Bull Am Meteorol Soc, 1998, 79(1): 61-78.

Application of wavelet analysis in tidal by GNSS-IR

WANG Jie,HE Xiufeng,WANG Xiaolei,SONG Minfeng

（School of Earth Sciences and Engineering, Hohai University, Nanjing 211100, China)

Aiming at the problems that it is apt to be insufficient for the time resolution, and two usual methods, the multi-system method is not applicable to all stations, and the windowing method reduces the accuracy of the inversion results in the tide value inversion of GNSS-IR, the paper proposed an inversion method using wavelet analysis: the instantaneous frequency of signal-to-noise ratio (SNR) sequence was extracted with the wavelet transform analysis method, and the instantaneous tide level values were inverted; then the 17-day data of the US SC02 station and the 13-day data of the Hong Kong HKQT station were used to implement the verification, and the inversion results of the classical method and windowing method were used to do the comparative analysis finally. Experimental result showed that: the method could have an accuracy of dm level, and a tide value could be inverted with a single epoch SNR, improved from inverted with a sequence of SNR, which means an increased number of inverted points.

multipath reflectometry; signal-to-noise ratio (SNR); tidal level monitoring; wavelet analysis

P228.4

A

2095-4999(2020)02-0082-08

王杰，何秀凤，王笑蕾，等. 小波分析在GNSS-IR潮位反演中的应用[J]. 导航定位学报, 2020, 8(2): 82-89.（WANG Jie，HE Xiufeng, WANG Xiaolei, et al. Application of wavelet analysis in tidal by GNSS-IR[J]. Journal of Navigation and Positioning, 2020, 8(2): 82-89.）

10.16547/j.cnki.10-1096.20200214.

2019-08-15

国家自然基金项目（41830110）。

王杰（1996—），男，安徽天长人，硕士研究生，研究方向为GNSS空间环境分析。

何秀凤（1962—），女，江苏泰州人，博士，教授，研究方向为卫星导航定位。