多潮位站海道地形测量潮位控制方法研究

，，，

(1.长江水利委员会水文局 长江三峡水文水资源勘测局，湖北 宜昌 443000；2.长江宜昌航道局，湖北 宜昌 443000)

随着沿海及近海地区的开发与利用，海洋航运、港口码头修建、渔业养殖等人类活动愈加频繁，对海洋的分析研究要求也越来越高，这势必会对获取的海洋信息的详细程度要求越来越高[1]。大面积海洋测绘精度已经逐步实现了由小比例尺测绘资料向中小比例尺资料的过渡。因此，传统的通过用沿岸设立潮位站[1]，对大面积海域的测量资料进行单站潮位改正的测绘方式已经无法满足精度的要求，需将目光投向对测量资料进行多站潮位改正这一研究方向。然而受海洋潮汐、地球曲率、涌浪等诸多外界因素的影响，多潮位站海道地形测量对潮位站的布设、基面关系的确定以及潮位改正方法的要求较为严格。虽然针对每种技术要求都有多种处理方法，但多潮位站海道地形测量的综合性较强，难度较大，从而导致该类项目实施困难。

本文主要对多潮位站海道地形测量潮位控制、基面计算与传递、潮位改正方法等方面进行分析研究，提出切实可行的技术路线，以便于进一步指导实际工作中多潮位站海道地形测量潮位控制方法问题。

1 测量关键技术原理分析

多潮位站海道地形测量关键技术有两个。

(1)潮位控制问题。包括临时潮位站布设、临时潮位站数据联测和潮位改正方法。沿岸临时潮位站的布设较为简单，且潮位站零点可通过水准测量等方法联测求得。而海上临时潮位站的布设较为困难，既要求水位计固定不动、安全稳定，又要求零点高程准确可求，这对技术和设备的要求较高。

(2)基面计算与传递。与陆地测量或内河地形测量不同，海洋测量有其独特的基准起算面，即深度基准面。我国多用理论最低潮面来定义深度基准面。如何解决不同测区理论最低潮面的计算与传递就成为一大关键问题。

下面针对这两大关键问题所要求的技术原理进行分析和阐述。

(1)最小二乘拟合模型。对于海上临时潮位站的零点推算最为精确可靠的方法，是根据沿岸基准潮位站与海上潮位站潮位曲线的相关性分析，采用最小二乘拟合模型推算[2]。

如图1所示，以时间为X轴，潮位值为Y轴，曲线TA(t)与TB(t)为两个临时验潮站同步潮位曲线，两条同步潮位曲线存在3个参数的差异：水平位移即两潮位间的潮时差δAB；垂直位移即两验潮站的基准面偏差εAB(应用到本文为两验潮站的水尺零点差)；同步潮位值的比值即潮差比γAB。曲线TA(t)与TB(t)存在以下关系：

TB(t)=γABTA(t+δAB)+εAB

(1)

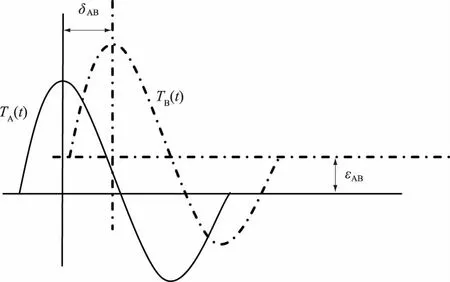
图1 最小二乘拟合法模型

(2)半潮差法。当临时潮位站附近有一个长期或短期潮位站时，临时潮位站的理论最低潮面可通过长期或短期潮位站的基面关系推算求得。根据《水运测量规范》(JTS131-2012)[3]所述，在大潮期同步观测两站潮位2～3 d，计算同步期平均海面。两站潮差差值不大于 0.1 m时，临时潮位站的深度基准面与同步期平均海面的高差，可借用邻近长期或短期潮位站的深度基准面与同步期平均海面的高差值；当两站潮差差值大于0.1 m时，临时潮位站深度基准面与同步期平均海面的高差应按下式计算：

(2)

式中，L′x为临时潮位站深度基准面与同步期平均海面的高差，m；L为长期潮位站深度基准面与同步期平均海面的高差，m；Px为临时潮位站同步期的平均半潮差，m；P为长期潮位站同步期的平均半潮差，m。

(3)潮汐调和分析。当临时潮位站附近无长期潮位站或长期潮位站离测区较远，可根据潮汐调和分析求解临时潮位站的基面转换关系。

由潮汐理论[4]知，海洋中的潮汐主要是由月球和太阳对地球的引潮力所致。所谓调和分析，就是把由月球等天体引起的复杂的潮汐现象，分离成由许多假想天体相对于地球作均速圆周运动而产生的潮汐(即分潮)之和。即对某一潮位站，在任意t时刻的潮高h(t)可表示为

h(t)=H0+

(3)

其中，H0为平均海平面；fk为节点因子；Rk为分潮角速度；(v0+u)k为分潮初相；Hk,gk为分潮调和常数。

利用M2、S2、N2、K2、K1、O1、P1、Q1、M4、MS4、M6、Sa、Ssa等13个分潮的调和常数，根据弗拉基米尔法可计算出理论最低潮面与高程基准的基面偏差。

(4)二步内插法潮位改正[5]。设A1、A2、A3三个潮位站某时刻的潮位分别为Z1、Z2、Z3，求P点的潮位，如图2。

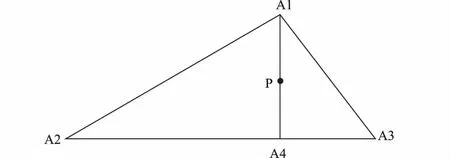
图2 二步内插法示意

由A1、A2、A3和P的坐标，可联解求得A2A3与A1P两个直线方程，得出A4的坐标，然后在直线A2A3上以这两点潮位按距离内插得到A4的潮位;再在直线A1A4上，以A1A4的潮位线性内插求得测点P的潮位:

ZP=(Z4-Z1)/SA1A4×SA1P+Z1

(4)

Z4=(Z2-Z3)/SA2A3×SA4A3+Z3

(5)

式中，SA1A4、SA1P、SA2A3和SA4A3分别为A4与A1、A1与P、A2与A3和A4与A3的距离。

2 多潮位站海道地形测量潮位控制应用

(1)潮位站布设。以江苏盐城射阳港水下地形测量项目为例，为满足规范规定潮位控制要求，在沿岸布设1，2，3号3个临时潮位站，其中射阳河口码头站2号为基准验潮站，连续观测1个月，用于潮位调和分析。测区远岸端临时潮位站4号抛投水位自记仪。潮位站分布图如图3所示。

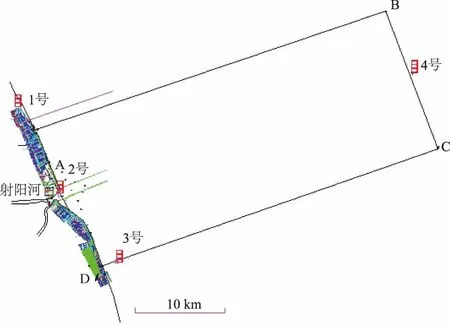
图3 临时潮位站位置

(2)临时潮位站零点联测。对于1，2，3号岸边潮位站的零点可通过水准联测和人工比测数据计算潮位站水尺零点。位于海上的4号潮位站，无法通过水准联测的方式确定水尺零点，采用最小二乘拟合传递推估技术(曲线拟合法)传递临时潮位站的水尺零点。

(3)基面计算与传递。该次实验数据中各潮位站的1985国家高程基准与理论最低潮面之间的基面关系采用两种方法相互验证，确保基面关系的准确性。

方法一是在射阳河口“2号”收集30 d的潮位观测资料，采用潮汐调和分析法计算出M2、S2、N2、K2、K1、O1、P1、Q1、M4、MS4、M6等11个分潮的调和常数；Sa、Ssa分潮的调和常数，由长期验潮站连云港站(射阳港北120km)1 a以上的潮位观测资料求得，最后采用弗拉基米尔法计算出理论最低潮面与1985国家高程基准的基面偏差。

方法二是收集附近长期验潮站大丰站(射阳港南约60 km)与射阳河口2号一个月的同步潮位数据，以及大丰站1985国家高程基准与理论最低潮面的关系，根据交通运输部《水运测量规范》(JTSB1-2012)[3]7.4.4.3中所述方法，将基面关系传递到测区。

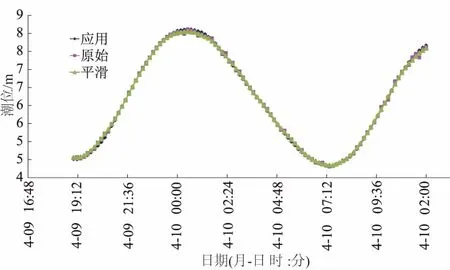
图4 潮位数据预处理示意

3 实验数据处理与分析

(1)潮位数据预处理。由于海洋环境恶劣，受涌浪、行船等因素的影响，水位自记仪原始记录数据多为锯齿状，为了得到真实平滑的潮位资料，需要对原始潮位资料做平滑预处理。方法有小波滤波处理[6]、MATLAB平滑拟合函数、人工干预等，本次采用MATLAB平滑拟合函数方法。

如图4所示，洋红色锯齿状曲线表示原始水位数据，灰色表示经过平滑拟合后的数据，蓝色表示实际应用潮位数据。由图可以看出，涨落潮时使用平滑拟合函数与实际潮位数据吻合较好，高低平潮时拟合数据与实际值有一定出入，需要人工干预处理。

(2)潮位站零点联测。沿岸临时潮位站可通过水准联测方式测出潮位站基点高程，再通过每天高低潮时人工验潮比测推算潮位站零点高程；海上临时潮位站通过最小二乘拟合模型传递。1985国家高程基准的水尺零点最小二乘拟合成果见表1。

表1 射阳河口“4号”最小二乘拟合成果

注：水尺零点采用-17.43 m。

(3)基面计算与传递。方法一是采用潮汐调和分析法求解，即在测区基准验潮站，射阳河口“2号”对该站30 d的潮位观测资料，采用潮汐短期调和分析法计算出M2、S2、N2、K2、K1、O1、P1、Q1、M4、MS4、M6等11个分潮的调和常数，见表2。

表2 短期调和分析成果

收集附近长期站1 a以上的潮位观测资料，采用潮汐长期调和分析法求解Sa、Ssa分潮的调和常数，由于该项目没有收集到长期站1 a的潮位观测资料，现用连云港2007年全年潮位资料做数据分析，调和分析成果见表3。

表3 长期调和分析成果

最后采用弗拉基米尔法计算出理论最低潮面在平均海平面下的高度L为1.93 m。平均海平面的计算采用面积包围法，求解同步期平均海平面的高程M为0.19 m。理论最低潮面的1985国家高程基准高程H=L-M=1.74 m。

方法二是根据长期潮位站大丰站理论最低潮面与1985国家高程基准的基面关系，采用半潮差法将基面关系传递到测区临时水位站。大丰站基面关系见图5。平均半潮差P=1.81 m，1985国家高程基准平均海平面D=0.21 m。“2号”潮位站基面关系见图6。平均半潮差PX=1.13 m，1985平均海平面DX=0.18 m。

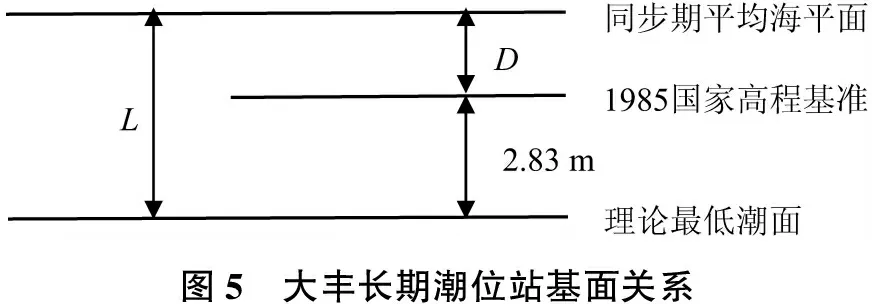
图5 大丰长期潮位站基面关系

图6 “2号”潮位站基面关系

由上面分析可以看出，通过两种方法推算基准站“2号”站的基面转换关系符合性较好。

(4)潮位改正。对测区数据进行分区处理，采用HYPACK三站潮位改正模块内插出各个水深点的潮位，进行逐点潮位改正。

4 结 语

本文对多潮位站海道地形测量潮位控制方法进行研究，着重对潮位控制和基准面计算与传递进行分析。针对潮位站零点传递问题，引入潮位改正中的最小二乘拟合原理，有效地解决了海上临时潮位站基面传递问题。针对测区理论最低潮面的计算问题，采用半潮差法与潮汐调和分析法相互验证，确保求解的基面关系准确可靠。