经验模态分解法在PPK潮位测量中的应用

胡小雷，刘小喜

（中交上海航道勘察设计研究院有限公司，上海 200120）

0 引言

在港口与航道工程中，潮位资料是重要的参考资料[1]。为获取临时潮位资料，目前常用的方法有潮位推算、抛设压力验潮仪、GNSS验潮等。潮位推算法受限于精度问题，不能直接用于生产[2]。抛设压力验潮仪面临仪器丢失导致数据空白、零点漂移、验潮仪在水下滑动致使数据失真等问题[3-4]。GNSS验潮可分为RTK验潮、PPK验潮和PPP验潮等，其原理均是从GNSS观测的瞬间水面高程中获取潮位数据，其精度主要受GNSS高程精度控制，而GNSS高程随时间呈非平稳性、明显的周期性变化特征。为去除GNSS高程中的长期趋势项及各类噪声，需要对GNSS高程进行滤波处理。目前，常用的滤波方法有傅里叶变换、小波变换，但傅里叶变换仅适用于平稳信号，小波变换则需要预先设定小波基函数，缺乏自适应性，二者均不适合处理具有非平稳、非线性的GNSS高程数据[5]。经验模态分解（EMD）完全抛开了基函数的束缚，仅仅依据数据自身的时间尺度特征来进行信号分解，具备自适应性[6]。鉴于此，本文利用经验模态分解法对PPK潮位数据进行分解，将去除噪声后的潮位资料进行数据重构，并与同期长期潮位站数据进行比对分析，以探讨该方法在PPK潮位测量中的适用性。

1 数据来源

2018年4月16—19日分别在连云港车牛山站、油码头站、开山岛站等3个长期验潮站附近水域开展PPK潮位测量，基准站架设于东西连岛（L090），各验潮站PPK潮位测量时间段见表1，各验潮站位置及基准站位置见图1。PPK潮位观测系统由Trimble SPS 855双频接收机、TSS姿态测量系统组成，在测量船重心上方位置分别固定GNSS接收机和TSS传感器，测定GNSS天线在船体坐标系下到水面的垂直距离。GNSS的采样频率为1 Hz，卫星截止高度角为10°，TSS传感器的采样频率为5 Hz。PPK潮位测量期间，同步收集车牛山站、油码头站、开山岛站长期潮位站潮位资料。PPK潮位测量期间天气状况良好。

表1 各验潮站PPK潮位测量时段Table 1 Tidal level measurement period of PPK at each tide gauge station

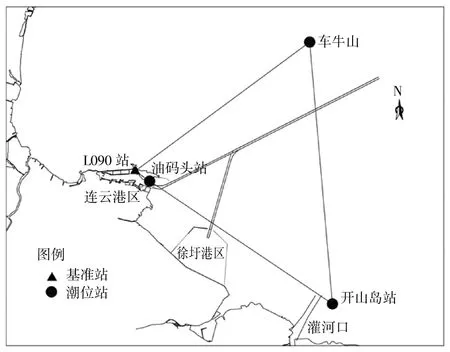
图1 验潮站位置及基准站位置示意图Fig.1 Sketch map of the location of tide gauge station and reference station

2 计算方法

2.1 经验模态分解

经验模态分解法（EMD）对原始时间序列进行分解，将时间序列信号分解为一系列具有不同时间尺度的IMF分量（Intrinsic Mode Function）和1个最终余项，每个IMF分量需要满足2个条件：1）在全体数据序列中，极值点和过零点的个数必须相同或者最多相差1个；2）在任意一点，由局部极小值点组成的下包络线和局部极大值点确定的上包络线的算术平均值为0[7]。分解过程通过一个称为“筛选”的步骤来完成，对原始信号x（t）进行经验模态分解的基本步骤为：

1）求得原始信号x（t）的局部极大值和局部极小值，分别拟合上、下包络线；

2）分别计算上、下包络线的均值；

3）分别计算原始信号x（t）减去上、下包络线的均值；

4）判断是否满足IMF分量的2个筛选条件，若满足，则进入下一步；若不满足，则将步骤3）中结果返回步骤1）重新计算；

5）分解结果作为第i个IMF分量；

6）判断是否满足EMD分解终止条件，若满足转入步骤8），若不满足则转入步骤7）；

7）从原始信号中减去该层IMF分量作为新的原始信号返回步骤2），计算第i+1层IMF分量；

8）得到n个IMF分量和剩余分量。经分解得到一系列IMF分量后可表示为：

式中：rn（t）代表最终余项，表示信号的趋势成分；imfi（t）表示频率从高到低排列的n个IMF分量。

2.2 数据重构

根据经验模态分解过程可知，分解获得的n个IMF分量中，噪声信号对每个IMF分量的影响逐渐减小，信号对IMF分量的影响则不断增大。因此，为了获取准确的潮位数据，需要在m个IMF分量中确定潮位数据和噪声信号的分界IMF分量，以达到去除噪声信号的目的。基本步骤如下：首先，求取m个IMF分量与原序列的相关系数；其次，搜索求得的一系列相关系数中第1个取局部极小值的相关系数对应的IMF分量，其为噪声与信号的分界imfk分量；最后，将k及k之前的IMF分量重构为噪声序列，将k之后的IMF分量重构为周期项序列，通过重构被分解序列可以有效提取原序列的周期项[8]。

3 结果与分析

3.1 PPK解算结果

PPK数据后处理采用TBC解算软件，计算过程中均使用精密星历。由于PPK处理后获得水面高程的基面为GNSS椭球面，而潮位数据的基面为理论深度基准面，二者之间需要转换。利用车牛山站、油码头站、开山岛站转换关系得到各站基于理论深度基准面的PPK潮位，并和各长期站同步潮位数据共同绘制潮位过程线图。以车牛山站为例，从图2可以看出，车牛山站PPK验潮数据和车牛山站长期验潮站同期潮位变化趋势基本一致，但PPK验潮数据呈明显波动特征，这说明车牛山站PPK潮位数据中存在噪声序列。因此，为获取准确的潮位数据，必须对PPK潮位数据进行滤波处理，以去除潮位数据中的噪声序列。

图2 车牛山站长期潮位与PPK潮位过程线图Fig.2 Chart of long-term tide level and PPK tide level at Cheniushan station

3.2 经验模态分解与数据重构

通过经验模态分解车牛山站、油码头站、开山岛站PPK潮位，并以车牛山站为例说明经验模态分解效果，车牛山站2018年4月16—17日PPK潮位数据分解结果如图3所示。

图3 车牛山站PPK潮位经验模态分解结果Fig.3 Empirical mode decomposition results of PPK tidal level at Cheniushan station

从图3可以看出，基于潮位数据自身特点将信号自适应地分解为12个高频分量imf1～imf12、1个低频分量imf13和1个剩余分量。

分别求取各站分解后IMF分量和原始潮位信号的相关系数，计算结果见图4。从图4可以看出，车牛山站、开山岛站和油码头站imf1～imf12分量和原始潮位信号的相关性均小于0.1，相关性很差；车牛山站、开山岛站和油码头站imf13分量的相关系数分别为0.987、0.996和0.998，相关性很好。因此，将imf1～imf12分量作为噪声序列予以去除，将imf13分量作为周期项进行重构。潮位数据重构后，分别绘制各站PPK潮位和长期站同步潮位过程线，并以车牛山站为例说明，车牛山站潮位过程线见图5。由图5可知，去噪后的PPK潮位和长期站潮位趋势一致，且潮位信号波形清晰，这表明经验模态分解法能够有效滤除PPK潮位数据中噪声序列。

图4 各站IMF分量和原始数据相关系数图Fig.4 Graph of correlation coefficients between IMF components and raw data at each station

图5 车牛山站长期潮位和经验模态分解前后PPK潮位过程线图Fig.5 PPK tide level process diagram before and after long-term tidal level and empirical mode decomposition at Cheniushan Station

3.3 误差对比与分析

为定量说明经验模态分解法的去噪效果，分别将去噪前后的PPK潮位和同期长期站潮位的最大误差、平均绝对误差和均方根误差进行对比统计。由于车牛山站长期潮位时间间隔为5 min，油码头站和开山岛站均为10 min，因此按各长期潮位站的时间间隔提取重构后的PPK潮位数据。各潮位站的潮位精度统计结果见表2。

表2 经验模态分解前后PPK潮位和长期站潮位精度统计表Table 2 Statistical table of tidal level accuracy of PPK tidal level and long-term station before and after empirical mode decomposition cm

从统计结果可以看出，各验潮站最大误差、平均绝对误差和均方根误差均由大变小，如油码头站经验模态分解前后的最大误差分别为15.5 cm和9.7 cm、平均绝对误差分别为6.3 cm和2.9 cm、均方根误差分别为7.1 cm和4.6 cm。由此可见，经验模态分解能够有效滤除PPK潮位中的噪声信号，可将潮位精度从10 cm量级提高至5 cm左右。

此外，距基准站40 km的车牛山站、开山岛站经验模态分解后的平均绝对误差为5.5 cm、4.1 cm，而距基准站3.5 km的油码头站经验模态分解后的平均绝对误差仅为2.9 cm。由此可见，PPK潮位测量的精度和距基准站的距离呈负相关关系，即随基准站和验潮站距离的增大而减小。

4 结语

为提高PPK潮位测量精度，本文利用经验模态分解（EMD）对车牛山站、油码头站、开山岛站获得的PPK潮位时间序列进行分析、重构，剔除PPK潮位测量中的噪声序列，并将去噪后的PPK潮位和同期长期验潮站潮位进行对比。结果表明：

1）经验模态分解法能有效剔除PPK潮位数据中的高频噪声序列，有助于获取真实潮位数据。

2）PPK潮位和长期站潮位的平均绝对误差在10 cm以内，经验模态分解、重构后平均绝对误差在5 cm左右，PPK潮位数据可满足港口与航道工程的测量精度要求。

3）PPK潮位精度和基准站与验潮站之间距离呈负相关关系，即验潮站距基准站越远，PPK解算精度越低。