基于距离倒数加权的多站潮位改正方法可行性分析

徐丽君 程新平

(长江宜昌航道局 宜昌 443000)

0 引 言

随着海洋事业中对大面积海洋测绘工作发展的迫切需求，对海洋测绘的精度要求也越来越高[1].而海洋测绘最为重要的环节就是潮位的控制与改正，它直接影响海洋测绘的成果精度[2-3].传统的单站潮位改正和双站潮位改正已经无法满足大面积高精度海洋测绘的要求[4]，当前海洋测绘多采用三站和多站潮位改正方法.多站潮位改正方法包括分带分区法、距离倒数加权法及最小二乘法等，每种方法的适用条件和可操作性各有不同[5-7].目前主要沿用了水运工程测量规范中的分带法[8]，尽管三角分带法已使用多年而且被认为是一个比较理想的潮位改正方法，但其数学模型的建立一直是一个问题，过去作业中的图解法，由于存在明显的作图误差及分带误差，且计算繁琐，工作量繁重，已不能满足和适应海洋测绘自动化数据处理的要求.

为提高潮位改正数据处理的效率，简化作业步骤且保证其改正的精度，文中研究了基于距离倒数加权的多站潮位改正原理[9]，利用Matlab软件编写了基于距离倒数加权的多站潮位改正应用程序，对比其与分带分区法多站潮位改正方法特点的不同，结合两种方法的实验数据，对基于距离倒数加权的多站潮位改正方法进行可行性分析.

1 多站潮位改正方法技术原理

1.1 分带分区法改正模型

1.1.1两站水位分带改正法

图1为测区范围，若测区内A、B两站间的潮波传播是以一定的速度均匀传播的，即两站间的同相潮时和同相潮高的变化与其距离成比例.当测区位于A、B两站控制不到的C、D区时，可以根据A、B站的观测资料内插出C、D站的潮位数据进行潮位改正，见图2.

图1 测区范围

图2 内插法潮位改正

而两站间需分多少带，取决于从深度基准面起算的相同时刻海面的最大差值δh.水位分带数为[10-12]

(1)

式中：k为两潮位站间的分带数目；δh为测深读数精度，取0.1 m；δz为A、B两站相同时刻海面最大潮高差，简称高差，见图3.

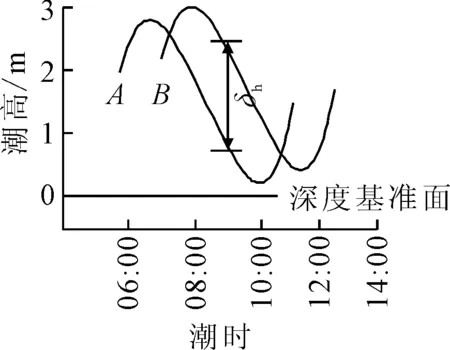
图3 最大潮高差示意图

设A、B两站间要分k带，则应内插出k-1条曲线.这就要在A、B曲线间所作的若干条同相潮波点连线上进行k等分，过对应的等分点连成圆滑曲线.图2中k=3，则中间内插2条曲线，在各短在线按3等分进行等分.

1.1.2三站水位分带改正法(又称三角分带法)

与两站水位分带改正法类似，为了加强潮波传播垂直方向的控制，需要采用三站水位分带改正法，见图4.该方法主要针对测量面积较大，且海面较为开阔的区域.其基本原理为：先进行两两站之间的水位分带，在计算分带时应注意使其闭合.这样在每一带的两端都有一条水位曲线控制.如在C带，一端为C站的水位曲线，另一端为A、B边的第2带的水位曲线.若两端水位曲线同一时刻的δh大于测深精度δz，则该带还需分区[13].图4中分区数为3，各区分别为C0、C1和C2.C1水位曲线就是由C站和AB站的第2带的水位曲线内插获得的.

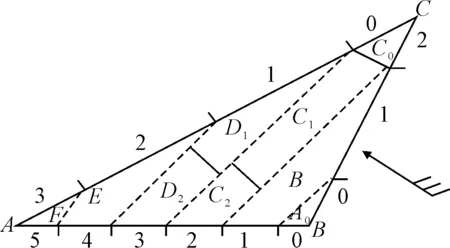
图4 三站分带示意图

1.2 基于距离倒数加权的多站潮位改正方法

1.2.1二步内插法三站潮位改正

设A1、A2、A3三个潮位站某时刻的潮位分别为Z1、Z2、Z3，求P点的潮位，见图5.

由A1、A2、A3和P的坐标，可联解求得A2、A3与A1P两个直线方程，得A4的坐标，在直线A2、A3上以这两点潮位按距离内插得到A4的潮位，在直线A1A4上，以A1A4的潮位线性内插求得测点P的潮位[14]，即

Zp=(Z4-Z1)/SA1A4×SA1P+Z1

(2)

式中：SA1A4、SA1P分别为A4与A1、A1与P的距离；ZP为P点的潮位.

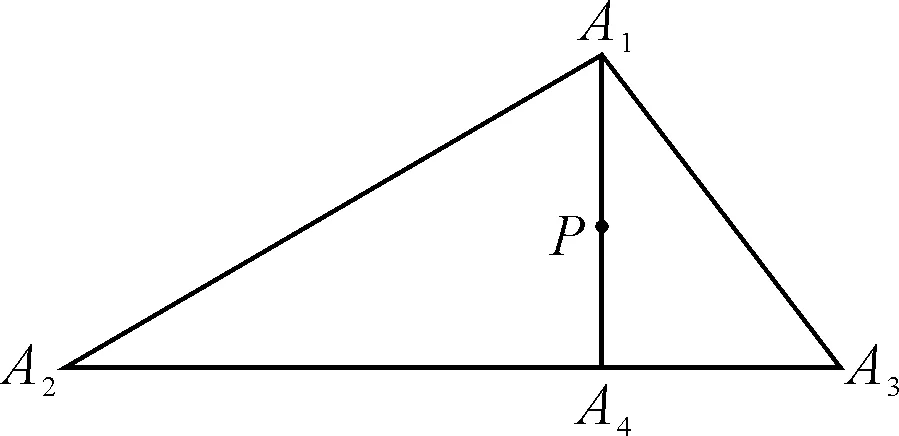
图5 二步内插法示意图

1.2.2基于距离倒数加权的多站潮位改正

依据二步内插法模型类推，由于P点潮位与其距潮位站的距离比例，距离越远的潮位站对P点潮位的影响越小，反之亦然.根据现代测量平差理论[15]，基于距离倒数加权的多站潮位改正数学模型为图6.

图6 基于距离倒数加权的多站潮位改正数学模型示意图

(3)

式中：Z1,Z2,Z3,…,Zi和ZP分别为A1,A2,A3,…Ai和P点的瞬时潮位值，SA1P,SA2P,SA3P,…,SAiP分别为P点与潮位站A1,A2,A3,…,Ai的距离.

2 基于距离倒数加权的多站潮位改正程序实现

根据距离倒数加权的多站潮位改正原理数学模型结合实际生产中水位文件及测深数据文件格式，利用Matlab编写了基于距离倒数加权的多站潮位改正应用程序，并采用生产实例数据验证其可行性.

水深文件格式依据HYPACK综合测量软件校对水深后生成的“.EDT”文件.潮位文件借鉴HYPACK软件的潮位文件“.tdx”文件格式，在表头加入各个潮位站坐标信息，见图7.

图7 潮位文件格式

水位改正采用逐点改正法，即根据各验潮站的位置信息、各验潮站的瞬时潮位、测点的瞬时位置信息，利用基于距离倒数加权的多站潮位改正数学模型(式(3))计算测点的瞬时潮位.以利用5个验潮站潮位数据进行多站潮位改正为例，程序代码如下.

for i=1:ds_1

if(Time_t

Tide_t_1=Tide_1(i,1)-(Tide_1(i,1)-Tide_1(i-1,1))*

(Time_1(i,1)-Time_t)/(Time_1(i,1)-Time_1(i-1,1));

LL_1=sqrt((XX_1-X_t)2+(YY_1-Y_t)2);

break;

end

end

…

…

…

for i=1:ds_5

if(Time_t

Tide_t_5=Tide_5(i,1)-(Tide_5(i,1)-Tide_5(i-1,1))*

(Time_5(i,1)-Time_t)/(Time_5(i,1)-Time_5(i-1,1));

LL_5=sqrt((XX_5-X_t)2+(YY_5-Y_t)2);

break;

end

end

Tide_c=(Tide_t_1/LL_1+Tide_t_2/LL_2+Tide_t_3/LL_3+Tide_t_4/LL_4

+Tide_t_5/LL_5)/(1/LL_1+1/LL_2+1/LL_3+1/LL_4+1/LL_5);

3 实例数据分析

以长江口南附近感潮河段水域为例，该河段位于长江口南港河段下段，附近有长期验潮站8个，分别为三甲港、九段沙、中浚、南槽东、鸡骨礁、牛皮礁、大戢山、芦潮港.属非正规半日浅海潮.一日内两涨两落，一涨一落平均历时12 h25 min，日潮不等现象明显.

通过收集测量期间各个验潮站的潮位资料，比较分析长期验潮站潮位资料的涨落潮关系、高低潮关系及平潮出现时间等情况，对测区采用潮位分带法进行水位改正.其中在中浚至南槽东段分4带，南槽东至大戢山段分4带，大戢山至芦潮港段分7带，分带分区示意图见图8.

图8 潮位改正分带示意图

以九段沙、中浚、牛皮礁、南槽东、大戢山、芦潮港6个长期验潮站数据为潮位数据，采用基于距离倒数加权的多站潮位改正应用程序对测深数据进行逐点潮位改正.

实例数据依照JTS 131-2012《水运工程测量规范》要求采用常规双站分带法潮位改正方法，得到的水深值作为参考值，采用基于距离倒数加权的多站潮位改正方法应用程序对测深数据进行潮位改正，将最终得到的水深值与双站分带法得到的水深值进行比对分析.

由于参考值是采用双站分带法所得，而非多站分带分区法，而基于距离倒数加权法是多站潮位改正，因此采用带状方式选取中浚、南槽东、大戢山三个长期验潮站连线的带状区域数据作为比对数据.比对结果统计见表1.

表1 潮位改正精度统计表

采用基于距离倒数加权的多站潮位改正方法进行潮位改正结果与常规的分带法潮位改正结果，符合性很好，完全能达到现有海洋测绘精度的要求.

4 结 束 语

分带分区法是现在针对大面积海洋测绘工作最常用的方法，经过多年的应用，早已被证明该方法精度是可靠的.优点是该方法考虑到了潮时差因素对潮位改正的影响，原理相对严谨；缺点是忽略了相邻两带间存在0.1 m的裂隙差影响，且实现过程繁琐.

基于距离倒数加权法潮位改正避免了潮位分带法的裂隙差问题，该方法程序化操作简单，并且通过实例数据验证结果也表明了该方法与常规分带法潮位改正所得结果吻合性很高.因此，基于距离倒数加权的多站潮位改正方法精度可靠，程序化处理效率高，完全能够满足现行海洋测绘规范的要求.